Manthan, Codefest 19 (open for everyone, rated, Div. 1 + Div. 2)-E. Let Them Slide-思维+数据结构
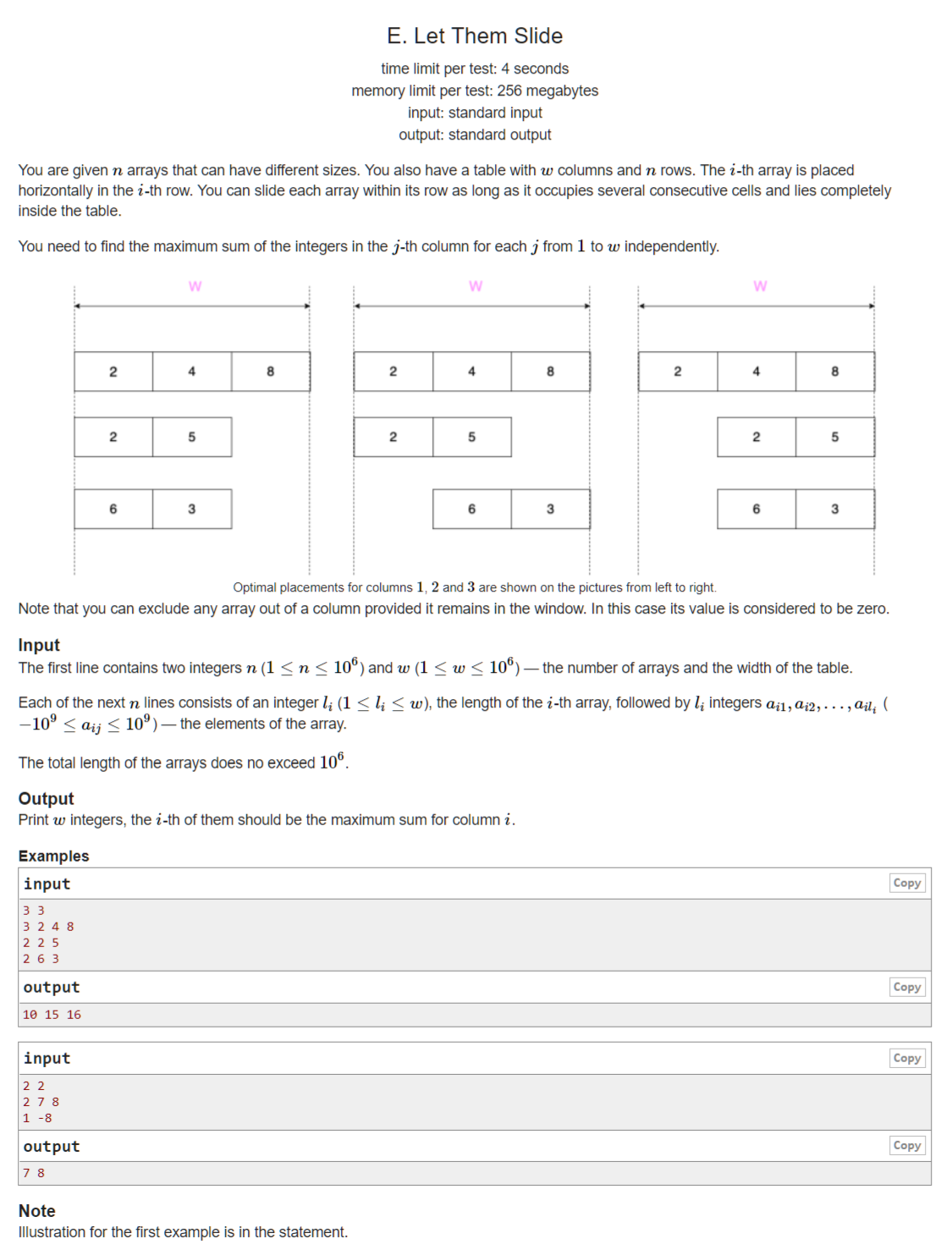
【Problem Description】
(n imes w)的方格中,每一行有(cnt_i)个数字,每一行的数字都连续的放在一起,但是可以任意的平移。问每一列的最大和为多少。
【Solution】
最直观的想法是对于每一列(j),计算出每一行中的一个区间最大值,此区间长度为(len=w-cnt+1)。即能对第(j)列产生贡献的区间范围为([j-len+1,j])。区间最大值可以很容易的用单调栈实现,但是(n,wle10^6),而此方法的复杂度为(O(ncdot w))。所以不可行。
根据题目条件所有数组总长度不超过(10^6)。所以可以换个角度,考虑每一行的第(j)个数能对哪些列产生贡献。可以发现对于第(j)个数来说,能产生贡献的列的范围为([j,w-cnt+j])。所以可以将所有数,按列分类,对于每一行维护一个(set),存储所有合法范围内的值,每次转移列时,将不合法的值从(set)中移除即可。此时对第(j)列的贡献就是(set)中的最大值。
【Code】
/*
* @Author: Simon
* @Date: 2019-08-27 13:32:39
* @Last Modified by: Simon
* @Last Modified time: 2019-08-27 13:57:34
*/
#include<bits/stdc++.h>
using namespace std;
typedef int Int;
#define int long long
#define INF 0x3f3f3f3f
#define maxn 1000005
int ans[maxn];
vector<pair<int,int> >add[maxn],remv[maxn];
multiset<int>s[maxn];
Int main(){
#ifndef ONLINE_JUDGE
//freopen("input.in","r",stdin);
//freopen("output.out","w",stdout);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
int n,w;cin>>n>>w;
for(int i=1;i<=n;i++){
int cnt;cin>>cnt;
for(int j=1;j<=cnt;j++){
int x;cin>>x;
add[j].push_back({x,i}); //按列分类,起点
remv[w-cnt+j].push_back({x,i}); //终点
}
if(cnt<w){
add[1].push_back({0,i});
remv[w-cnt].push_back({0,i});
add[cnt+1].push_back({0,i});
remv[w].push_back({0,i});
}
}
for(int j=1;j<=w;j++){
for(auto v:add[j]){
int idx=v.second,val=v.first;
ans[j]-=s[idx].empty()?0:*s[idx].rbegin();
s[idx].insert(val);
ans[j]+=*s[idx].rbegin();
}
if(j<w){
ans[j + 1] = ans[j];
for(auto v:remv[j]){ //remv[j]表示这些数对第j列有贡献,对j+1列就没有贡献了,所以统计第j+1列的最大值时,需要将这些数移除。
int idx=v.second,val=v.first;
ans[j+1]-=*s[idx].rbegin();
s[idx].erase(s[idx].find(val));
ans[j+1]+=s[idx].empty()?0:*s[idx].rbegin();
}
}
}
for(int i=1;i<=w;i++) cout<<ans[i]<<"
"[i==w];
#ifndef ONLINE_JUDGE
cout<<endl;system("pause");
#endif
return 0;
}