RSA

同余：给定一个正整数m，如果两个整数a和b满足(a-b)能够被m整除，即 (a-b)/m 得到一个整数，

　　　　那么就称整数a b对模m同余，记做a ≡ b( mod n )

RSA算法的参数构成：

　　1)选择两个大素数p、q；

　　2)计算n，n = pq和n的欧拉定理的值，ψ(n) = (p-1)(q-1)

　　3)随机选择公钥e，e只需要满足1<e<ψ(n)，并且e和ψ(n)互素，(e, ψ(n)) = 1

　　4)计算私钥d，满足ed ≡ 1( mod ψ(n))

公钥(e，n)，私钥(d，n)

最基本的RSA算法，很容易受到选择密文攻击，所以一帮可以采用最佳对称加密填充(OAEP)来解决。

　　这样就切断了攻击者，直接利用密文来测试明文的途径。

CRT，Chinese Remander Theorem是一种对模幂运算速度进行优化的算法。

在计算模幂的时候，可以分为两步：

1)CRT  keysetup

　　input    p(first prime  modulus  factors)，q(second  prime  modulus  factors)，d(私钥 secret exponent)

　　output dp，dq，qinv；

　　　　流程：qinv = 1/q mod p；

　　　　　　　dp = d mod (p-1)；

　　　　　　　dq = d mod (q-1)；

2)CRT  Modular Exponent

　　input   msg，  p，  q，  qinv，  dp，  dq

　　output  c

　　　　流程：mp = msg^p mod p；

　　　　　　　mq = msg^q mod q；

　　　　　　    i = mp^dp mod p；

　　　　　　    j = mq^dq mod q；

　　　　　　    j' = j mod p；

　　　　　　    k = (i - j') mod p；

　　　　　　    L = (k*qinv) mod p；

　　　　　　　 s = L*q

　　　　　　　 c = s+j

由于公钥e的一般范围都比较小，openssl的默认值是3-64之间，所以加密运算和signature，一般是不用crt加速的。

这样：公钥一般指：(n,e)

　　　私钥一般指：(n,d)  (p,q,dp,dq,qinv)

RSA的key_generation函数：包括1)选择公钥指数e，2)内部产生factors，p，q，n，3)计算私钥指数d

　　input包括：

　　　　1) k，length of modulus n in bits，(k = 1024+256s)

　　　　2) e的长度，2<=e<=2^k-160 (e的长度为零，表示内部自己randomize)

　　　　3) hash function, random_seed，TRNG function

　　output包括：

　　　　1)公钥(n, e)

　　　　2)私钥(n, d)以及(p,q,dp,dq,qinv)

公钥e一般可以使用固定值也可以使用随机值，

　　固定值，一般包括2，3，17，2¹⁷+1(65537)

　　随机值一般要求，e的最高位和最低位都为1，并且，2<=e<2^k-160 k为modulus n的bits

RSA的应用可以分为加解密primitives和签名验签primitives

　　1) Encryption/Decryption primitives，

　　　　RSAEP((n,e), m)

　　　　输入：   (n,e) RSA公钥

　　　　　　　　m    message，范围在0 - n-1之间，否则报错

　　　　输出：c    ciphertext，范围在0 - n-1之间，

　　　　步骤：1) 判断m的范围是否在0 - n-1之间，否则报错

　　　　　　　2) c = m^emod n

　　　　　　　3) 输出c

　　　　RSADP(K,c)

　　　　输入：K--------(n, d)

　　　　　　　　　　 (p,q,dp,dq,qinv)

　　　　　　　c    ciphertext，在0 - n-1之间

　　　　输出：m    message，范围在0 - n-1之间

　　　　步骤：crt_exp或mod_exp算法

　　2)Signature/Verifiaction primitives，

　　　　RSASP1(K, m)

　　　　输入：  K---------一对密钥(n,d)

　　　　　　　　 ---------CRT的密钥序列(p,q,dp,dq,qinv)

　　　　　　　  m   message介于0 - n-1之间

　　　　输出：  s   signature介于0 - n-1之间

　　　　步骤：   1)判断message的范围在0 - n-1之间，

　　　　　　　　2)进行crt_exp, mod_exp的计算。

　　　　RSAVP1((n,e), s)

　　　　输入：   (n,e) RSA公钥

　　　　　　　　s signature介于0 - n-1之间

　　　　输出： m   message 基于0-n-1之间

　　　　步骤：m = s^emodn

　　　　在签名验签中必须保证密钥对是正确的。这是一个前提条件

在PKCS1的标准中：

encryption scheme可以分为RSAES-OAEP和RSAES-PKCS1-v1.5

　　RSAES-OAEP的步骤：

　　　　RSAES-OAEP-ENCRYPT

　　　　

　　　　1) 首先检查原始字符串的长度是否超过sha运算的最大支持长度；

　　　　　　检查mLen的长度是否<= k -2hLen -2

　　　　2) EME-OAEP encoding，产生EM(Encoding message)

　　　　　　

　　　　　　其中seed为随机数，lHash，不同的hash算法，初始值不同：

　　　　　　　　

　　　　3) RSA encryption primitive

　　　　RSAES-OAEP-DECRYPT(K, C, L)步骤：

　　　　 

　　　　1)长度检查，原始字符串的长度必须小于SHA运算的最大值；

　　　　　　　　　　如果密文C不是modulus的比特数，输出decryption error

　　　　　　　　　　如果k < 2hLen + 2，输出decryption error

　　　　2) RSA decryption

　　　　3) EME-OAEP decoding

　　　　　　

　　RSAES-PKCS1-V1_5-Encrypt((n,e) M)

　　　　　　Encryption步骤：

　　　　　　　　

　　　　　　　　1) length check，mLen > k-11

　　　　　　　　2) EME_PKCS1-v1_5 encoding，

　　　　　　　　3) RSA encryption

　　　　　　Decryption步骤：

　　　　　　　　

　　　　　　　　1) length check，如果k<11或者C不是k bit长度

　　　　　　　　2) RSA decryption

　　　　　　　　3) EME-PKCS1-v1_5 decoding

Signature和Verification的流程有：RSASSA-PSS和RSASSA-PKCS1-v1_5

　　　　　　PSS：RSASSA-PSS-SIGN(K, M)

　　　　　　　　

　　　　　　　　步骤：    EMSA-PSS encoding

　　　　　　　　　　　　 RSA signature

　　　　　　　　RSASSA-PSS-VERIFY ((n,e), M, S)

　　　　　　　　

　　　　　　　　步骤：   Length checking

　　　　　　　　　　　　RSA verification

　　　　　　　　　　　　EMSA-PSS decoding

　　RSASSA-PKCS1-v1_5只是encoding和decoding的方式不同。

具体的encoding方式，见http://www.cnblogs.com/-9-8/p/7997965.html  

RSA-X9.31 1998中的Signature和Verification流程：

　　　　

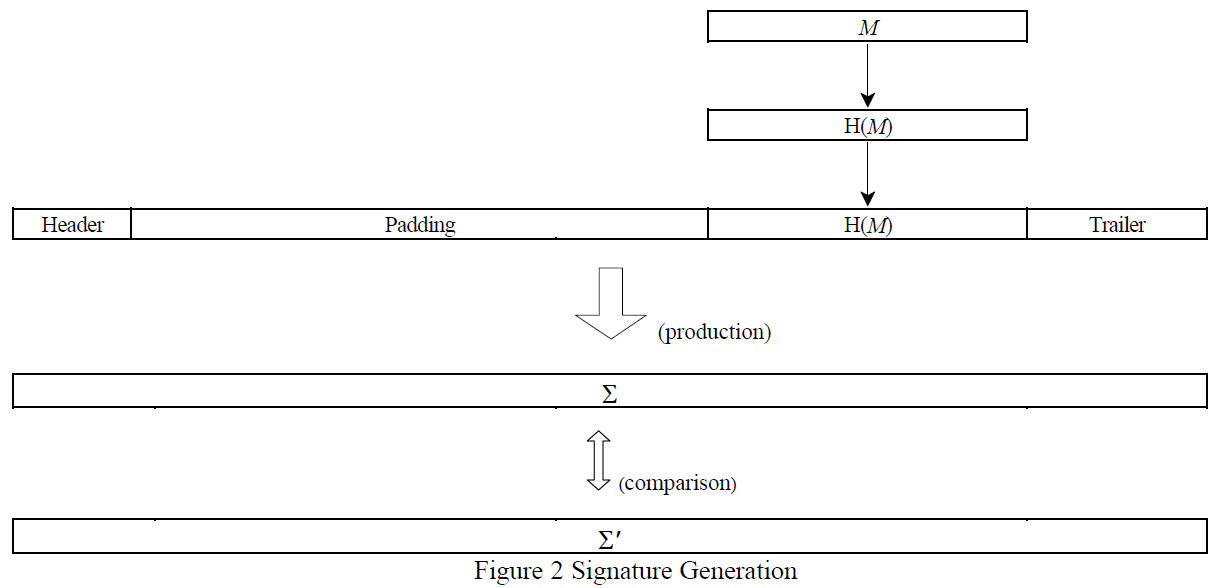
verification流程：

　　　　

　　　　

关于RSA的一个很好的网页

https://www.di-mgt.com.au/rsa_alg.html