zoukankan html css js c++ java

树状数组

树状数组基础

树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&区间求和.

另外一个拥有类似功能的是线段树.

具体区别和联系如下：

1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.

2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.

3.树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作，其代码效率远高于线段树。

上面出现了一个新名词:lowbit.其实lowbit(x)就是求x最低位的1;

下面加图进行解释

对于一般的二叉树,我们是这样画的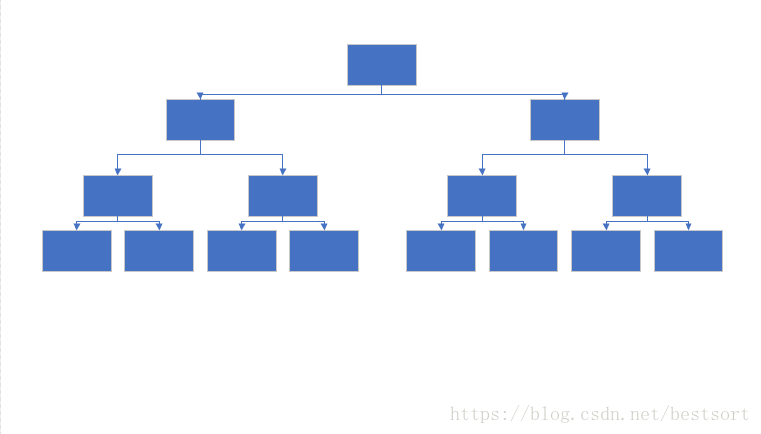

把位置稍微移动一下，我们就可以得到树状数组的画法

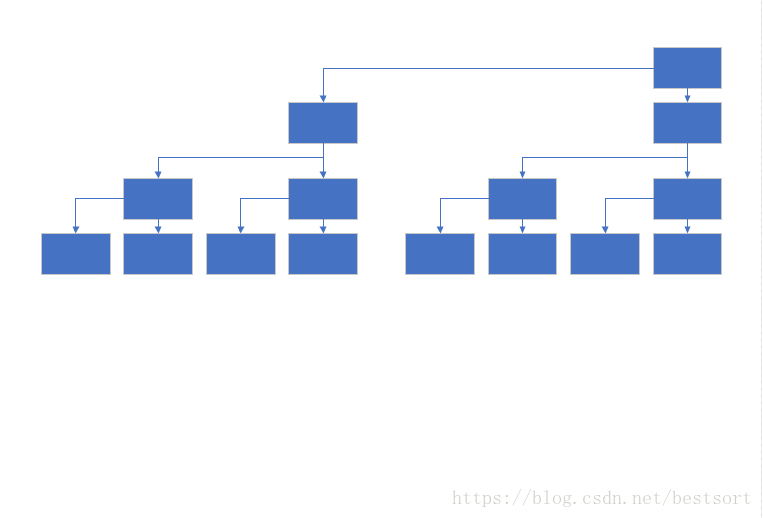
上图其实是求和之后的数组,原数组和求和数组的对照关系如下,其中a数组是原数组,c数组是求和后的数组

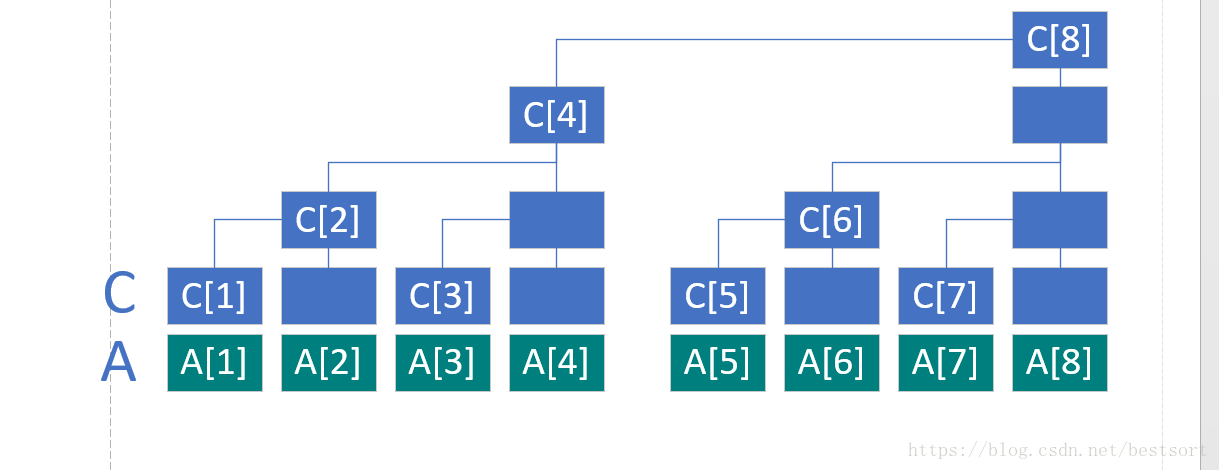
C[i]代表子树的叶子结点的权值之和

如图可以知道

C[1]=A[1];

C[2]=A[1]+A[2];

C[3]=A[3];

C[4]=A[1]+A[2]+A[3]+A[4];

C[5]=A[5];

C[6]=A[5]+A[6];

C[7]=A[7];

C[8]=A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

再将其转化为二进制看一下:

C[1] = C[0001] = A[1];

C[2] = C[0010] = A[1]+A[2];

C[3] = C[0011] = A[3];

C[4] = C[0100] = A[1]+A[2]+A[3]+A[4];

C[5] = C[0101] = A[5];

C[6] = C[0110] = A[5]+A[6];

C[7] = C[0111] = A[7];

C[8] = C[1000] = A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7]+A[8];

对照式子可以发现 C[i]=A[i-2^k+1]+A[i-2^k+2]+......A[i]; （k为i的二进制中从最低位到高位连续零的长度）例如i=8(1000)时，k=3;

C[8] = A[8-2^3+1]+A[8-2^3+2]+......+A[8]

即为上面列出的式子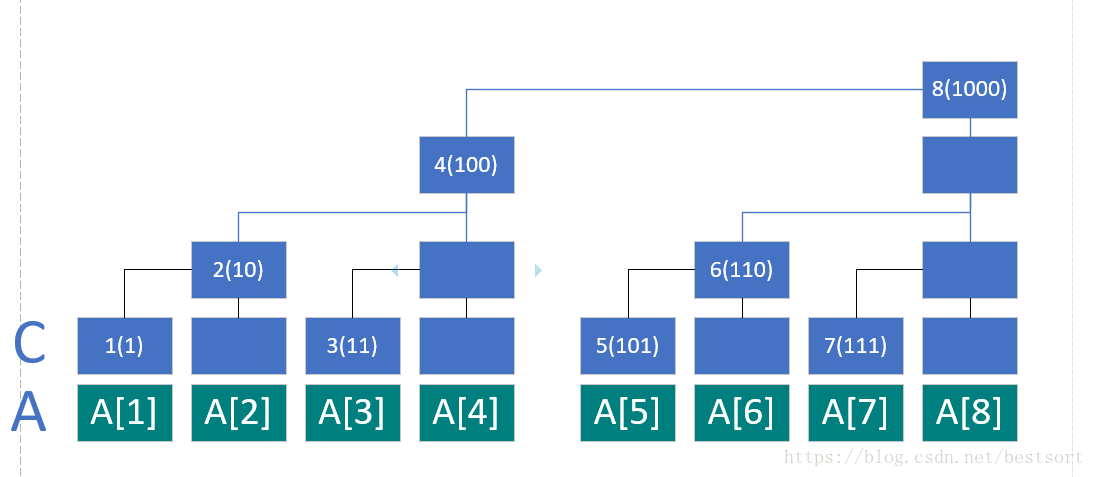

现在我们返回到lowbit中来

其实不难看出lowbit(i)便是上面的2^k

因为2^k后面一定有k个0

比如说2^5==>100000

正好是i最低位的1加上后缀0所得的值

开篇就说了,lowbit(x)是取出x的最低位1;具体操作为

int lowbit(int x)
{
    return x&(-x);
}

我们知道,对于一个数的负数就等于对这个数取反+1

以二进制数11010为例:11010的补码为00101,加1后为00110,两者相与便是最低位的1

其实很好理解,补码和原码必然相反,所以原码有0的部位补码全是1,补码再+1之后由于进位那么最末尾的1和原码

最右边的1一定是同一个位置(当遇到第一个1的时候补码此位为0,由于前面会进一位,所以此位会变为1)

所以我们只需要进行a&(-a)就可以取出最低位的1了

会了lowbit,我们就可以进行区间查询和单点更新了!!!

单点更新

其实我个人觉得这步骤就是相当于线段树从叶子节点开始向上建树或者修改父亲节点的值

只不过这里用lowbit进行实现更加简洁

void add(int p,int x) // 给p位置增加x
{
    while (p<=n)   // n是树状数组的大小
    {
        C[p] += x;
        p += p & -p;
    }
}

区间查询、前缀和

这个操作其实就是单点更新的逆操作，我们从父亲节点开始向下查询

int lowbit(int x)
{
    return x&(-x);
}



void updata(int p,int x) // 给p位置增加x
{
    while (p<=n)   // n是树状数组的大小
    {
        C[p] += x;
        p += lowbit(p);
    }
}

int getsum(int p) //查询[1-p]的前缀和
{
    int res = 0;
    while (p)
    {
        res += C[p];
        p -= lowbit(p);
    }
    return res;
}

int range_ask(int l,int r) // 求区间和
{
    return getsum(r)-getsum(l-1);
}

区间修改+单点查询

通过“差分”（就是记录数组中每个元素与前一个元素的差），可以把这个问题转化为问题1。

查询

$a [i] = \sum_{j = 1}^{i} d [j]$

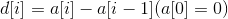
修改

当给区间 $[l,r]$ 加上x的时候， $a[l]$ 与前一个元素 $a[l-1]$ 的差增加了x， $a[r+1]$ 与 $a[r]$ 的差减少了x。根据 $d[i]$ 数组的定义，只需给 $a[l]$ 加上 x, 给 $a[r+1]$ 减去x即可

int lowbit(int x)
{
    return x&(-x);
}

void updata_first(int p,int x) // 给p位置增加x
{
    while (p<=n)   // n是树状数组的大小
    {
        C[p] += x;
        p += lowbit(p);
    }
}

int getsum(int p) //查询A[p]
{
    int res = 0;
    while (p)
    {
        res += C[p];
        p -= lowbit(p);
    }
    return res;
}

int range_updata_first(int l,int r,int x) // 区间修改
{
    updata_first(l,x);
    updata_first(r+1,-x);
}

int main(){
    cin>>n;
    for(int i = 1; i <= n; i++){
        cin>>a[i];
        updata_first(i,a[i]-a[i-1]);   //输入初值的时候，也相当于更新了值
    }
    range_updata_first(1,4,3);
    for (int i=1;i<=n;i++)
        printf("%d
",getsum(i));
    return 0;
}

3. 区间修改 + 区间查询

这是最常用的部分，也是用线段树写着最麻烦的部分——但是现在我们有了树状数组！

怎么求呢？我们基于问题2的“差分”思路，考虑一下如何在问题2构建的树状数组中求前缀和：

位置p的前缀和 =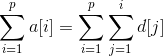

在等式最右侧的式子中

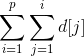
d[1]被用了p次，d[2]被用了p-1次……那么我们可以写出：

位置p的前缀和 =

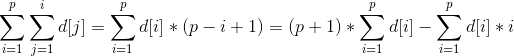
那么我们可以维护两个数组的前缀和：
一个数组是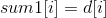

另一个数组是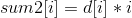

查询
位置p的前缀和即：数组中p的前缀和 - sum2数组中p的前缀和。

区间[l, r]的和即：位置r的前缀和 - 位置l的前缀和。

修改
对于sum1数组的修改同问题2中对d数组的修改。

对于sum2数组的修改也类似，我们给 sum2[l] 加上 l * x，给 sum2[r + 1] 减去 (r + 1) * x。

int n,m;
int a[MAXN] = {0};
int sum1[MAXN];
int sum2[MAXN];

int lowbit(int x)
{
    return x & (-x);
}

void updata_second(int i,int k)  
{
    int x = i;
    while (i<=n)
    {
        sum1[i] += k;
        sum2[i] += k*(x-1);
        i += lowbit(i);
    }
}

void range_updata_second(int l,int r,int k)
{
    updata_second(l,k);
    updata_second(r+1,-k);
}


int getsum(int i) //前缀和
{
    int res = 0;
    int x = i;
    while (i)
    {
        res += x*sum1[i]-sum2[i];
        i -= lowbit(i);
    }
    return res;
}

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        updata_second(i,a[i]-a[i-1]);
    }
    range_updata_second(1,3,5);
    for (int i=1;i<=n;i++)
        printf("%d
",getsum(i));
    return 0;
}

4. 二维树状数组

我们已经学会了对于序列的常用操作，那么我们不由得想到（谁会想到啊喂）……能不能把类似的操作应用到矩阵上呢？这时候我们就要写二维树状数组了！

在一维树状数组中，tree[x]（树状数组中的那个“数组”）记录的是右端点为x、长度为lowbit(x)的区间的区间和。
那么在二维树状数组中，可以类似地定义tree[x][y]记录的是右下角为(x, y)，高为lowbit(x), 宽为 lowbit(y)的区间的区间和。

单点修改 + 区间查询

int n;
int a[MAXN][MAXN];
int tree[MAXN][MAXN];

int lowbit(int x)
{
    return x & (-x);
}

void updata(int x,int y,int z) // 将点(x,y)加上z
{
    int memo_y = y;
    while (x<=n)
    {
        y = memo_y;
        while (y<=n)
        {
            tree[x][y] += z;
            y += lowbit(y);
        }
        x += lowbit(x);
    }
}

int getsum(int x,int y) // 左上角为(1,1) 右下角为(x,y)的矩阵和
{
    int res = 0;
    int memo_y = y;
    while (x)
    {
        y = memo_y;
        while (y)
        {
            res += tree[x][y];
            y -= lowbit(y);
        }
        x -= lowbit(x);
    }
    return res;
}

int main()
{
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=n;j++)
        {
            scanf("%d",&a[i][j]);
            updata(i,j,a[i][j]);
        }
    }
    int sum = getsum(2,2);
    printf("%d
",sum);
    return 0;
}

区间修改 + 单点查询

我们对于一维数组进行差分，是为了使差分数组前缀和等于原数组对应位置的元素。

那么如何对二维数组进行差分呢？可以针对二维前缀和的求法来设计方案。

二维前缀和：

$sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+a[i][j]$

那么我们可以令差分数组 $d[i][j]$ 表示 $a[i][j]$ 与 $a[i-1][j]+a[i][j-1]-a[i-1][j-1]$ 的差。

当我们想要将一个矩阵加上x时，怎么做呢？
下面是给最中间的3*3矩阵加上x时，差分数组的变化：

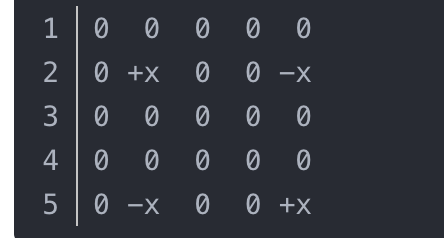
这样给修改差分，造成的效果就是：

int n;
int a[MAXN][MAXN]={0};
int tree[MAXN][MAXN];

int lowbit(int x)
{
    return x & (-x);
}

void updata(int x,int y,int z) // 将点(x,y)加上z
{
    int memo_y = y;
    while (x<=n)
    {
        y = memo_y;
        while (y<=n)
        {
            tree[x][y] += z;
            y += lowbit(y);
        }
        x += lowbit(x);
    }
}

void range_updata(int xa,int ya,int xb,int yb,int z) // 区间修改
{
    updata(xa,ya,z);
    updata(xa,yb+1,-z);
    updata(xb+1,ya,-z);
    updata(xb+1,yb+1,z);
}


int getsum(int x,int y) // 求a[x][y]的值
{
    int res = 0;
    int memo_y = y;
    while (x)
    {
        y = memo_y;
        while (y)
        {
            res += tree[x][y];
            y -= lowbit(y);
        }
        x -= lowbit(x);
    }
    return res;
}

int main()
{
    freopen("../in.txt","r",stdin);
    scanf("%d",&n);
    for (int i=1;i<=n;i++)
    {
        for (int j=1;j<=n;j++)
        {
            scanf("%d",&a[i][j]);
            updata(i,j,a[i][j]-a[i-1][j]-a[i][j-1]+a[i-1][j-1]);
        }
    }
    range_updata(1,1,3,3,1);
    for (int i=1;i<=3;i++)
    {
        for (int j=1;j<=3;j++)
            printf("%d
",getsum(i,j));
    }
    return 0;
}

区间修改 + 区间查询

类比之前一维数组的区间修改区间查询，下面这个式子表示的是点(x, y)的二维前缀和：

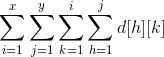
(d[h][k]为点(h, k)对应的“二维差分”(同上题))

这个式子炒鸡复杂( $O(n^4)$ 复杂度！)，但利用树状数组，我们可以把它优化到 $O(log_2 n)$ ！

首先，类比一维数组，统计一下每个 $d[h][k]$ 出现过多少次。 $d[1][1]$ 出现了 $x*y$ 次， $d[1][2]$ 出现了 $x*(y-1)$ 次…… $d[h][k]$ 出现了 $(x-h+1)*(y-k+1)$ 次。

那么这个式子就可以写成：

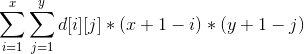
把这个式子展开，就得到：

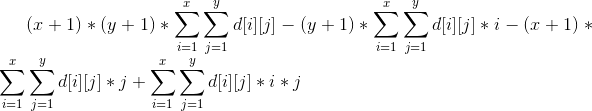
那么我们要开四个树状数组，分别维护：

$d[i][j]$ , $d[i][j]*i$ , $d[i][j]*j$ , $d[i][j]*i*j$

void add(ll x, ll y, ll z){
    for(int X = x; X <= n; X += X & -X)
        for(int Y = y; Y <= m; Y += Y & -Y){
            t1[X][Y] += z;
            t2[X][Y] += z * x;
            t3[X][Y] += z * y;
            t4[X][Y] += z * x * y;
        }
}
void range_add(ll xa, ll ya, ll xb, ll yb, ll z){ //(xa, ya) 到 (xb, yb) 的矩形
    add(xa, ya, z);
    add(xa, yb + 1, -z);
    add(xb + 1, ya, -z);
    add(xb + 1, yb + 1, z);
}
ll ask(ll x, ll y){
    ll res = 0;
    for(int i = x; i; i -= i & -i)
        for(int j = y; j; j -= j & -j)
            res += (x + 1) * (y + 1) * t1[i][j]
                - (y + 1) * t2[i][j]
                - (x + 1) * t3[i][j]
                + t4[i][j];
    return res;
}
ll range_ask(ll xa, ll ya, ll xb, ll yb){
    return ask(xb, yb) - ask(xb, ya - 1) - ask(xa - 1, yb) + ask(xa - 1, ya - 1);
}

参考：https://www.cnblogs.com/RabbitHu/p/BIT.html

$a [i] = \sum_{j = 1}^{i} d [j]$

查看全文

相关阅读:
django–url
SQLServer-镜像配置
 linux-阿里云ECS部署PPTP（centos)
linux- svn服务器
 python(7)– 类的反射
 python(7)–类的多态实现
 python(6)-shutil模块
 python(6)-执行shell命令
 python(6)-类
 nagios–配置文件

原文地址：https://www.cnblogs.com/-Ackerman/p/11264510.html