题目链接:https://cn.vjudge.net/contest/318888#problem/H
题意:
求两个子串的字符串的最长公共子串
思路:
"最长公共子串"解法(摘自罗穗骞的国家集训队论文):
字符串的任何一个子串都是这个字符串的某个后缀的前缀。 求A和B的最长公共子串等价于求A的后缀和B的后缀的最长公共前缀的最大值。如果枚举A
和B的所有的后缀, 那么这样做显然效率低下。 由于要计算A的后缀和B的后缀的最长公共前缀, 所以先将第二个字符串写在第一个字符串后面, 中间用一个没有出现过的字符隔开,再求这个新的字符串的后缀数组。观察一下,看看能不能从这个新的字符串的后缀数组中找到一些规律。以A=“ aaaba”, B=“ abaa” 为例,如图所示。
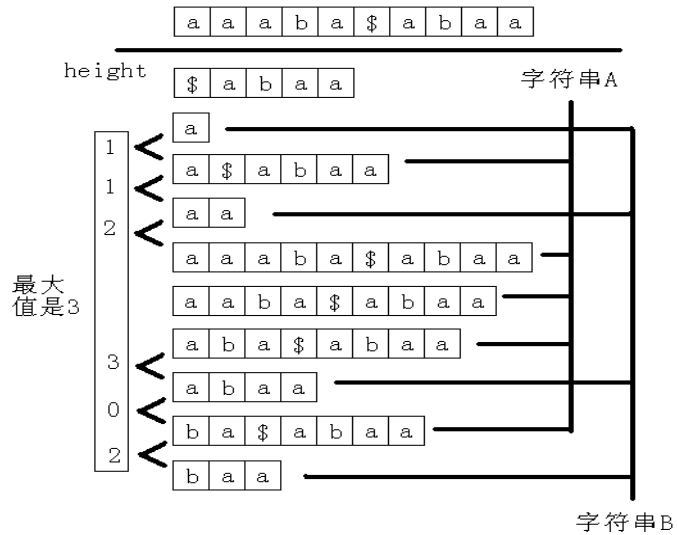
那么是不是所有的height值中的最大值就是答案呢?不一定!有可能这两个后缀是在同一个字符串中的,所以实际上只有当 suffix(sa[i-1])和suffix(sa[i])不是同一个字符串中的两个后缀时, height[i]才是满足条件的。而这其中的最大值就是答案。 记字符串A和字符串B的长度分别为|A|和|B|。 求新的字符串的后缀数组和height数组的时间是O(|A|+|B|),然后求排名相邻但原来不在同一个字符串中的两个后缀的 height 值的最大值,时间也是O(|A|+|B|),所以整个做法的时间复杂度为O(|A|+|B|)。时间复杂度已经取到下限,由此看出,这是一个非常优秀的算法。
ps:因为两个字符合成一个字符时,中间(位置k)会用一个没有出现过的字符隔开,所以判断两个后缀是不是同一个字符串可以借助这个位置k
即当(sa[i]-k)*(sa[i-1]-k)<0时,两个后缀属于不同的字符串,此题求乘积时可能会爆int,注意一下即可
1 #include <stdio.h> 2 #include <iostream> 3 #include <algorithm> 4 #include <string.h> 5 #include <stdlib.h> 6 #include <math.h> 7 #include <queue> 8 #include <set> 9 10 #define INF 0x3f3f3f3f 11 #define pii pair<int,int> 12 #define LL long long 13 using namespace std; 14 typedef unsigned long long ull; 15 const int MAXN = 200005; 16 17 int wa[MAXN], wb[MAXN], wv[MAXN], ws_[MAXN]; 18 void Suffix(int *r, int *sa, int n, int m) 19 { 20 int i, j, k, *x = wa, *y = wb, *t; 21 for(i = 0; i < m; ++i) ws_[i] = 0; 22 for(i = 0; i < n; ++i) ws_[x[i] = r[i]]++; 23 for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1]; 24 for(i = n - 1; i >= 0; --i) sa[--ws_[x[i]]] = i; 25 for(j = 1, k = 1; k < n; j *= 2, m = k) 26 { 27 for(k = 0, i = n - j; i < n; ++i) y[k++] = i; 28 for(i = 0; i < n; ++i) if(sa[i] >= j) y[k++] = sa[i] - j; 29 for(i = 0; i < n; ++i) wv[i] = x[y[i]]; 30 for(i = 0; i < m; ++i) ws_[i] = 0; 31 for(i = 0; i < n; ++i) ws_[wv[i]]++; 32 for(i = 1; i < m; ++i) ws_[i] += ws_[i - 1]; 33 for(i = n - 1; i >= 0; --i) sa[--ws_[wv[i]]] = y[i]; 34 t = x; 35 x = y; 36 y = t; 37 for(x[sa[0]] = 0, i = k = 1; i < n; ++i) 38 x[sa[i]] = (y[sa[i - 1]] == y[sa[i]] && y[sa[i - 1] + j] == y[sa[i] + j]) ? k - 1 : k++; 39 } 40 } 41 int Rank[MAXN], height[MAXN], sa[MAXN], r[MAXN]; 42 void calheight(int *r,int *sa,int n) 43 { 44 int i,j,k=0; 45 for(i=1; i<=n; i++)Rank[sa[i]]=i; 46 for(i=0; i<n; height[Rank[i++]]=k) 47 for(k?k--:0,j=sa[Rank[i]-1]; r[i+k]==r[j+k]; k++); 48 } 49 int n,minnum[MAXN][17]; 50 void RMQ() 51 { 52 int i,j; 53 int m=(int)(log(n*1.0)/log(2.0)); 54 for(i=1;i<=n;i++) 55 minnum[i][0]=height[i]; 56 for(j=1;j<=m;j++) 57 for(i=1;i+(1<<j)-1<=n;i++) 58 minnum[i][j]=min(minnum[i][j-1],minnum[i+(1<<(j-1))][j-1]); 59 } 60 int Ask_MIN(int a,int b) 61 { 62 int k=int(log(b-a+1.0)/log(2.0)); 63 return min(minnum[a][k],minnum[b-(1<<k)+1][k]); 64 } 65 int calprefix(int a,int b) 66 { 67 a=Rank[a],b=Rank[b]; 68 if(a>b) 69 swap(a,b); 70 return Ask_MIN(a+1,b); 71 } 72 char s[MAXN]; 73 int q[MAXN]; 74 int main() 75 { 76 while (~scanf("%s",s)){ 77 int k = strlen(s); 78 s[k] = 'z'+1; 79 scanf("%s",s+k+1); 80 int n = strlen(s); 81 for (int i=0;i<n;i++){ 82 r[i] = s[i]-'a'+1; 83 } 84 int maxx = 0; 85 Suffix(r,sa,n+1,28); 86 calheight(r,sa,n); 87 for (int i=1;i<=n;i++){ 88 if (height[i]>maxx && 1ll*(sa[i]-k)*(sa[i-1]-k)<0) 89 maxx = height[i]; 90 } 91 printf("%d ",maxx); 92 } 93 return 0; 94 }