题目链接:https://ac.nowcoder.com/acm/contest/5668/E
题目大意:

想法:
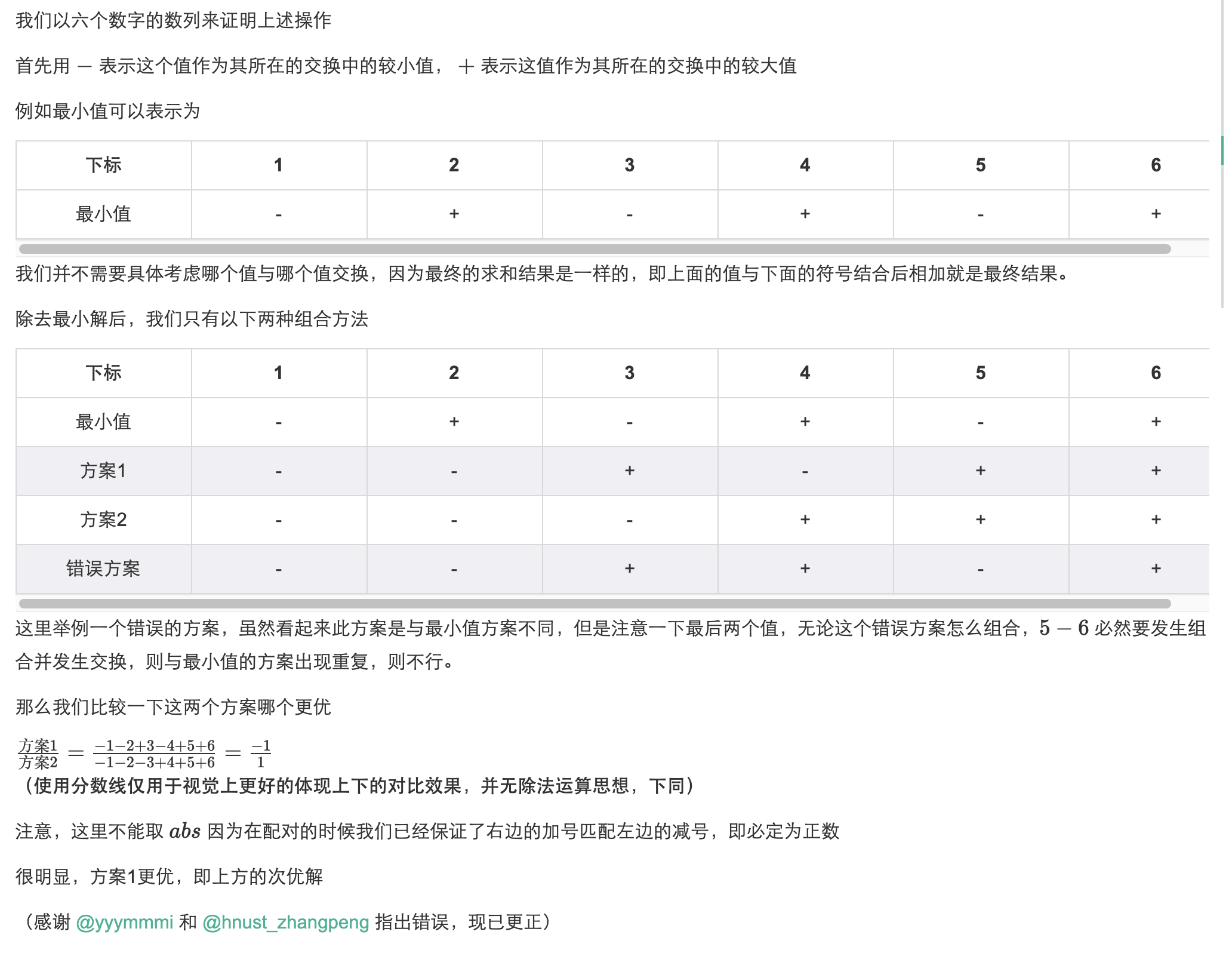
我们先考虑最小值:
我们假设排序后的下标的序列是:1、2、3、4、5、6
那么很简单我们得到的最小值就是 [(2 - 1) + (4 - 3) + (6 - 5)]
我们再来考虑次小值:
由于我们一句确定了最小值,所以对于次小值有很大的限制
以上的证明来自:https://blog.nowcoder.net/n/6facdc43054c4f098b42b2b584de217e?f=comment
我们将两个解相加得到答案:
(2 - 1) + (4 - 3) + (6 - 5) + (3 - 2) + (5 - 4) + (6 - 1) = 2 * (6 - 1)
1、当长度没有达到 6 的时候
对于长度为 4 的时候:
最终的结果很容易得到: 2 * (4 - 1)
2、长度为 8 的时候
我们可以考虑两个方案,转化成两个长度为 4 的 或者 直接一个长度为 8 的
长度为四的我们用类似证明里面的方法可以发现: (1234 和 5678 这种策略是最优秀的)
我们再用这种优秀的策略去和直接选择一个长度为 8 的对比,发现选择两个长度为 4 的是最优的
3、推广一下,当长度更长的时候
当长度 >= 10 的时候,我们可以考虑把这个串分成多个 长度为 4 和 长度为 6 的串
那么我们就可以得到 dp 的递推公式: dp[i] = min(dp[i - 4] + v[i - 1] - v[i - 4] , dp[i - 6] + v[i - 1] - v[i - 6])
我们对于 dp 进行初始化的时候必须要初始化 dp[4] dp[6] dp[8] 【防止 8 的时候被分成有长度为 2 的】
#include <algorithm> #include <string> #include <cstring> #include <vector> #include <map> #include <stack> #include <set> #include <queue> #include <cmath> #include <cstdio> #include <iomanip> #include <ctime> #include <bitset> #include <cmath> #include <sstream> #include <iostream> #include <unordered_map> #define ll long long #define ull unsigned long long #define ls nod<<1 #define rs (nod<<1)+1 #define pii pair<int,int> #define mp make_pair #define pb push_back #define INF 0x3f3f3f3f #define max(a, b) (a>b?a:b) #define min(a, b) (a<b?a:b) const double eps = 1e-8; const int maxn = 2e5 + 10; const ll MOD = 1e9 + 7; const int mlog=20; int sgn(double a) { return a < -eps ? -1 : a < eps ? 0 : 1; } using namespace std; ll f[maxn]; int main() { ios::sync_with_stdio(false); int t; cin >> t; while (t--) { int n; cin >> n; vector<ll> v; for (int i = 0;i < n;i++) { ll x; cin >> x; v.pb(x); } sort(v.begin(),v.end()); f[0] = 0; f[4] = v[3] - v[0]; f[6] = v[5] - v[0]; f[8] = v[7] - v[4] + f[4]; for (int i = 10;i <= n;i += 2) f[i] = min(f[i - 4] + v[i - 1] - v[i - 4],f[i - 6] + v[i - 1] - v[i - 6]); cout << f[n] * 2 << endl; } return 0; }