题目分析
-
给定一张n*n的芯片。
'.'表示该格子可以放一个零件。
'C'表示该格子已经放了一个零件(不能拆下)。
'/'表示该格子不能放零件。
要求在芯片的现有基础上,放置尽可能多的零件,使得:
- 第i行与第i列零件数相等。
- 每行每列零件数<=总零件数*A/B。
条件1
-
考虑如何使得第i行第j列零件数相等。
首先可以想到经典的行列二分图模型,即((i,j))如果可放置零件,则连边;如果必须放置零件,则记录其为必选。最后跑最大流即可。
然而这种模型的局限性就在于无法控制行列相等。
-
我们考虑用逆向思维解决:((i,j))如果可放置零件,则连边;如果必须放置零件,则不连。而边的意义为点((i,j))不放零件。
这样有什么好处呢?
既然原始边为不放零件,那我们就可以在((i,i))之间连接新边,来收集剩余流量。
如何理解?
设第i行可放置和必须放置零件总和为(a[i]),而已经流出(x)流量表示不选,第i列同理。则我们可以用新边收集((i,i))之间剩余的流量,而这里的流量就表示选择放置零件。
样例分析(不考虑条件2):
n=2 C. /.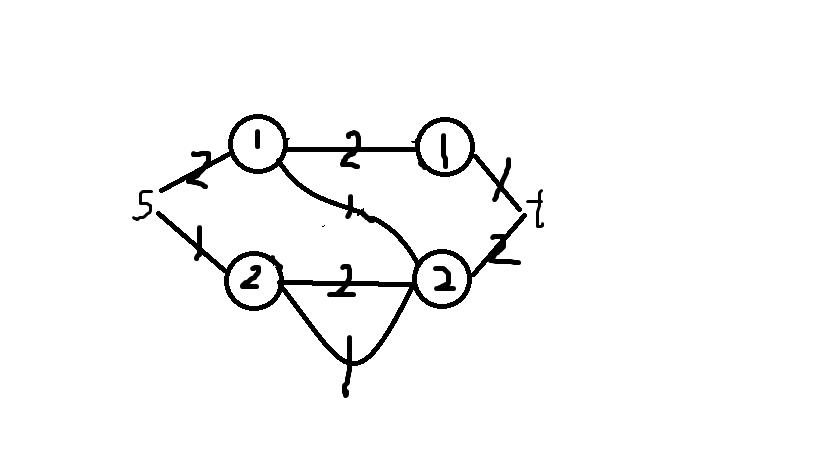
如图,行列间的曲线为表示不选的原始边,直线为表示选择的新边。
同时由于(1,1)为'C',我们记录下它的流量并体现在选择边中,但不建立表示不选的曲线。
则选择的最大流量为2,不选的边(1,2)流量为1,即最大流=3。
最终答案为选择的最大流量2-已有的必选流量1=1。
-
分析上面样例的求解过程,我们不难发现需要跑最大流,检查最大流是否等于所有可选与必选的流量和来判断是否有解(想一想为什么)。
然而问题在于如何控制流量尽可能经过收集流量的直线边?
可见是要在所有最大流中,选择收集流量最多的那一种,考虑用添加费用作为优先级的方式来实现。
我们使得所有选择边的优先级为1,所有不选边的优先级为0,而优先级体现在网络流中就是费用。
这样跑最大费用最大流即可,求出的最大流=选与不选的流量总和,最大费用=选的流量总和,答案=最大费用-已有的必选流量。
条件2
-
解决了行列相等的问题,但题目还要求每条选择边的流量<=总费用*A/B。
也就是说,我们需要对新建的选择边容量进行限流,使其<=总费用*A/B。
然而总费用需要建边后求出,而建边需要总费用进行限流。(明显该算法被条件2锁死)
因此我们不能被动地去等待总费用被求出,而应该主动枚举。
-
考虑枚举总费用,这样就能求出选择边的容量限制,完成建图。
跑完最大费用最大流,检查我们求出的费用是否等于所枚举的总费用值,等于则更新答案。
题目n<=40,枚举总费用复杂度(n^2),费用流复杂度怎么也得比最大流的(sqrt n m)要大,也就是说(n^4)乃至(n^5)的复杂度在这道题是非常危险的。
-
考虑一种常见的优化方式:保持上次枚举费用所跑出的残留网络不动,更改选择边的容量限制,然后继续跑费用流。
然而这种方式在这道题是行不通的,假设这次选择边的容量限制+=1,那么在继续跑费用流之前,这张图的当前流可能已经不是最大费用流了(想一想为什么)。而我们的spfa+dinic实质上是一种贪心,是必须保证当前流时刻是最大费用流的!
可能还可以加个消圈算法来调整,但是编程难度较大,我们考虑直接改变枚举思路。
-
当容量限制lim确定时,我们所跑出来的总费用也必然确定。
因此,完全没有必要枚举总费用,我们只要枚举容量限制lim,然后检查总费用是否满足条件2即可。
也就是说,(n)复杂度枚举容量限制lim,然后求出最大总费用maxw,只要(lim<=maxw*A/B)便能够满足条件2,更新答案即可。
最终答案取所有可能解中的最大值。
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
#define fakemain main
#define inf 0x3f3f3f3f
using namespace std;
const int MAXN=110;
int n,s,t,A,B;
char ss[MAXN][MAXN];
int a[MAXN];//统计每行每列的总流量
int b[MAXN];//记录每行每列的已有流量
int en=-1,eh[MAXN];
struct edge
{
int v,c,w,next;
edge(int V=0,int C=0,int W=0,int N=0):v(V),c(C),w(W),next(N){}
};edge e[MAXN*MAXN];
inline void add_edge(int u,int v,int c,int w)
{
e[++en]=edge(v,c,w,eh[u]);eh[u]=en;
e[++en]=edge(u,0,-w,eh[v]);eh[v]=en;
}
void input()
{
s=n*2+1;t=n*2+2;
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
for(int i=1;i<=n;++i)
{
scanf("%s",ss[i]+1);
for(int j=1;j<=n;++j)
{
if(ss[i][j]=='C' || ss[i][j]=='.'){++a[i];++a[j+n];}
if(ss[i][j]=='C'){++b[i];++b[j+n];}
}
}
en=-1;
memset(eh,-1,sizeof(eh));
for(int i=1;i<=n;++i)add_edge(i,i+n,0,-1);//添加可选取边,初始容量为0
for(int i=1;i<=n;++i)
for(int j=1;j<=n;++j)if(ss[i][j]=='.')//添加不选边
add_edge(i,j+n,1,0);
for(int i=1;i<=n;++i)//添加源汇边
{
add_edge(s,i,a[i],0);
add_edge(i+n,t,a[i+n],0);
}
}
int tota,totb,rstf,lim;//总流量总和,已使用流量总和,源点流量,可选取边容量限制
int maxw,ans;
void init()//容量初始化
{
for(int i=1;i<=n;++i){e[i*2-2].c=lim;e[i*2-1].c=0;}
for(int i=n+1;i<=(en+1)/2;++i)
{
e[i*2-2].c+=e[i*2-1].c;
e[i*2-1].c=0;
}
}
int dis[MAXN],cur[MAXN];
bool inq[MAXN];
bool vis[MAXN];
deque<int> q;
bool spfa()
{
fill(dis+1,dis+t+1,inf);
dis[s]=0;q.push_back(s);inq[s]=1;
int u,v,w;
while(!q.empty())
{
u=q.front();q.pop_front();inq[u]=0;
for(int i=eh[u];i!=-1;i=e[i].next)if(e[i].c)
{
v=e[i].v;w=e[i].w;
if(dis[v]>dis[u]+w)
{
dis[v]=dis[u]+w;
if(!inq[v])
{
inq[v]=1;
if(!q.empty() && dis[v]<dis[q.front()])q.push_front(v);
else q.push_back(v);
}
}
}
}
return dis[t]!=inf;
}
int dfs(int u,int flow)
{
if(u==t)
{
maxw+=-dis[t]*flow;
return flow;
}
vis[u]=1;
int v,f,used=0;
for(int i=cur[u];i!=-1;i=e[i].next)if(e[i].c)
{
cur[u]=i;
v=e[i].v;
if(dis[u]+e[i].w==dis[v] && !vis[v])
{
f=dfs(v,min(flow-used,e[i].c));
e[i].c-=f;
e[i^1].c+=f;
used+=f;
if(used==flow)break;
}
}
vis[u]=0;
return used;
}
void solve()
{
ans=-inf;tota=0;totb=0;
for(int i=1;i<=n;++i){tota+=a[i];totb+=b[i];}
for(lim=0;lim<=n;++lim)//枚举可选取边的限制lim
{
init();
rstf=tota;maxw=0;
while(rstf && spfa())//存在未使用流量,且存在増广路
{
memcpy(cur,eh,sizeof(cur));
rstf-=dfs(s,rstf);
}
//如果用尽,且lim符合散热,则为可行解,更新答案
if(!rstf && lim<=maxw*A/B)ans=max(ans,maxw-totb);
}
}
void output()
{
if(ans==-inf)printf("impossible
");
else printf("%d
",ans);
}
int fakemain()
{
// freopen("in.txt","r",stdin);
int cnt=0;
while(1)
{
scanf("%d %d %d",&n,&A,&B);
if(n==0)return 0;
printf("Case %d: ",++cnt);
input();
solve();
output();
}
}