「JLOI2015」「LOJ #2107」城池攻占

Description

Hint

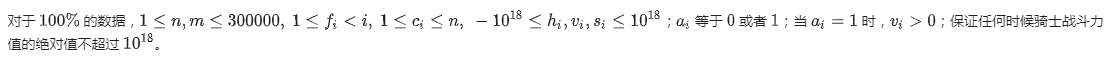
Solution

首先可以知道，树的每一个结点都要维护一个数集，表示该结点出发的骑士。

我们从叶结点开始做，每到一个结点，先“砍掉”一部分权值过小的骑士，然后再将这个城池的数集与其父城池 合并。

对于这个数集，我们可以选择合适的数据结构维护。

平衡树？貌似可以但是合并只能启发式合并，因此时间复杂度中会有两个 (log)……

线段树？虽然时间复杂度降到了 (O(nlog n))，但是非常炸空间……

有没有又快又省空间的方法？可并堆（左偏树）！

---

如何对左偏树中的元素进行修改？打标记！

我们仿照线段树的标记下传的方式，在每次合并中，以及弹出树根前 pushdown 一遍。

标记更新的顺序显然是先乘后加。

---

复杂度分析：

由于左偏树的每个结点（骑士）只会插入或弹出一次，于是这里的复杂度为 (O(mlog n))。

在这个 (n) 个结点的树上会有 (n) 次合并，于是这里复杂度为 (O(nlog n))。

总时间复杂度显然是 (O(nlog n))，空间只需 (O(n))。

Code

/*
 * Author : _Wallace_
 * Source : https://www.cnblogs.com/-Wallace-/
 * Problem : LOJ #2107 JLOI2015 城池攻占
 */
#include <algorithm>
#include <iostream>

using namespace std;
const int N = 3e5 + 5;

#define lc t[x].ch[0]
#define rc t[x].ch[1]
struct ltNode {
	int ch[2], rt;
	int dist;
	long long val;
	long long add, mul;
	ltNode() : mul(1) { }
} t[N];
int n, m;

inline void setAdd(int x, long long v) {
	t[x].add += v, t[x].val += v;
}
inline void setMul(int x, long long v) {
	t[x].mul *= v, t[x].add *= v, t[x].val *= v;
}
inline void pushdown(int x) {
	if (lc) setMul(lc, t[x].mul), setAdd(lc, t[x].add);
	if (rc) setMul(rc, t[x].mul), setAdd(rc, t[x].add);
	t[x].add = 0, t[x].mul = 1;
}

int merge(int x, int y) {
	if (!x || !y) return x | y;
	pushdown(x), pushdown(y);
	if (t[x].val > t[y].val) swap(x, y);
	rc = merge(rc, y);
	if (t[lc].dist < t[rc].dist) swap(lc, rc);
	t[lc].rt = t[rc].rt = t[x].rt = x;
	t[x].dist = t[rc].dist + 1;
	return x;
}
int findrt(int x) {
	return x == t[x].rt ? x : t[x].rt = findrt(t[x].rt);
}

struct city {
	int fa, type;
	long long def, val;
	int root, depth, ans;
} ct[N];
struct knight {
	int start;
	long long val;
	int last;
} kt[N];

signed main() {
	ios::sync_with_stdio(false);
	cin >> n >> m;
	for (register int i = 1; i <= n; i++)
		cin >> ct[i].def;
	for (register int i = 2; i <= n; i++)
		cin >> ct[i].fa >> ct[i].type >> ct[i].val;
	for (register int i = 1; i <= m; i++)
		cin >> kt[i].val >> kt[i].start;
	
	t[0].dist = -1;
	for (register int i = 1; i <= m; i++)
		t[i].val = kt[i].val, t[i].rt = i;
	for (register int i = 1; i <= m; i++)
		ct[kt[i].start].root = merge(ct[kt[i].start].root, i);
	ct[1].depth = 1;
	for (register int i = 2; i <= n; i++)
		ct[i].depth = ct[ct[i].fa].depth + 1;
	for (register int i = n; i; i--) {
		while (ct[i].root && t[ct[i].root].val < ct[i].def) {
			pushdown(ct[i].root);
			kt[ct[i].root].last = i;
			++ct[i].ans;
			ct[i].root = merge(t[ct[i].root].ch[0], t[ct[i].root].ch[1]);
		}
		if (ct[i].type) setMul(ct[i].root, ct[i].val);
		else setAdd(ct[i].root, ct[i].val);
		ct[ct[i].fa].root = merge(ct[ct[i].fa].root, ct[i].root);
	}
	
	for (register int i = 1; i <= n; i++)
		cout << ct[i].ans << endl;
	for (register int i = 1; i <= m; i++)
		cout << ct[kt[i].start].depth - ct[kt[i].last].depth << endl;
	return 0;
}