第5章 树
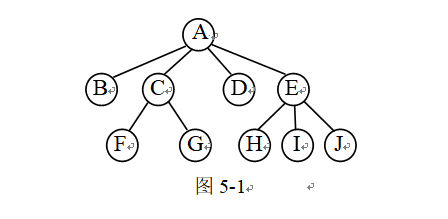
【例5-1】写出如图5-1所示的树的叶子结点、非终端结点、每个结点的度及树深度。
|
解:
(1)叶子结点有:B、D、F、G、H、I、J。
(2)非终端结点有:A、C、E。
(3)每个结点的度分别是:A的度为4,C的度为2,E的度为3,其余结点的度为0。
(4)树的深度为3。
【例5-2】一棵度为2的树与一棵二叉树有什么区别?
解:度为2的树有两个分支,但分支没有左右之分;一棵二叉树也有两个分支,但有左右之分,左右子树的次序不能交换。
【例5-3】树与二叉树有什么区别?
解:区别有两点:
(1)二叉树的一个结点至多有两个子树,树则不然;
(2)二叉树的一个结点的子树有左右之分,而树的子树没有次序。
//二叉树有顺序,最多度为二
【例5-4】分别画出具有3个结点的树和三个结点的二叉树的所有不同形态。
解:如图5-2(a)所示,具有3个结点的树有两种不同形态。

|
|
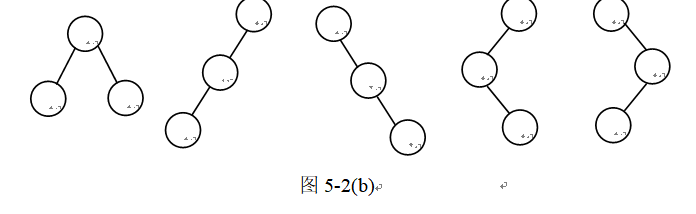
如图5-2(b)所示,具有3个结点的二叉树有以下五种不同形态。
|
|
【例5-5】在一棵度为m树中,度为1的结点数为n1,度为2的结点数为n2,……,度为m的结点数为nm,则该数中含有多少个叶子结点?有多少个非终端结点?
解:设度为0的结点(即叶子结点)数目为n0,树中的分支数为B,树中总的结点数为N,则有:
(1)从结点的度考虑:
N= n0+ n1+ n2+……+nm
(2)从分支数目考虑:一棵树中只有一个根结点,其他的均为孩子结点,而孩子结点可以由分支数得到。所以有:
N=B+1=0×n0+1×n1+2×n2+…+m×nm+1。。。。
由以上两式,可得
n0+ n1+ n2+……+nm=0×n0+1×n1+2×n2+…+m×nm+1
从而可导出叶子结点的数目为:
n0=0×n1+1×n2+…+(m-1)×nm+1=1+。。。。。。
从而可以得到非终端结点的数目为
N- n0= n1+ n2+……+nm=。。。。。。。
【例5-6】一棵含有n个结点的k叉树,可能达到的最大深度和最小深度各为多少?
解:(1)当k叉树中只有一层的分支数为k,其它层的分支数均为1时,此时的树具有最大的高度,为:n-k+1。//n-k是分支为1,1是分支为k
(2)当该k叉树为完全k叉树时,其深度最小。参照二叉树的性质4可知,其深度为:
+1。
【例5-7】证明任何一棵满二叉树T中的分支数B满足B=2(n0-1)(其中n0为叶子结点数)。
证明:
∵T为满二叉树
∴不存在度为1的结点
设该二叉树中总的结点数为n,度为2的结点总数为n2,分支数为B
则有n=n0+ n2 ①
又∵除了根结点外,其余n-1个结点都有一个分支进入,即有n个结点的二叉树共有n-1条边
∴n=B+1 ②
由①、②两式,可得 B+1=n0+ n2 ③
又由二叉树的性质3可知 n2=n0-1 ④
由③、④两式可知 B= n0+ n0-1-1=2(n0-1) 求证成立。
//这题真的很想卧槽啊
【例5-8】如图5-3所示的二叉树,试分别写出它的顺序表示和链接表示(二叉链表)。
//二叉树的顺序表示和链式表示
解:
(1)顺序表示。
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
a |
b |
c |
d |
e |
^ |
^ |
^ |
^ |
f |
g |
(2)该二叉树的二叉链表表示如图5-4所示。

【例5-9】试找出满足下列条件的所有二叉树:
(1)先序序列和中序序列相同;
(2)中序序列和后序序列相同;
(3)先序序列和后序序列相同。
解:
(1)先序序列和中序序列相同的二叉树为:空树或者任一结点均无左孩子的非空二叉树;(右单支树)
(2)中序序列和后序序列相同的二叉树为:空树或者任一结点均无右孩子的非空二叉树;(左单支树)
(3)先序序列和后序序列相同的二叉树为:空树或仅有一个结点的二叉树。
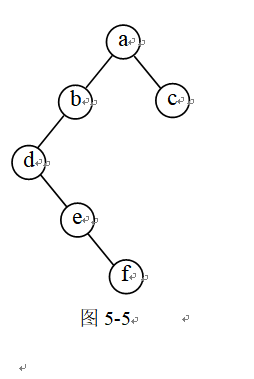
【例5-10】如图5-5所示的二叉树,要求:
(1)写出按先序、中序、后序遍历得到的结点序列。
(2)画出该二叉树的后序线索二叉树。
解:
(1) 先序遍历序列:ABDEFC
中序遍历序列:DEFBAC
后序遍历序列:FEDBCA
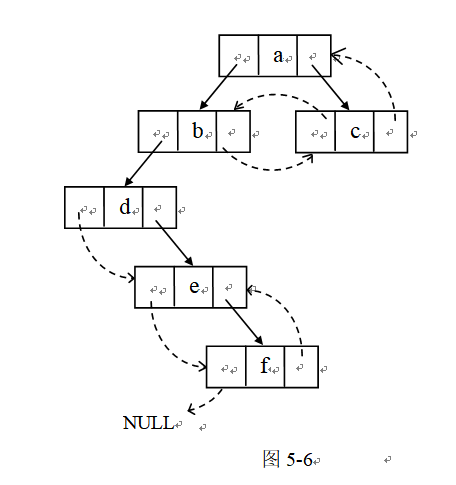
(2)其后序线索二叉树如图5-6所示。//暂时只考中序线索二叉树
|
|
【例5-11】将图5-7所示的树转换为二叉树。
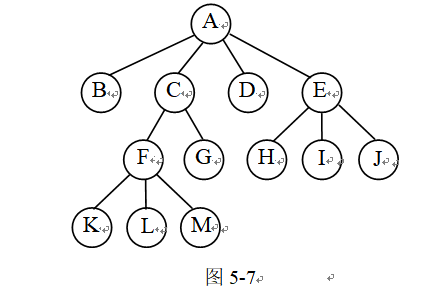
解:第一步,加线。第二步,抹线。第三步,旋转。过程如图5-8所示。
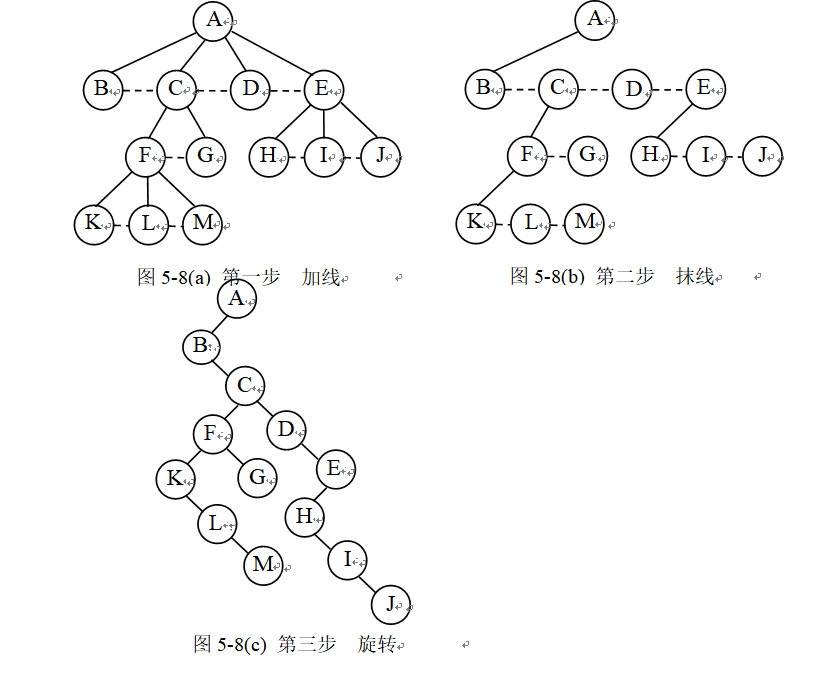
|
|
【例5-12】将如图5-9所示的二叉树转换为树。
解: 第一步,加线。第二步,抹线。第三步,调整。过程如图5-10所示。

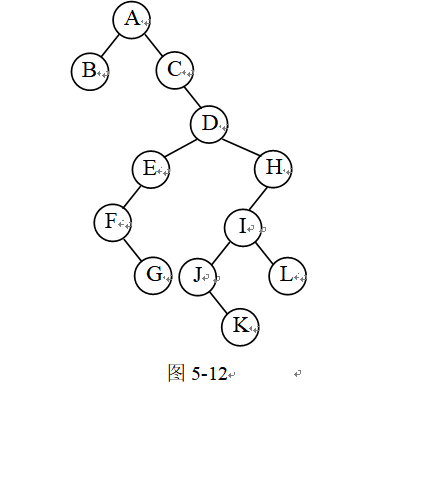
【例5-13】将如图5-11所示的森林转换成二叉树。//左孩子右兄弟

解: 步骤略,结果如图5-12所示。
【例5-14】假定用于通信的电文由8个字符A、B、C、D、E、F、G、H组成,各字母在电文中出现的概率为5%、25%、4%、7%、9%、12%、30%、8%,试为这8个字母设计哈夫曼编码。
解: 根据题意,设这8个字母对应的权值分别为(5,25,4,7,9,12,30,8),并且n=8。
(1)设计哈夫曼树的步骤如图5-13所示。//它一直保持第一层是要排序的数所以不会乱

(2)设计哈夫曼编码
利用第八步得到的哈夫曼树,规定左分支用0表示,右分支用1表示,字母A、B、C、D、E、F、G、H的哈夫曼编码如下表示:
A:0011 B:01 C:0010 D:1010
E:000 F:100 G:11 H:1011
习题5
一、单项选择题
1. 在一棵度为3的树中,度为3的结点数为2个,度为2的结点数为1个,度为1的结点数为2个,则度为0的结点数为( C)个。//1+2+3=6
A. 4 B. 5 C. 6 D. 7
2. 假设在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为(B )个。//n0=n2+1
A. 15 B. 16 C. 17 D. 47
3. 假定一棵三叉树的结点数为50,则它的最小高度为(C )。//公式算不出来就画一画
A. 3 B. 4 C. 5 D. 6
4. 在一棵二叉树上第4层的结点数最多为( D)。
A. 2 B. 4 C. 6 D. 8
5. 用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组中R[1..n],结点R[i]若有左孩子,其左孩子的编号为结点(B)。//左孩子2i右孩子2i+1;若2i/2i+1>n,无左右孩子
A. R[2i+1] B. R[2i] C. R[i/2] D. R[2i-1]
6. 由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为(D )。
A. 24 B. 48 C. 72 D. 53
//在这个树构造这种题上,你已经因为同一原因出错好几次了。原因:两个数字加和之后,要代替两个数字放回原来数列中重新选择。
7. 线索二叉树是一种( C)结构。
A. 逻辑 B. 逻辑和存储 C. 物理 D. 线性
8. 线索二叉树中,结点p没有左子树的充要条件是( B)。
A. p->lc=NULL B. p->ltag=1
C. p->ltag=1 且p->lc=NULL D. 以上都不对
9. 设n , m 为一棵二叉树上的两个结点,在中序遍历序列中n在m前的条件是(B)。
A. n在m右方 B. n在m 左方
C. n是m的祖先 D. n是m的子孙
10. 如果F是由有序树T转换而来的二叉树,那么T中结点的前序就是F中结点的(B )。
A. 中序 B. 前序 C. 后序 D. 层次序//记住前序对应前序
11. 欲实现任意二叉树的后序遍历的非递归算法而不必使用栈,最佳方案是二叉树采用( A)存储结构。
A. 三叉链表 B. 广义表 C. 二叉链表 D. 顺序
12. 下面叙述正确的是(D)。
A. 二叉树是特殊的树 //二叉树不是特殊的树
B. 二叉树等价于度为2的树
C. 完全二叉树必为满二叉树
D. 二叉树的左右子树有次序之分
13. 任何一棵二叉树的叶子结点在先序、中序和后序遍历序列中的相对次序(A )。
A. 不发生改变 B. 发生改变
C. 不能确定 D. 以上都不对
14. 已知一棵完全二叉树的结点总数为9个,则最后一层的结点数为(B )。
A. 1 B. 2 C. 3 D. 4
15. 根据先序序列ABDC和中序序列DBAC确定对应的二叉树,该二叉树( A )。
A. 是完全二叉树 B. 不是完全二叉树
C. 是满二叉树 D. 不是满二叉树
二、判断题
1. 二叉树中每个结点的度不能超过2,所以二叉树是一种特殊的树。 (× )
2. 二叉树的前序遍历中,任意结点均处在其子女结点之前。 (√ )
3. 线索二叉树是一种逻辑结构。 //存储结构 (×)
4. 哈夫曼树的总结点个数(多于1时)不能为偶数。 (√)
5. 由二叉树的先序序列和后序序列可以唯一确定一颗二叉树。 (×)
6. 树的后序遍历与其对应的二叉树的后序遍历序列相同。//正常情况是对应的(√)
7. 根据任意一种遍历序列即可唯一确定对应的二叉树。 (√)
8. 满二叉树也是完全二叉树。 (√)
9. 哈夫曼树一定是完全二叉树。 (×)
10. 树的子树是无序的。//二叉树的子树有序 (×)
三、填空题
1. 假定一棵树的广义表表示为A(B(E),C(F(H,I,J),G),D),则该树的度为_3____,树的深度为__4___,终端结点的个数为____6__,单分支结点的个数为__1____,双分支结点的个数为____1__,三分支结点的个数为____2___,C结点的双亲结点为___A____,其孩子结点为____F___和___G____结点。1. 3,4,6,1,1,2,A,F,G
2. 设F是一个森林,B是由F转换得到的二叉树,F中有n个非终端结点,则B中右指针域为空的结点有____ n+1___个。//画一画
3. 对于一个有n个结点的二叉树,当它为一棵____完全____二叉树时具有最小高度,即为_______,当它为一棵单支树具有____最大___高度,即为__ n _____。
4. 由带权为3,9,6,2,5的5个叶子结点构成一棵哈夫曼树,则带权路径长度为__ 55_。
5. 在一棵二叉排序树上按____中序___遍历得到的结点序列是一个有序序列。
6. 对于一棵具有n个结点的二叉树,当进行链接存储时,其二叉链表中的指针域的总数为2n _______个,其中_____ n-1__个用于链接孩子结点,___ n+1____个空闲着。
7. 在一棵二叉树中,度为0的结点个数为n0,度为2的结点个数为n2,则n0=__ n2+1____。
8. 一棵深度为k的满二叉树的结点总数为____2k-1___,一棵深度为k的完全二叉树的结点总数的最小值为___2k-1__,最大值为__2k-1____。
9. 由三个结点构成的二叉树,共有__5__种不同的形态。
10. 设高度为h的二叉树中只有度为0和度为2的结点,则此类二叉树中所包含的结点数至少为__ 2h-1__。//就是完全二叉树啊
11. 一棵含有n个结点的k叉树,___单支树___形态达到最大深度,___完全二叉树_形态达到最小深度。
12. 对于一棵具有n个结点的二叉树,若一个结点的编号为i(1≤i≤n),则它的左孩子结点的编号为____2i ____,右孩子结点的编号为____2i+1____,双亲结点的编号为__ëi/2û______。
13. 对于一棵具有n个结点的二叉树,采用二叉链表存储时,链表中指针域的总数为_____ 2n ____个,其中________ n-1___个用于链接孩子结点,__________ n+1___个空闲着。
14. 哈夫曼树是指____________带权路径长度最小_______________的二叉树。
15. 空树是指______结点数为0__________________,最小的树是指_______________只有一个根结点的树________。
16. 二叉树的链式存储结构有_______二叉链表_______和_________三叉链表______两种。
17. 三叉链表比二叉链表多一个指向_________双亲结点_____的指针域。
18. 线索是指_______________指向结点前驱和后继信息的指针__________。
19. 线索链表中的rtag域值为__1___时,表示该结点无右孩子,此时__Rchild____域为指向该结点后继线索的指针。
20. 本节中我们学习的树的存储结构有__孩子表示法_______、____双亲表示法_______和_______长子兄弟表示法____。
四、应用题
1. 已知一棵树边的集合为{<i,m>,<i,n>,<e,i>,<b,e>,<b,d>,<a,b>,<g,j>,<g,k>,<c,g>,<c,f>,<h,l>,<c,h>,<a,c>},请画出这棵树,并回答下列问题:
(1)哪个是根结点?
(2)哪些是叶子结点?
(3)哪个是结点g的双亲?
(4)哪些是结点g的祖先?
(5)哪些是结点g的孩子?
(6)哪些是结点e的孩子?
(7)哪些是结点e的兄弟?哪些是结点f的兄弟?
(8)结点b和n的层次号分别是什么?
(9)树的深度是多少?
(10)以结点c为根的子树深度是多少?
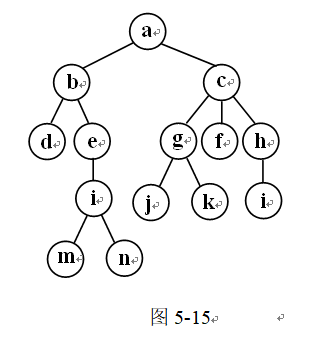
1. 解答:
根据给定的边确定的树如图5-15所示。
其中根结点为a;
叶子结点有:d、m、n、j、k、f、l;
c是结点g的双亲;
a、c是结点g的祖先;
j、k是结点g的孩子;
m、n是结点e的子孙;
e是结点d的兄弟;
g、h是结点f的兄弟;
结点b和n的层次号分别是2和5;
树的深度为5。
2. 一棵度为2的树与一棵二叉树有何区别。
2. 解答:
度为2的树有两个分支,但分支没有左右之分;一棵二叉树也有两个分支,但有左右之分,左右子树不能交换。//二叉树有次序
3. 试分别画出具有3个结点的树和二叉树的所有不同形态?
3. 解答: 3个结点的树有两种形态,3个结点的二叉树有5种形态
4. 已知用一维数组存放的一棵完全二叉树:ABCDEFGHIJKL,写出该二叉树的先序、中序和后序遍历序列。
4. 解答:
先序序列:ABDHIEJKCFLG
中序序列:HDIBJEKALFCG
后序序列:HIDJKEBLFGCA
5. 一棵深度为H的满k叉树有如下性质:第H层上的结点都是叶子结点,其余各层上每个结点都有k棵非空子树,如果按层次自上至下,从左到右顺序从1开始对全部结点编号,回答下列问题:
(1)各层的结点数目是多少?
(2)编号为n的结点的父结点如果存在,编号是多少?
(3)编号为n的结点的第i个孩子结点如果存在,编号是多少?
(4)编号为n的结点有右兄弟的条件是什么?其右兄弟的编号是多少?
5. 解答:
(1)第i层上的结点数目是mi-1。
(2)编号为n的结点的父结点如果存在,编号是((n-2)/m)+1。
(3)编号为n的结点的第i个孩子结点如果存在,编号是(n-1)*m+i+1。
(4)编号为n的结点有右兄弟的条件是(n-1)%m≠0。其右兄弟的编号是n+1。//心好累,这个题就先放过了
6. 找出所有满足下列条件的二叉树:
(1)它们在先序遍历和中序遍历时,得到的遍历序列相同;
(2)它们在后序遍历和中序遍历时,得到的遍历序列相同;
(3)它们在先序遍历和后序遍历时,得到的遍历序列相同;
6. 解答:
(1)先序序列和中序序列相同的二叉树为:空树或者任一结点均无左孩子的非空二叉树;
(2)中序序列和后序序列相同的二叉树为:空树或者任一结点均无右孩子的非空二叉树;
(3)先序序列和后序序列相同的二叉树为:空树或仅有一个结点的二叉树。
7. 假设一棵二叉树的先序序列为EBADCFHGIKJ,中序序列为ABCDEFGHIJK,请写出该二叉树的后序遍历序列。
7. 解答:后序序列:ACDBGJKIHFE
8. 假设一棵二叉树的后序序列为DCEGBFHKJIA,中序序列为DCBGEAHFIJK,请写出该二叉树的后序遍历序列。
8. 解答:先序序列:ABCDGEIHFJK
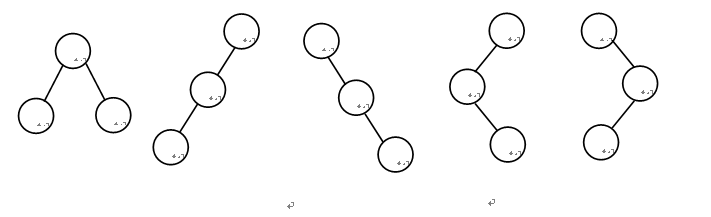
9. 给出如图5-14所示的森林的先根、后根遍历结点序列,然后画出该森林对应的二叉树。
9. 解答:
先根遍历:ABCDEFGHIJKLMNO //不用空格,一棵树遍历完了之后再遍历另一颗
后根遍历:BDEFCAHJIGKNOML
森林转换成二叉树如图5-16所示。
10.给定一组权值(5,9,11,2,7,16),试设计相应的哈夫曼树。
10. 解答:构造而成的哈夫曼树如图5-17所示。
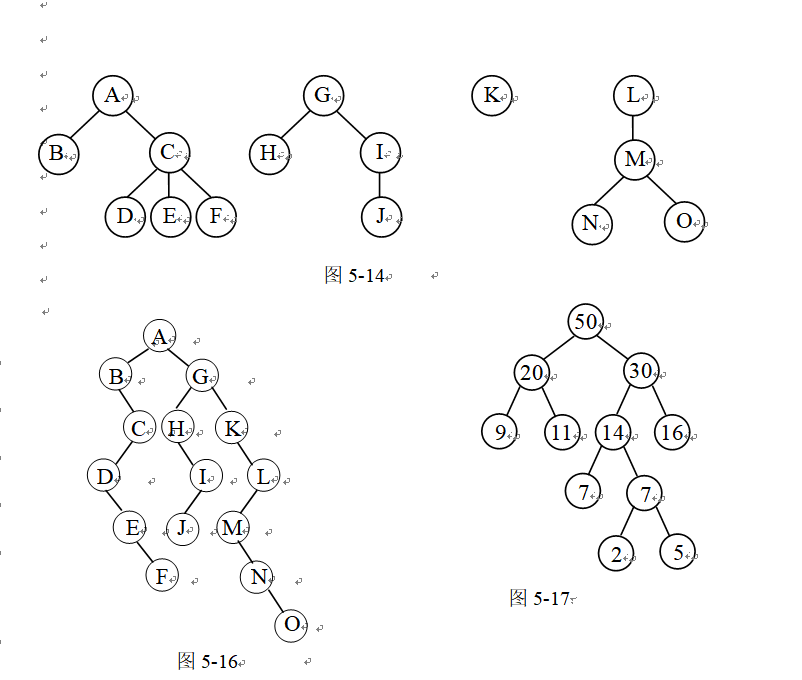
//终于写对哈夫曼树,心塞塞,小姑娘的少女心啊
五、算法设计题
1. 一棵具有n个结点的完全二叉树以一维数组作为存储结构,试设计一个对该完全二叉树进行先序遍历的算法。
1. 解答:这个问题可以用递归算法,也可用非递归算法,下面给出的为非递归算法。假设该完全二叉树的结点以层次为序,按照从上到下,同层从左到右顺序编号,存放在一个一维数组R[1..n]中,且用一个有足够大容量为maxlen的顺序栈作辅助存储,算法描述如下:
preorder (R) //先序遍历二叉树R
int R[n];
{ int root;
SqStack *s; //s为一个指针栈,类型为seqstack,其中包含top域和数组data
s->top= -1; //s栈置空
root=1;
while ((root<=n) && (s->top>-1))
{ while (root<=n)
{ printf(R[root]);
s->top++;
s->data[s->top]=root;
root=2*root;
}
if (s->top>-1) //栈非空访问,遍历右子树
{ root=s->data[s->top]*2+1;
s->top--;
}
}
}
2. 给定一棵用二叉链表表示的二叉树,其中的指针t指向根结点,试写出从根开始,按层次遍历二叉树的算法,同层的结点按从左至右的次序访问。
2. 解答:考虑用一个顺序队que来保存遍历过程中的各个结点,由于二叉树以二叉链表存储,所以可设que为一个指向数据类型为bitree的指针数组,最大容量为maxnum,下标从1开始,同层结点从左到右存放。算法中的front为队头指针,rear为队尾指针。
levelorder (BiTree *t) //按层次遍历二叉树t
{ BiTree *que[maxnum];
int rear,front;
if (t!=NULL)
{ front=0; //置空队列
rear=1;
que[1]=t;
do
{ front=front%maxsize+1; //出队
t=que[front];
printf(t->data);
if (t->lchild!=NULL) //左子树的根结点入队
{ rear=rear%maxsize+1;
que[rear]=t->lchild;
}
if (t->rchild!=NULL) //右子树的根结点入队
{ rear=rear%maxsize+1;
que[rear]=t->rchild;
}
}while (rear= =front); //队列为空时结束
}
}
3. 写出在中序线索二叉树中结点P的右子树中插入一个结点s的算法。
3. 解答:设该线索二叉树类型为bithptr,包含5个域:lchild,ltag,data,rchild,rtag。
insert(p, s) //将s结点作为p的右子树插入
BiThrNode *p,*s;
{ BiThrNode *q;
if (p->rtag= =1) //无右子树,则有右线索
{ s->rchild=p->rchild;
s->rtag=1;
p->rchild=s;
p->rtag=0;
}
else
{ q=p->rchild;
while(q->ltag= =0) //查找p所指结点中序后继,即为其右子树中最左下的结点
q=q->lchild;
q->lchild=p->rchild;
s->rtag=0;
p->rchild=s;
}
s->lchild=p; //将s结点的左线索指向p结点
s->ltag=1;
}
4. 给定一棵二叉树,用二叉链表表示,其根指针为t,试写出求该二叉树中结点n的双亲结点的算法。若没有结点n或者该结点没有双亲结点,分别输出相应的信息;若结点n有双亲,输出其双亲的值。
4. 解答:利用一个队列来完成,设该队列类型为指针类型,最大容量为maxnum。算法中的front为队头指针,rear为队尾指针,若当前队头结点的左、右子树的根结点不是所求结点,则将两子树的根结点入队,否则,队头指针所指结点即为结点的双亲。
parentjudge(t,n)
BiTree *t;
int n;
{ BiTree *que[maxnum];
int front,rear;
BiTree *parent;
parent=NULL;
if (t)
if (t->data= =n)
printf(“no parent!”); //n是根结点,无双亲
else
{ front=0; //初始化队列
rear=1;
que[1]=t; //根结点进队
do
{ front=front%maxsize+1;
t=que[front];
if((t->lchild->data= =n)|| (t->rchild->data= =n)) //结点n有双亲
{ parent=t;
front=rear;
printf(“parent”,t->data);
}
else
{ if (t->lchild!=NULL) //左子树的根结点入队
{ rear=rear%maxsize+1;
que[rear]=t->lchild;
}
if (t->rchild!=NULL) //右子树的根结点入队
{ rear=rear%maxsize+1;
que[rear]=t->rchild;
}
}
}while(rear= =front); //队空时结束
if (parent = =NULL)
printf(“结点不存在”);
}
}