2020牛客暑期多校训练营（第五场）解题报告

F

---

温柔的签到题。

注意这里使用c++的ceil函数会有误差，需要自己手动ceil。注意手动ceil的时候可能会爆long long。

#include <bits/stdc++.h>
 
using namespace std;
 
#define ll long long
ll input(){
    ll x=0,f=0;char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return f? -x:x;
}
 
const int N=107;
 
ll a[N];
ll mx=0;
 
ll cal(ll a){
    ll fz=a*50,fm=mx;
    ll ans=fz/fm;
    if(fz%fm!=0) ans++;
    return ans;
}
 
int main(){
    int n=input();
 
    for(int i=1;i<=n;i++){
        a[i]=input();
        mx=max(a[i],mx);
    }
 
    for(int i=1;i<=n;i++){
        int len=cal(a[i]);
 
        printf("+");
        for(ll i=1;i<=len;i++) printf("-");
        printf("+
");
 
        printf("|");
        for(ll i=1;i<len;i++)printf(" ");
        if(len!=0){
            if(mx==a[i]) printf("*");
            else printf(" ");
        }
        printf("|%d
",a[i]);
 
        printf("+");
        for(ll i=1;i<=len;i++) printf("-");
        printf("+
");
    }
}

---

I

如图，这样构造是最优的。

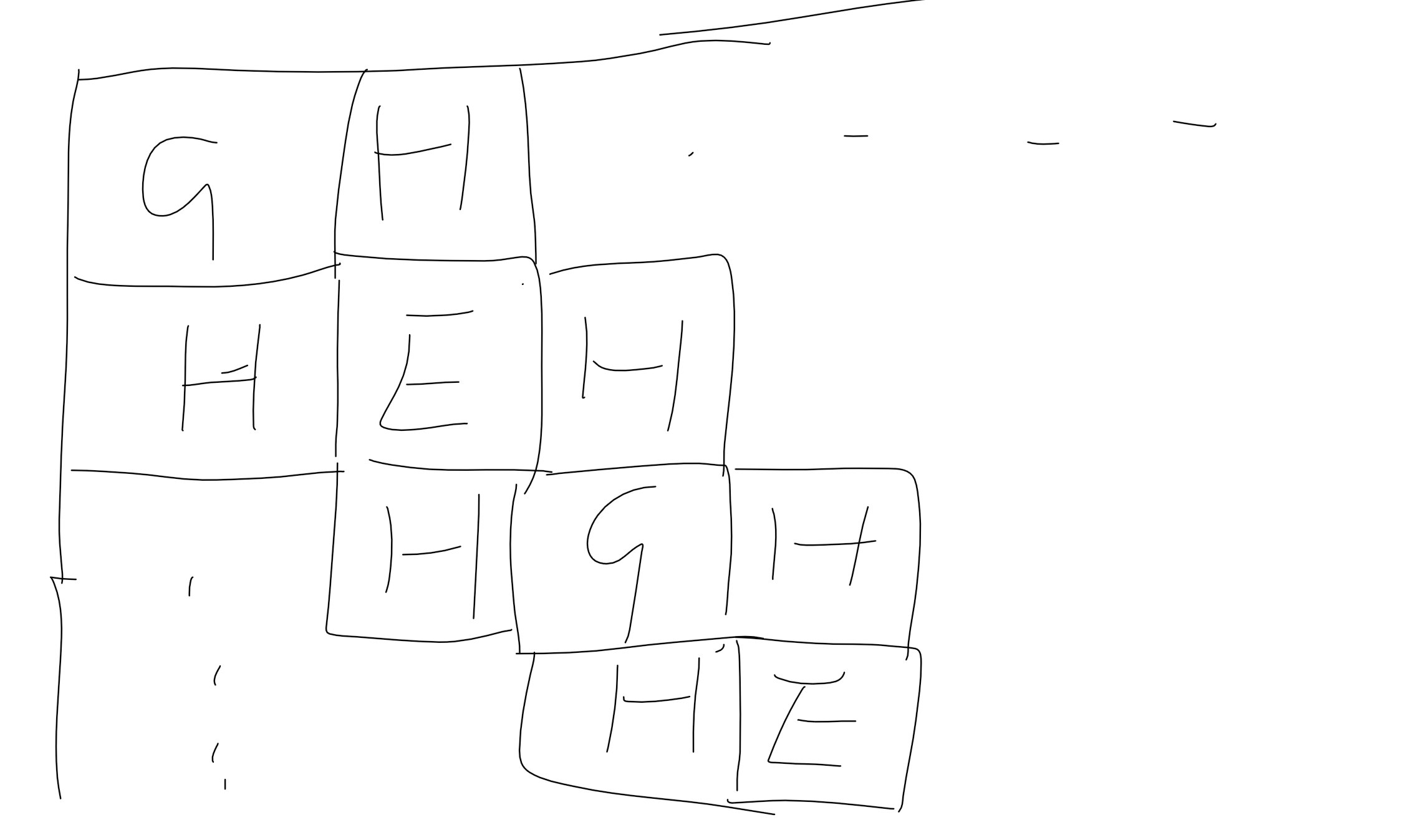
然后把这个对角线上下平移密铺满整个空间就是最终的构造结果，因为这个矩阵是无限大的，所以我们无需考虑边界问题，之间从图中可以看出H的占比是(frac{2}{3})。

#include <bits/stdc++.h>

using namespace std;

#define ll long long
ll input(){
	ll x=0,f=0;char ch=getchar();
	while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
	return f? -x:x;
}

int main(){
	printf("0.666667
");
}

---

E

置换群。题目是求有多少个排列，经过若干次置换(T),之后得到单位置换(e)，不难想到就是求有多少个(e*T^k)，然后(k)最大等于(x)，当满足(T^x=e)时。然后题目就相当于解这个(x),那么处理出置换的每个循环的长度，所有循环的长度求LCM就是答案了，然后由于答案可能非常大，所以要用大数运算来计算答案。

vis = []
cir = []
	
def gcd(a,b):
    if a%b == 0:
        return b
    else :
        return gcd(b,a%b)

def  lcm(a,b):
	return a*b//gcd(a,b)

a = []

tt = []

n = int(input())
tt = list(map(int, input().split()))

t = []
t.append(0)
for i in tt:
    t.append(i)

for i in range(0,n+1):
	vis.append(0)

for i in range(1,n+1):
	x = i
	num = 0
	while vis[x] == 0:
		vis[x] = 1
		x = t[x]
		num += 1
	if num != 0:
		a.append(num)

Ans = 1
for v in a:
	Ans = lcm(Ans, v)

print(Ans)

---

D

由题容易发现两个操作的本质一个是长度为(n)的循环和一个长度为((n-1))的循环。我们不妨把(P)串首尾相连，然后在环上找到一个位置，其合法相对位置最多。最后操作的答案一定是合法相对位置最多的位置中，不合法的位置个数。易知我们只需要取环上的一个最长上升子序列，然后用两个环形成的缓冲区调整不合法数的位置即可。

#include <bits/stdc++.h>

using namespace std;

#define ll long long
ll input(){
	ll x=0,f=0;char ch=getchar();
	while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
	return f? -x:x;
}

const int N=1007;

int b[N],a[N],f[N];
int n;

int work(int pos){
	int cnt=0;
	for(int i=0;i<n;i++){
		a[++cnt]=b[(pos+i)%n];
	}

	int ans=1;f[1]=a[1];
	for(int i=2;i<=n;++i){
		int l=1,r=ans,mid;
		while(l<=r){
			mid=(l+r)>>1;
			if(a[i]<=f[mid])r=mid-1;
			else l=mid+1;
		}f[l]=a[i];
		if(l>ans)++ans;
	}
	return ans;
}

int main(){
	n=input();

	for(int i=0;i<n;i++){
		b[i]=input();
	}

	int Ans=0x3f3f3f3f;

	for(int i=0;i<n;i++){
		Ans=min(Ans,n-work(i));
	}

	printf("%d
",Ans);
}

---

B

由于要保证任意一个环的异或和都是(0),实际上来说每一条边的边权都已经确定了，那么我们把每一条能连的边都连上，就形成了一个完全图。我们不难发现最后的答案一定是最小生成树。由于边的集合非常巨大，所以我们无法直接求最小生成树。我们考虑让权与点有关，我们随意构造一下，随便指定一个节点为根，设该点的权为(0),那么其它点都能推出点权。

然后问题变成了求最小异或生成树。由boruvka算法我们受到启发，两个连通块（也是最小生成树）直接连一条可以连的权值最小的边一定构成最小生成树。异或最小我们可以把所有的点权二进制化放到一个字典树中，那么相同数相连一定是(0)，所以先相同的数直接连，然后在字典树上只要保留一个即可，接下来一个子树一个子树的计算答案，两个不相交的连通块一定是左子树上找一个值与右子树上找一个值异或最小，那么我们只需要枚举较小的子树的值，然后在较大的子树上找最小异或即可。因为我们异或要更小，那么包括它们的子树一定更小（即他们的公共链越长）。故答案一定是在每个两个子树找一条权值最小的边相连。

#include <bits/stdc++.h>

using namespace std;

#define ll long long
ll input(){
	ll x=0,f=0;char ch=getchar();
	while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
	while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
	return f? -x:x;
}

const int N=2e5+10;
const int inf=0x3f3f3f3f;
#define ls ch[now][0]
#define rs ch[now][1]
int L[N*40],R[N*40],ch[N*40][2],tot;
int n,a[N],root;
void Insert(int &now,int x,int dep){
    if(!now) now=++tot;
    L[now]=min(L[now],x),R[now]=max(R[now],x);
    if(dep<0) return;
    int bit=a[x]>>dep&1;
    Insert(ch[now][bit],x,dep-1);
}
int query(int now,int val,int dep){
    if(dep<0) return 0;
    int bit=val>>dep&1;
    if(ch[now][bit]) return query(ch[now][bit],val,dep-1);
    else return query(ch[now][bit^1],val,dep-1)+(1<<dep);
}
ll dfs(int now,int dep){
    if(dep<0) return 0;
    if(R[ls]&&R[rs]){
        int mi=inf;
        for(int i=L[ls];i<=R[ls];i++) mi=min(mi,query(rs,a[i],dep-1));
        return dfs(ls,dep-1)+dfs(rs,dep-1)+mi+(1<<dep);
    }
    if(R[ls]) return dfs(ls,dep-1);
    if(R[rs]) return dfs(rs,dep-1);
    return 0;
}

struct edge{
	ll v,w;
};

vector <edge> G[N];

void ddfs(ll u,ll fa){
	for(auto v:G[u]){
		if(v.v==fa) continue;
		a[v.v]=a[u]^v.w;
		ddfs(v.v,u);
	}
}

int main(){
	ll n=input();

	for(ll i=1;i<n;i++){
		ll u=input(),v=input(),w=input();
		G[u].push_back((edge){v,w}),G[v].push_back((edge){u,w});
	}

	ddfs(0,-1);

	// for(int i=0;i<n;i++) cout<<a[i]<<" ";cout<<endl;

	sort(a+1,a+1+n);
    memset(L,0x3f,sizeof(L));
    for(int i=1;i<=n;i++) Insert(root,i,30);
    printf("%lld
",dfs(root,30));
    return 0;
}

---

A

动态规划。

首先显然我们可以把任务拆分为(2*k)个目标路点，问题转化为在图上依次经过2*k个目标路点，并且可以使用传送枪，使得答案最小。

我们首先可以考虑一个非常麻烦的动态规划，(dp[i][u][a][b])表示当前已经经过了(i)个路点，当前在(u)点上，并且门连通(a)和(b)。这个转移是有环的。那么我们对于每一次转移可以考虑用dijkstra跑出最短路树，然后在最短路树上转移u就是最优，且没有环了。

我们经过研究发现，如果我们要使用门，存储门的入口是没有意义的，因为我们只要使用遥控器的清空门的入口，再往地上打一枪，就覆盖了所有使用传送门的情况了。所以动态规划变成了(dp[i][u][p])。

从上一步我们发现我们需要在图上进行转移，我们的最终目标是增加(i)到(2*k)并且中间许多转移对增加(i)并没有贡献。那么我们只需要讨论从上一个路点到下一个路点的最优的答案是什么，因此我们可以提前用floyd预处理所以点到其它所有点的距离。现在我们考虑的动态规划转化为(dp[i][p])。那么我们只需要考虑三种转移即可。

我们不妨设第(i)个路点为(d[i])。

第一种转移，我们设当前传送出口为(p)我们直接前往下一个路点那么转移为：

[dp[i][p]=min(dp[i][p],dp[i-1][p]+dis[d[i-1]][d[i]]) ]

第二种转移，我们设当前传送出口为(p)，我们要把传送出口转变为(q)，那么我们可以先从当前(d[i-1])前往(q)点，再通过传送门前往(p)点，再前往(d[i])点，转移为：

[dp[i][q]=min(dp[i][q],dp[i-1][p]+dis[d[i-1]][q]+dis[p][d[i]]) ]

第三种转移，我们设当前传送出口为(p)，我们要把传送出口转变为(q)，那么我们可以先通过传送门从当前(d[i-1])前往(p)点，再前往(q)点，再前往(d[i])点，转移为：

[dp[i][q]=min(dp[i][q],dp[i-1][p]+dis[p][q]+dis[q][d[i]]) ]

复杂度是(O(kn^2+n^3))的。

#include <bits/stdc++.h>
 
using namespace std;
 
#define ll long long
ll input(){
    ll x=0,f=0;char ch=getchar();
    while(ch<'0'||ch>'9') f|=ch=='-',ch=getchar();
    while(ch>='0'&&ch<='9') x=x*10+ch-'0',ch=getchar();
    return f? -x:x;
}
 
const int N=307;
 
ll dis[N][N];
ll dp[N*2][N];
ll d[N*2];
int n,m,k;
 
void init(){
    for(int l=1;l<=n;l++){
        dis[l][l]=0;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                dis[i][j]=min(dis[i][l]+dis[l][j],dis[i][j]);
            }
        }
    }
}
 
int main(){
    memset(dis,0x3f,sizeof dis);
    n=input(),m=input(),k=input();
 
    for(int i=1;i<=m;i++){
        ll u=input(),v=input(),w=input();
        dis[u][v]=min(dis[u][v],w);
        dis[v][u]=min(dis[v][u],w);
    }
 
    for(int i=1;i<=2*k;i+=2) d[i]=input(),d[i+1]=input();
 
    init();
    memset(dp,0x3f,sizeof dp);
 
    for(int i=1;i<=n;i++) dp[0][i]=dis[1][i];
    d[0]=1;
 
    for(int i=1;i<=2*k;i++){
        for(int p=1;p<=n;p++){
            dp[i][p]=min(dp[i][p],dp[i-1][p]+dis[d[i-1]][d[i]]);
            for(int q=1;q<=n;q++){
                dp[i][q]=min(dp[i][q],dp[i-1][p]+dis[d[i-1]][q]+dis[p][d[i]]);
                dp[i][q]=min(dp[i][q],dp[i-1][p]+dis[p][q]+dis[q][d[i]]);
            }
        }
    }
 
    ll Ans=0x3f3f3f3f3f3f3f;
    for(int i=1;i<=n;i++){
        Ans=min(Ans,dp[2*k][i]);
    }
 
    printf("%lld
",Ans);
}