B: 最小代价

B: 最小代价

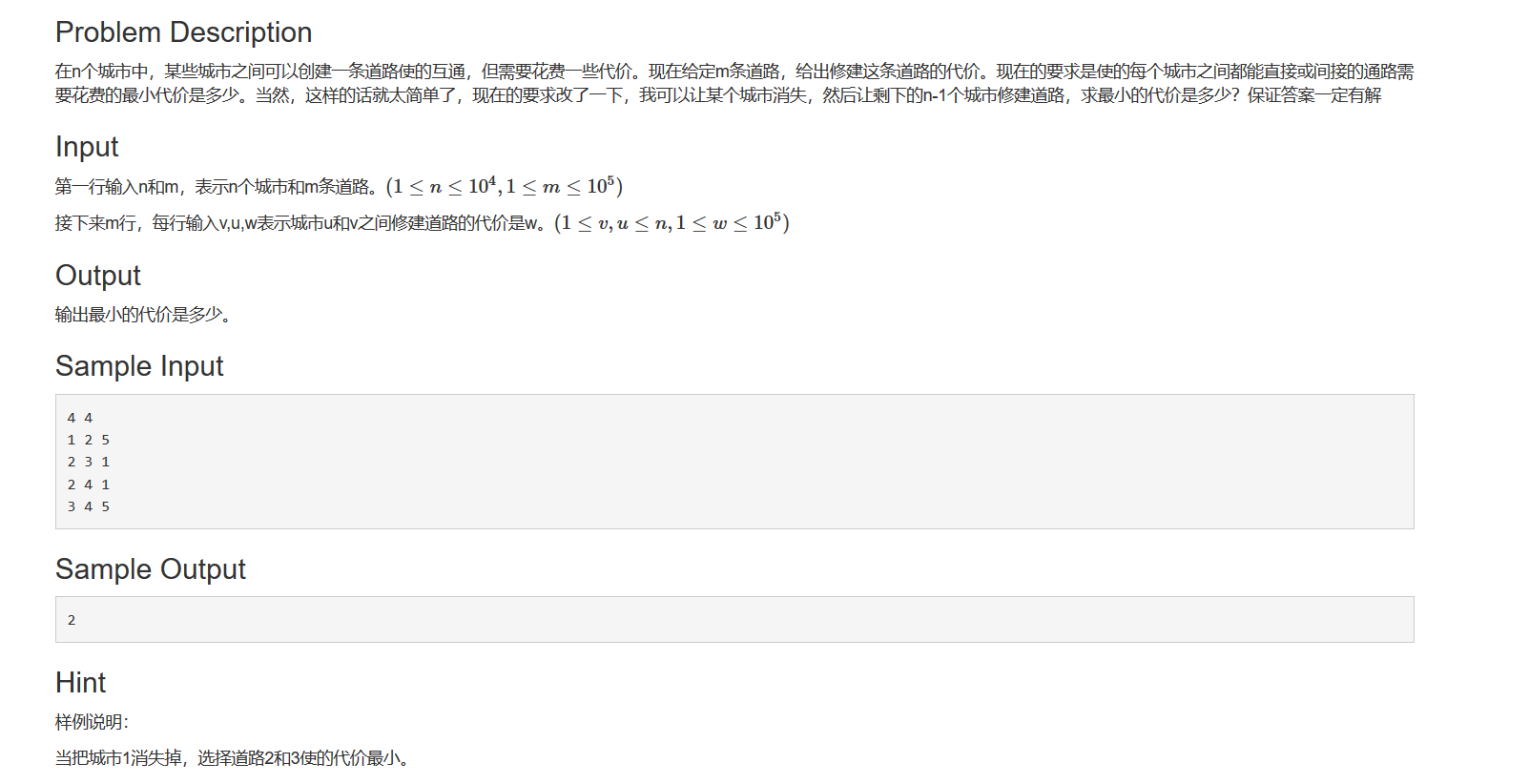
题解：先用最小生成树求联通所有点的最小代价ans

在求度为1的时候权值最大的点mx

ans-mx就是答案

#include<iostream>
#include<algorithm>
#include<vector>
#include<math.h>
#define ll long long
using namespace std;
int p[100005],r[100005];
int n,m;
ll ans=0;
vector<int>du[100005];//计算度
struct node
{
  int x;//x,y是坐标，v是权值
  int y;
  int v;
}a[100005];
bool cmp(node b,node c)
{
  return b.v<c.v;
}
int find(int x)//查找元素x的老板是谁
{
    if (x == p[x])
        return x;
    else
        return p[x] = find(p[x]);
}

void join(int x, int y)//路径压缩合并两个集合
{
    int xRoot = find(x);
    int yRoot = find(y);

    if (xRoot == yRoot) //老板相同，不合并
        return;
    //cnt=cnt-1;
    if (r[xRoot] < r[yRoot]) //r[i]是元素i所在树的高度，矮树的根节点认高树的根节点做老板
        p[xRoot] = yRoot;
    else if (r[xRoot] > r[yRoot])
        p[yRoot] = xRoot;
    else
    {
        p[yRoot] = xRoot;//树高相同，做老板的树高度要加一
        r[xRoot]++;
    }
}
void kruskal()
{
  for(int i=1;i<=n;i++)//初始化根节点
    p[i]=i;
  sort(a+1,a+m+1,cmp);
  for(int i=1;i<=m;i++)
  {
    if(find(a[i].x)!=find(a[i].y))
    {
      join(a[i].x,a[i].y);
      ans=ans+a[i].v;
      du[a[i].x].push_back(a[i].v);
      du[a[i].y].push_back(a[i].v);
    }
  }
}
int main()
{
    cin>>n>>m;
    for(int i=1;i<=m;i++)
        cin>>a[i].x>>a[i].y>>a[i].v;
    kruskal();
    int  mx=0;
    for(int i=1;i<=n;i++)
        if(du[i].size()==1)//找度为一且权值最大的点
            mx=max(mx,du[i][0]);
    cout<<ans-mx<<endl;
    return 0;
}