第1课 算法的时间复杂度

判断一个算法的效率时，操作数量中的常数项和其他次要项常常可以忽略，只需要关注最高阶项就能得出结论。（这只是定性的比较）

问题：如何用符号定性的判断算法的效率？

算法的复杂度
-时间复杂度
　　算法运行后对时间需求量的定性描述
-空间复杂度
　　算法运行后对空间需求量的定性描述

注意：
数据结构课程重点关注的是算法的效率问题，因此，整个课程会集中于讨论算法的时间复杂度，但其使用的方法完全可以用于空间复杂度的判断

大O表示法
-算法效率严重依赖于操作（operation）数量
-操作数量的估算可以作为时间复杂度的估算
-在判断时首先关注操作数量的最高次项
O(5) = O(1)
O(2n+1) = O(2n) = O(n)
O(n*n + n + 1) = o(n*n)
O(3*n*n*n +1 )= O(3*n*n*n) =O(n*n*n)

常见的时间复杂度

线性阶时间复杂度：O(n)
for(int i=0; i<n; i++)
{
　　//复杂度为O(1)的程序语句
}
循环次数：n

对数阶时间复杂度：O(logn)
int i =1;
while(i<n)
{
　　//复杂度为O(1)的程序语句
　　i*= 2
}
循环次数：log2n(这个地方是以2为底哦)

平方阶时间复杂度：O(n*n)
for(int i=0; i<n; i++)
{
　　for(int j=0; j<n; j++)
　　{
　　　　//复杂度为O(1)的程序语句
　　}
}
循环次数：n*n

时间复杂度计算练习一
下面代码的时间复杂度是什么？
for(int i=0; i<n; i++)
{
　　for(int j=i; j<n; j++)
　　{
　　　　//复杂度为O(1)的程序语句
　　}
}

时间复杂度计算练习二

函数func()的时间复杂度是什么？
void func(int n)
{
　　int i =0;
　　while(i< n)
　　{
　　　　t(n);
　　　　i++;
　　}
}

void t(int n)
{
　　int i=0;
　　while(i<n)
　　{
　　　　cout << i <<endl;
　　}
}

时间复杂度计算练习三

函数test()的时间复杂度是什么？
void test(int n)
{
　　t(n);
　　for(int i=0; i<n; i++)
　　{
　　　　t(i);
　　}

　　for(int i=0; i<n; i++)
　　{
　　　　for(int j=i; j<n; j++)
　　　　　　t(i);
　　}
}

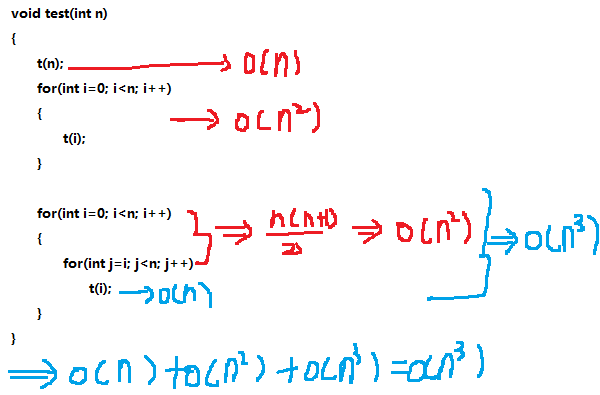
小结：
时间复杂度是算法运行时对于时间的需求量
大O表示法用于描述算法的时间复杂度
大O表示法只关注操作数量的最高次项
常见的时间复杂度为：线性阶，平方阶和对数阶