Description
Asterix,Obelix和他们的临时伙伴Suffix、Prefix已经最终找到了和谐寺。然而和谐寺大门紧闭,就连Obelix的运气也没好到能打开它。
不久他们发现了一个字符串S(|S|<=1000000),刻在和谐寺大门下面的岩石上。Asterix猜想那一定是打开寺庙大门的密码,于是就大声将字符串朗读了出来,然而并没有什么事发生。于是Asterix又猜想密码一定是字符串S的子串T。
Prefix认为T是S的前缀,Suffix认为T是S的后缀,Obelix却认为T应该是S中的某一部分,也就是说,T既不是S的前缀,也不是S的后缀。
Asterix选择子串T来满足所有伙伴们的想法。同时,在所有可以被接受的子串变形中,Asterix选择了最长的一个(因为Asterix喜欢长的字符串)当Asterix大声读出子串T时,寺庙的大门开了。 (也就是说,你需要找到既是S的前缀又是S的后缀同时又在S中间出现过的最长子串)
现在给你字符串S,你需要找到满足上述要求的子串T。
Input
一个长度在[1,1000000]间的只包含小写字母的字符串S。
Output
输出子串T,如果T不存在,输出 "Just a legend",不包含引号。
一句话题意
求一个给定串(s)的一个子串(T).
满足
- (T)是(s)的前缀
- (T)是(s)的后缀
- (T)在(s)中间出现过
xjb分析
首先明确我们要找的是这种情况.

此时,我们发现,蓝色部分好像是什么东西?
(KMP)算法中的(next)! (最长公共前后缀的长度
现在明确了我们的解题方法,(KMP)
那么现在的问题就是要找图中红色部分.
如何去找红色部分?
我们发现,可以将图片看成这样.
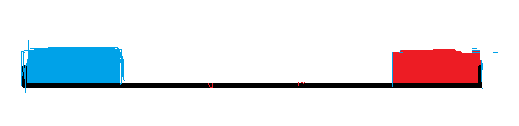
这样又成了(KMP)算法中的(next)
那么现在我们需要知道最长的长度.
显然,中间部分的长度可能比(s)的前缀或后缀长亦可能短,但是长度最大只可能是(next[n]).
即真实答案(ans leq next[n])
所以我们需要在$2 (到)n-1(中找到第一个比)next[n]$小的位置。
而,我们需要记录一下(mxx=sum_{i=2}^{n-1}next_i)
有什么用?
考虑一下我们的中间部分的子串长度只可能是(leq next[n])的,因此我们要一直跳转(next[n])知道某个位置小于等于中间部分最长子串的长度.
这个时候问题得以解决.
判断无解的话只需要判断跳转到的(next)是否为(0)输出(Just a legend)即可。
最后只需要枚举(i)从(2)到(n-1)去找那个(next[i])即可.
然后直接输出即可.
代码
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#define R register
using namespace std;
char s[1000080];
int len,nex[1000080],k,mxx,now;
inline void judge()
{
if(!now)
{
puts("Just a legend");
exit(0);
}
}
int main()
{
scanf("%s",s+1);
len=strlen(s+1);nex[1]=0;
for(R int i=2;i<=len;i++)
{
while(k and s[k+1]!=s[i])k=nex[k];
if(s[i]==s[k+1])k++;
nex[i]=k;
if(i!=len)mxx=max(nex[i],mxx);
}
now=nex[len];
judge();while(now>mxx)now=nex[now];judge();
for(R int i=2;i<len;i++)
if(now==nex[i])
{
for(R int j=i-now+1;j<=i;j++)
printf("%c",s[j]);
exit(0);
}
}