7.14 单调栈 单调队列 +dp优化

单调栈和单调队列的定义具体看ppt了

模板：

单调队列

    head =1; tail = 0;
    rep( i ,1 ,n ){
        while( head <= tail && a[i] < dq[tail].first)tail--;
        while( head <= tail && dq[head].second < i-k+1) head++;
        dq[ ++tail ]={a[i] ,i};    

例题：https://vjudge.net/contest/310230#problem/B

求滑动窗口内最大(小)值

单调栈

    for( ll i=1 ;i<=n ;i++ ){
        while( tail >0 &&  q[tail].first>=a[i] ) tail--;
        l[i] = q[tail].second;
        q[++tail] = {a[i] ,i};
    }

例题：https://vjudge.net/contest/310230#problem/A

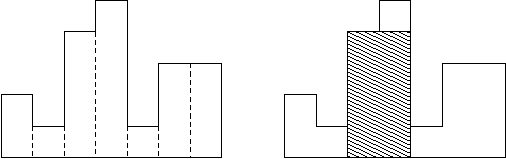
求柱状图内最大矩形面积

dp优化：

1.https://vjudge.net/contest/310230#problem/D

n

n 个木板，mm 个粉刷匠，每块木板最多刷一次，第 ii 个粉刷匠要么不刷，要么刷包含 木板 SiSi​ 的、长度不超过 LiLi​ 的连续一段木板，每刷一块得到 PiPi​ 的钱，求最大能一共能获得多少钱。

 暂时写不出来 ，参考博客：https://blog.csdn.net/j2_o2/article/details/88963367

#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
#include<queue>
#define rep( i ,x ,y) for( int i=x ;i<=y ;i++ )
using namespace std;
struct Node{
    int l ,p ,s;
    bool operator < ( const Node & rsh )const{
         return s < rsh.s;
    }
}e[150];

int dp[105][20000] ,q[20000]; 

int res( int i ,int k){
    return dp[i-1][k] - e[i].p*k;
}

int main(){
    int m ,n;
    while( ~scanf( "%d%d" ,&n ,&m) ){
        rep( i ,1 ,m )
            scanf("%d%d%d" ,&e[i].l ,&e[i].p ,&e[i].s);
        sort( e+1 ,e+1+m );
        rep( i ,1 ,m ){
        
            int head = 1 ,tail = 0;
            rep( j ,max( 0 ,e[i].s-e[i].l) ,e[i].s-1 ){
                while( head<=tail && res(i ,j) >= res(i ,q[tail])) tail--;
                q[ ++tail ] = j;    
            }
            
            rep( j ,1 ,n ){
                dp[i][j] = max( dp[i-1][j] ,dp[i][j-1] );
                if( j >= e[i].s ){
                    while( head <= tail && q[head] < j-e[i].l ) head++;
                    if( head <= tail )dp[i][j] = max( dp[i][j] ,res( i, q[head] )+e[i].p*j );
                }
            }
        }
        printf( "%d
" ,dp[m][n] );
    }
    return 0;
}