机器学习十讲第八讲

什么是维度灾难？

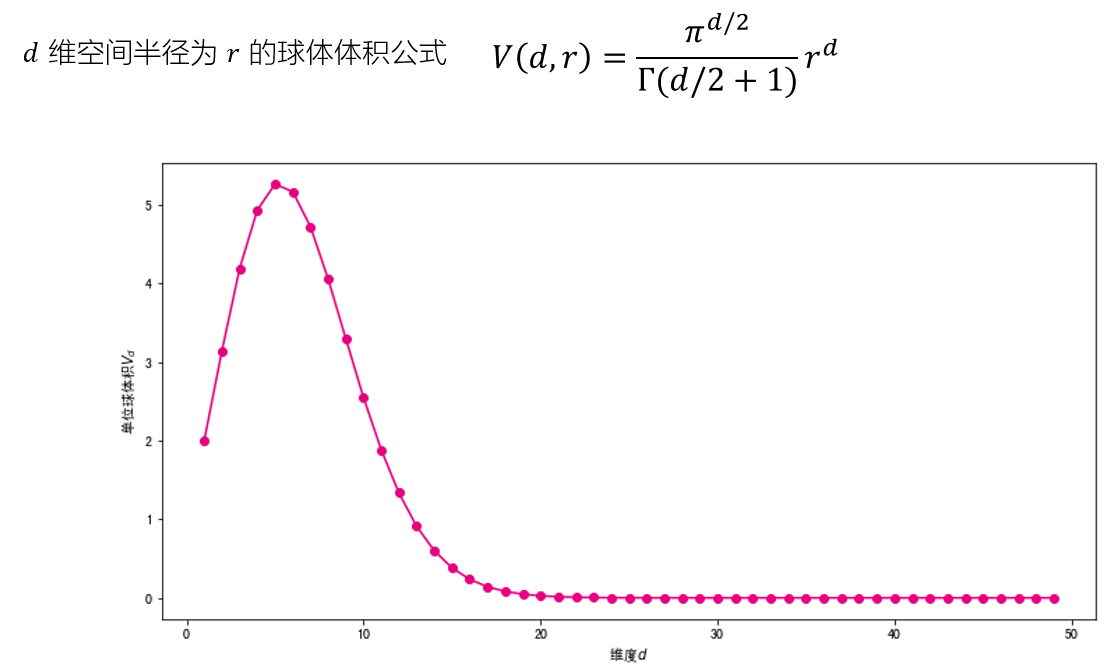
高维空间的反直觉示例：单位球体积

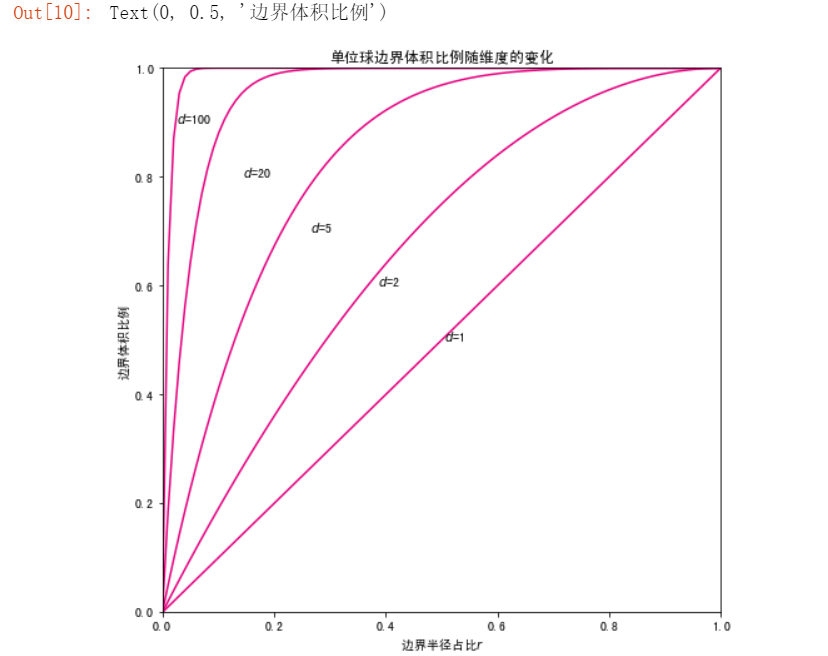
单位球体积随维数的变化

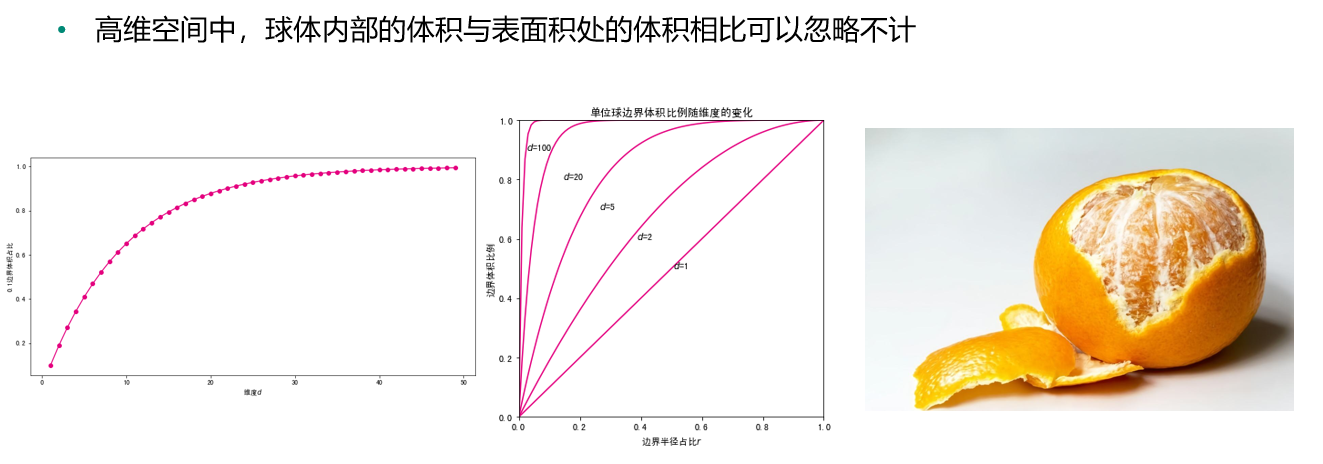
边界体积占比变化

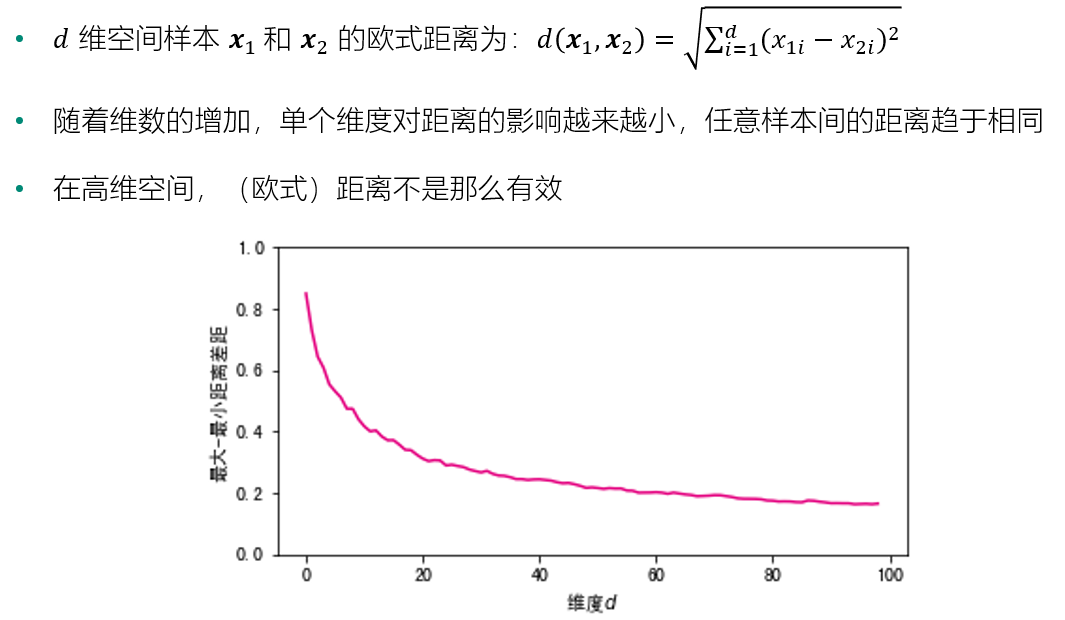
高维空间中的欧式距离

基于距离的机器学习模型

• K近邻：样本间距离
• 支持向量机：样本到决策面距离
• K-Means ：样本到聚类中心距离
• 层次聚类：不同簇之间的距离
• 推荐系统：商品或用户相似度
• 信息检索：查询和文档之前的相似度

 

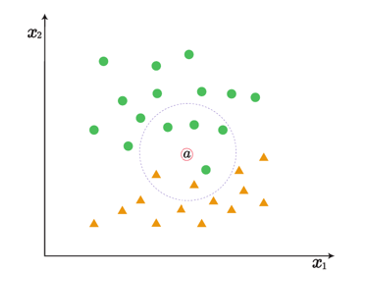
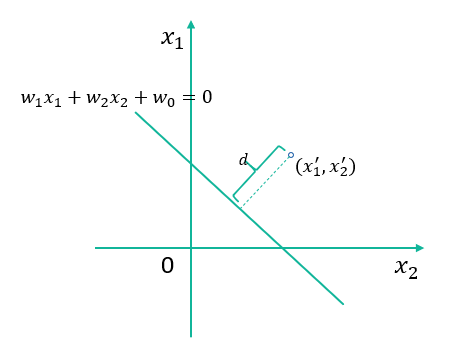
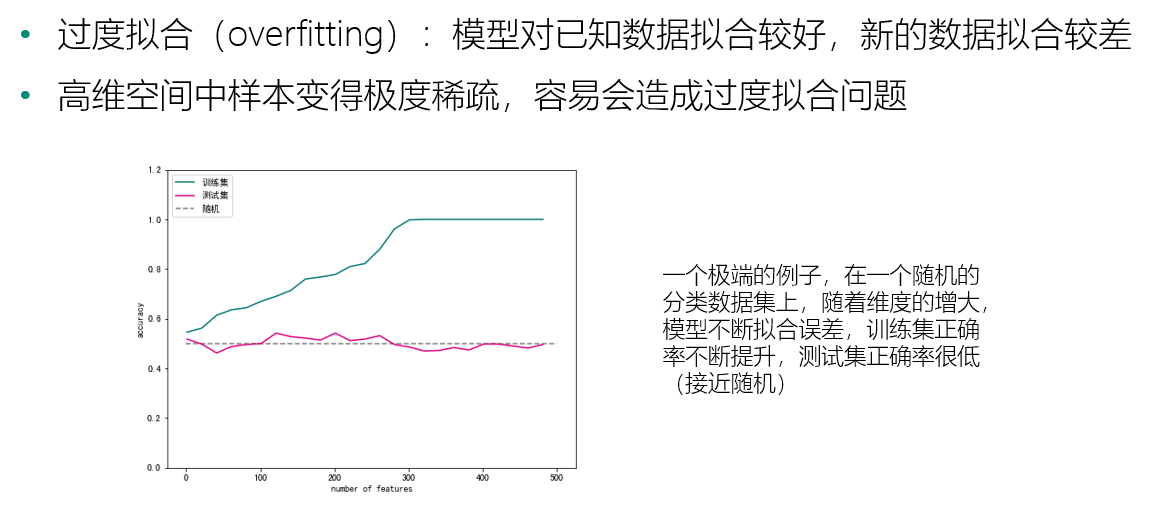
稀疏性与过度拟合

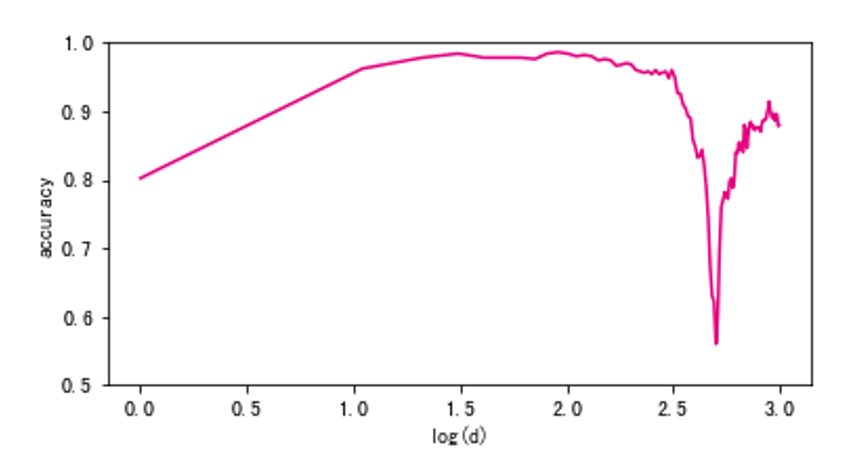
Hughes 现象

• 1968年，Hughes 发现在训练集固定时，随着维度的增大，分类器性能不断提升直到达到最佳维度，继续增加维度分类器性能会下降

计算复杂度：决策树

计算复杂度：朴素贝叶斯

 

应对维度灾难：特征选择和降维

应对维度灾难：过度拟合与正则化

应对维度灾难：核技巧

案例——使用Python认识维度问题。

#公式实现
import numpy as np
import math
#引用伽马函数
from scipy.special import gamma
def V(d,r):
    return math.pi**(d/2)*(r**d)/gamma(d/2 + 1)
#测试一下
print(V(1,1))

#将单位球体积随着维度的变化进行可视化
##为了方便观察，设置维度为1-70
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 6)) #设置图片大小
ds = np.arange(1,70)
plt.plot(ds,V(ds,1),color="#E4007F",marker="o")
plt.xlabel("维度$d$")
plt.ylabel("单位球体积$V_d$")

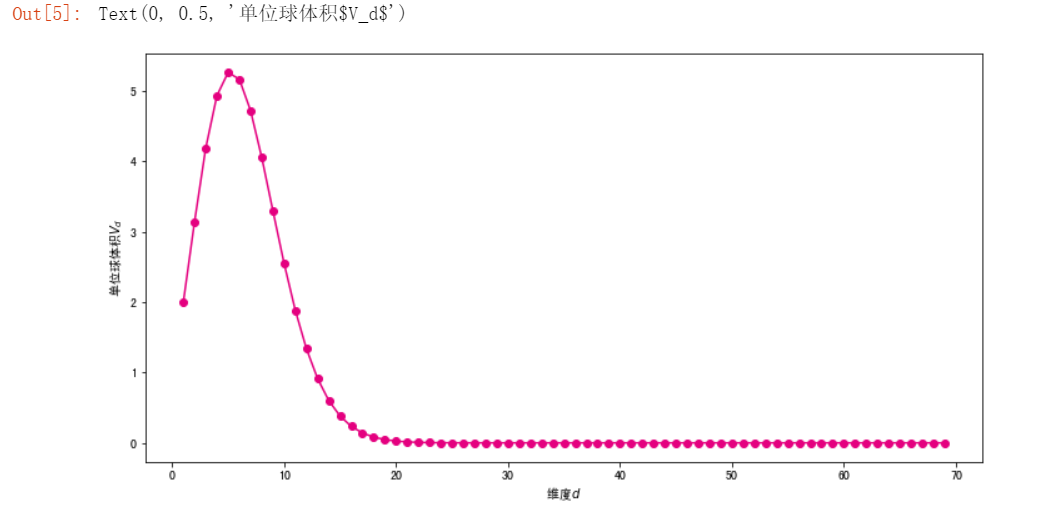
#看一下0.1半径体积的比例是多少
##假设边界为0.1
def ratio(d):
    return (V(d,1) - V(d,0.9))/ V(d,1)
df["ratio90"] =  1 - 0.9**(df.d)
df.round(6).head(20)

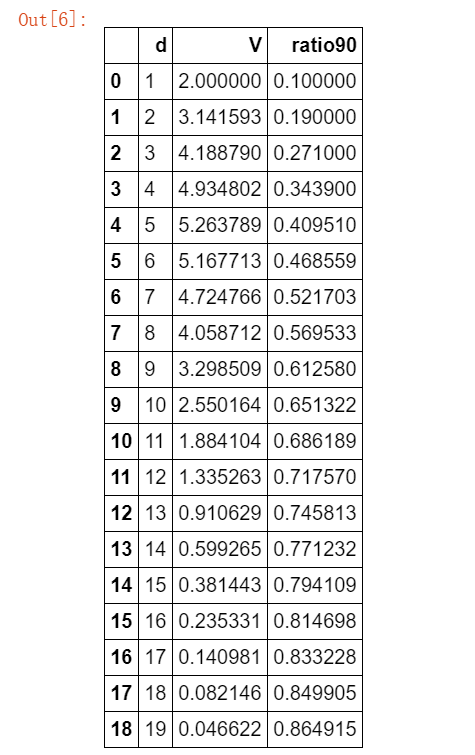
#将0.1边界体积比例可视化
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(12, 6)) #设置图片大小
ds = np.arange(1,50)
plt.plot(ds,ratio(ds),color="#E4007F",marker="o")
plt.xlabel("维度$d$")
plt.ylabel("0.1边界体积占比")

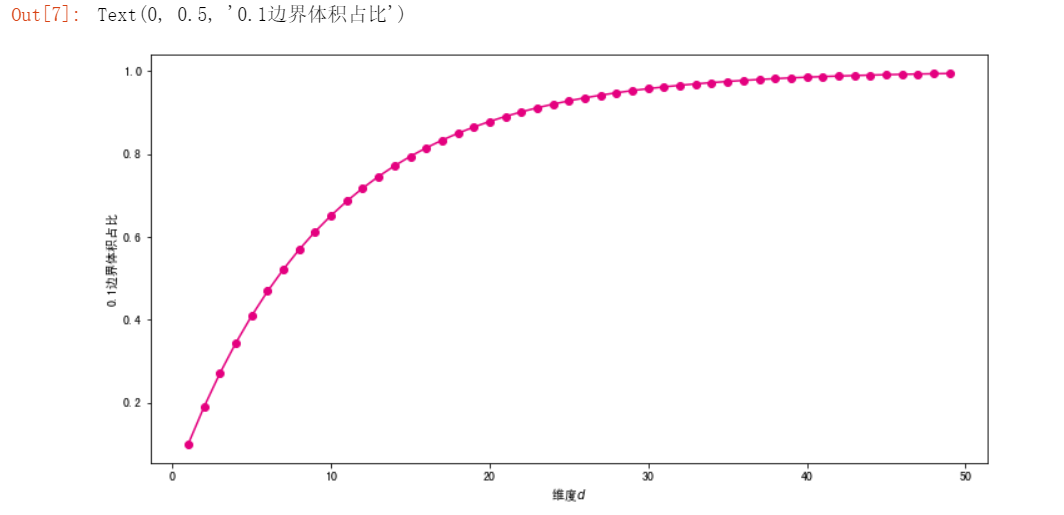
#刚才的方法是指定边界为0.1，为了能查看任意边界比例的情况，再写一个方法
def volumn_fraction_in_border(d,r):
    return(V(d,1)-V(d,1-r))/V(d,1)
#可视化
import numpy as np
#设置维度
ds=[1,2,5,20,100]
#设置颜色
colors=["gray","#E4007F","","","",""]
rs=np.linspace(0,1,100)
result=[]
for d in ds:
    vs=[]
    for r in rs:
        vs.append(volumn_fraction_in_border(d,r))
    result.append(vs)
import matplotlib.pyplot as plt
%matplotlib inline
fig, ax = plt.subplots(figsize=(8, 8)) #设置图片大小
plt.title("单位球边界体积比例随维度的变化")
for i in range(len(ds)):
    plt.plot(rs,result[i],color="#E4007F",label="d="+str(ds[i]))
    plt.text(rs[50]-i*0.12,0.5+i*0.1,"$d$="+str(ds[i]))
plt.xlim(0,1)
plt.ylim(0,1)
plt.xlabel("边界半径占比$r$")
plt.ylabel("边界体积比例")