本周学习总结
1.思维导图
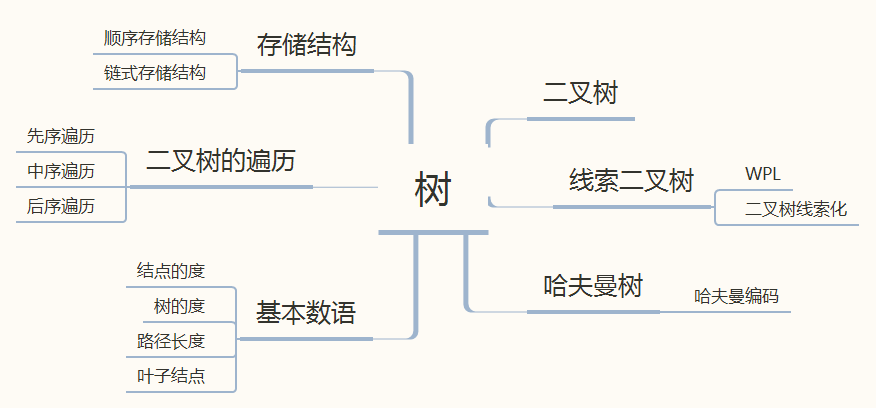
2.谈谈你对树结构的认识及学习体会。
树,整体来说,我依然很薄弱。pta,简单题对着书敲一敲还可以,一边敲,一边背,但说实话,这都是短时记忆,总是不那么牢靠,先理解,在记忆,我也常常会出现许多状况,就单是上机考试里出现dev运行结果都是对的,pta却过不了的状况,实属让人手忙脚乱,反复确认自己的记忆没出现问题,确认思路也无什么问题。其实这些东西不过是小小的没有赋初始值。大作业在编写代码上我并没有参与,我不过是对于组员的劳动成果进行理解罢了,我深知自己实力不够,对于代码的看懂我都需要询问当事人,再细细理解。
2.PTA实验作业
2.1.还原二叉树
2.1.1设计思路(伪代码)
- main函数
定义n,h,pre[50],in[50],T
输入 n,pre,in
T=CreatTree(pre,in,n);
h=GetHeight(T);
输出 h
- 建树
定义 T,*p, k
if(n<=0) return NULL
建立T的节点空间
T->data=*pre
for(p=in;p<in+n;p++)
if(*p==*pre) break
k=p-in
T->lchild=CreatTree(pre+1,in,k)
T->rchild=CreatTree(pre+k+1,p+1,n-k-1)
返回T
- 高度
定义LH, RH;
if(T==NULL)
return 0;
LH = GetHeight(T->lchild)
RH = GetHeight(T->rchild)
返回LH > RH ? ++LH : ++RH
2.1.2代码截图



2.1.3本题PTA提交列表说明。
- 最开始在pta上打代码,打了一般,就先提交保存了,所以编译错误
- 建树的递归有一些问题,最开始直接运用T->lchild=CreatTree( s, 2 * i)这个,但是建的不对,最后借鉴了一下别人的方法,改正了一下
2.2 二叉树叶子结点带权路径长度和
2.2.1设计思路(伪代码)
- 建树
if (i<s.length())
if (s[i] == '#')
T = NULL
else
T 建立节点空间
T->data = s[i]
T->lchild=CreatTree( s, 2 * i)
T->rchild=CreatTree( s, 2 * i + 1)
else T = NULL;
返回T
- 路径
if T为空 sum+0
else
if (!T->lchild && !T->rchild)
sum += (T->data - '0')*i
CountWPL(sum, T->lchild,i+1) //递归
CountWPL(sum, T->rchild,i+1)
- main函数
定义字符串s,树T,整数sum
输入s
sum赋值0
T=CreatTree(s, 1)
CountWPL(sum, T,0)
输出sum
2.2.2代码截图
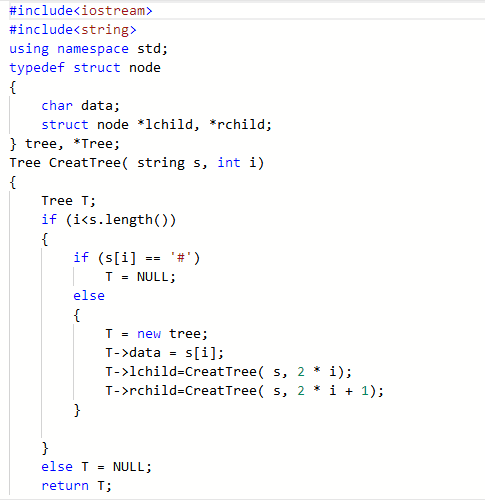
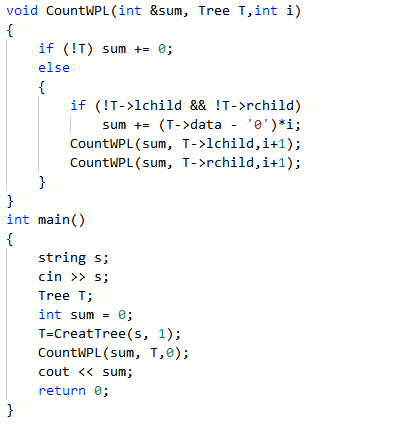
2.2.3本题PTA提交列表说明。
- 起先是照着答案敲的
- 自己背了,理解了,重新敲了一下,但是sum没赋值,答案错误
2.3 输出二叉树每层节点
2.3.1设计思路
- 建树
if (i<s.length())
if (s[i] == '#')
T = NULL
else
T 建立节点空间
T->data = s[i]
T->lchild=CreatTree( s, 2 * i)
T->rchild=CreatTree( s, 2 * i + 1)
else T = NULL;
返回T
- main函数
定义字符串s,树T,整数i
输入s
i赋值为0
建father,child队列
T=CreatTree(s, 1)
if(T)
输出i和相应格式
父亲队进队
i++;
else
输出NULL
while(!father.empty())
if(father.front()->lchild)
child.push(father.front()->lchild)
if(father.front()->rchild)
child.push(father.front()->rchild)
输出father.front()->data和相应格式
出队
if(father.empty())
if(!child.empty())
输出i和相应格式
while(!child.empty())
将孩子进父亲的队
出队
i++
2.3.2代码截图

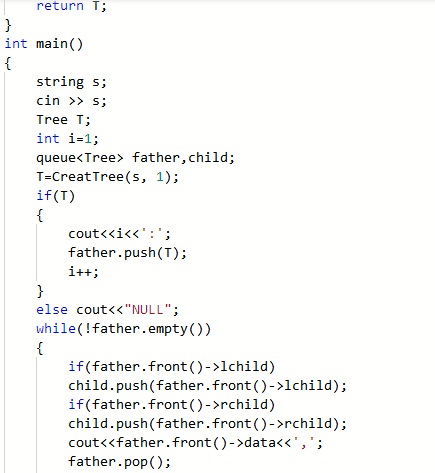
2.3.3本题PTA提交列表说明。
- 这是直接对着答案并记忆以后,对着dev敲,运行成功后提交的
3、阅读代码
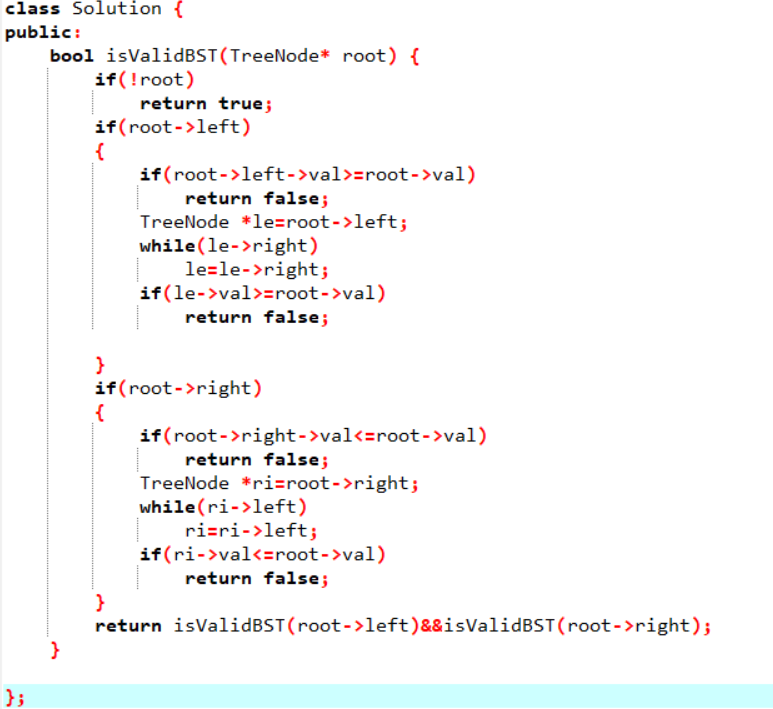
3.1 检验二叉搜索树


3.2 解题思路
- 先判断树为空的情况
- 左子树
- 判断左子树的元素与根元素的大小
- 再进行以左子树作为根的,其右子树的大小判断
- 右子树
- 判断右子树的元素与根元素的大小
- 再进行以右子树作为根的,其左子树的大小判断
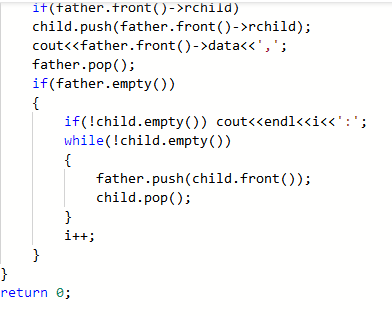
3.3 代码截图
3.4 学习体会
题目不是特别难的题目,方法也比较直接。但是这是我看到的这题代码中,我可以直接看懂,并觉得自己写,也会朝着这方面写的的代码。其中,左右子树与跟之间的判断这一步骤让我受益匪浅。又一次了解了孩子节点转化为相应的根节点这一步骤。