Github项目地址
https://github.com/071703323fei/071703323
我的PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(小时) | 实际耗时(小时) |
| Planning | 计划 | 1 | 1 |
| Estimate | 估计这个任务需要多少时间 | 1 | 1 |
| Development | 开发 | 1 | 1 |
| Analysis | 需求分析 (包括学习新技术) | 4 | 6 |
| Design Spec | 生成设计文档 | 1 | 0.5 |
| Design Review | 设计复审 | 1 | 0.5 |
| Coding Standard | 代码规范 (为目前的开发制定合适的规范) | 0.5 | 0.5 |
| Design | 具体设计 | 1 | 2 |
| Coding | 具体编码 | 3 | 5 |
| Code Review | 代码复审 | 1 | 5 |
| Test | 测试(自我测试,修改代码,提交修改) | 1 | 3 |
| Reporting | 报告 | 1 | 1 |
| Test Repor | 测试报告 | 1 | 1 |
| Size Measurement | 计算工作量 | 0.5 | 0.5 |
| Postmortem & Process Improvement Plan | 事后总结, 并提出过程改进计划 | 0.5 | 0.5 |
| 合计 | 18.5 | 25.5 |
解题过程
开始思路:回溯法求解数独。建立结构体node用来存储每个格子的状态参数,行数,列数,格上数值,和数组v[10],其中v[0]记录所有候选解个数,
v[i](i=1-9):记录i是否为候选解,(i=0是,i=1不是),共计81格。
struct node
{
int row;
int col;
int value;
int v[10]={0}; //v[0]候选数,v[i]=0(可候选)
}no[81]; //no[?]:?=9*x+y
预处理:对所有非0格,使用init(int x,int y)函数,更新该格子对行、列、宫中其他格子的候选数字的影响。
void count(int x,int y)
{
no[9*x+y].v[0]=0;
for(int i=1;i<=9;i++)
{
if(no[9*x+y].v[i]==0) //可候选个数
{
no[9*x+y].v[0]++;
}
}
}
void init(int x,int y,int vv) //扫描方圆几里,更新参数 ,注意vv不可为0
{ //vv为该格子的值
for(int i=0;i<9;i++)
{
no[9*x+i].v[vv]=1; //改为不可候选状态(1)
no[9*i+y].v[vv]=1;
}
int xs,ys;
xs=x/3*3;
ys=y/3*3;
for(int i=xs;i<xs+3;i++)
{
for(int j=ys;j<ys+3;j++)
{
no[9*i+j].v[vv]=1;
}
}
for(int i=0;i<9;i++)
{
count(i,y);
count(x,i);
}
for(int i=xs;i<xs+3;i++)
{
for(int j=ys;j<ys+3;j++)
{
count(i,j);
}
}
}
开始算法:从第一个空格起,用houxuan()函数找到其最小候选解试填入,用init()函数更新影响,对第二个空白格执行第一步,当出现空白格的候选解个数为0时,证明上一步所填不合适,撤销填充及因填充造成的影响,即回溯,直到填满所有空白格。每步填入一个空白格,需更新其所在行、列、宫因其填入造成的影响。
实现方法:开辟两个栈,栈q存放所有填入的空白格,栈s按从右上到左下顺序,存放待填入空格,每次探查s栈栈顶元素是否候选者为空,不空则取出填上并放入q栈,若空,则从q栈中取出栈顶元素,更改填入值后放回,没有候选值则放入q栈。
Houxuan()函数:从v[1]扫描至v[9],有候选者返回最小,无候选则返回-1,
int houxuan(int x,int y)
{
if(no[9*x+y].v[0]==0)
return -1; //候选数字个数为0,返回-1
else
{
for(int i=1;i<=9;i++)
{
if(no[9*x+y].v[i]==0) return i; //返回最小的候选数字
}
}
}
Init(int x,int y)函数:更改行、列、宫内每个格子因(x,y)格子填入造成的候选数字变化
trace()函数:更改因撤回格子给其他格子带来的变化,后来发现,简单粗暴的将行、列、宫中所有格子,该撤回值处的标记从不可候选改为可候选,这样不可行,需要另加test()函数
test()函数:重新扫描并统计每个空白格的候选数字。
单元测试:
1.init()和count()函数的测试,init()后,空白格处计算count()并打印候选数字个数。
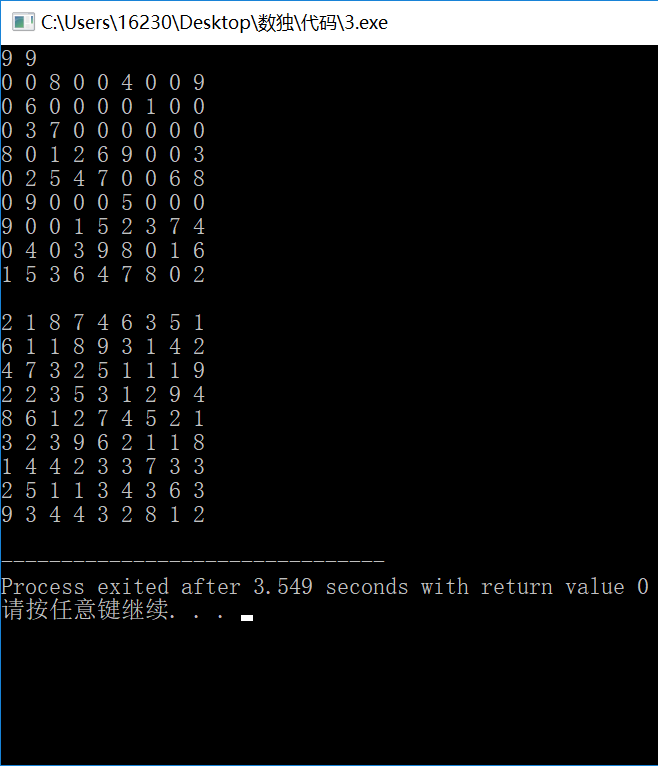
2.对trace()函数测试,每填入一个空白格,打印处状态更新后的表盘,发现程序可回溯,但回溯后影响不可消除,如(0,3)填入后,第0行所有空格的v[5]均为1(不可候选),但回溯时将5撤回,(0,0)的v[5]仍为不可候选,导致回溯至(0,0)时,唯一两个候选者,用去2后5不可用,程序失败。证明trace()函数有问题,反复核查改进后,仍不可正确运行,查阅资料发现回溯应用深搜dfs实现,深搜有点问题,决定更换思路,重新来过。
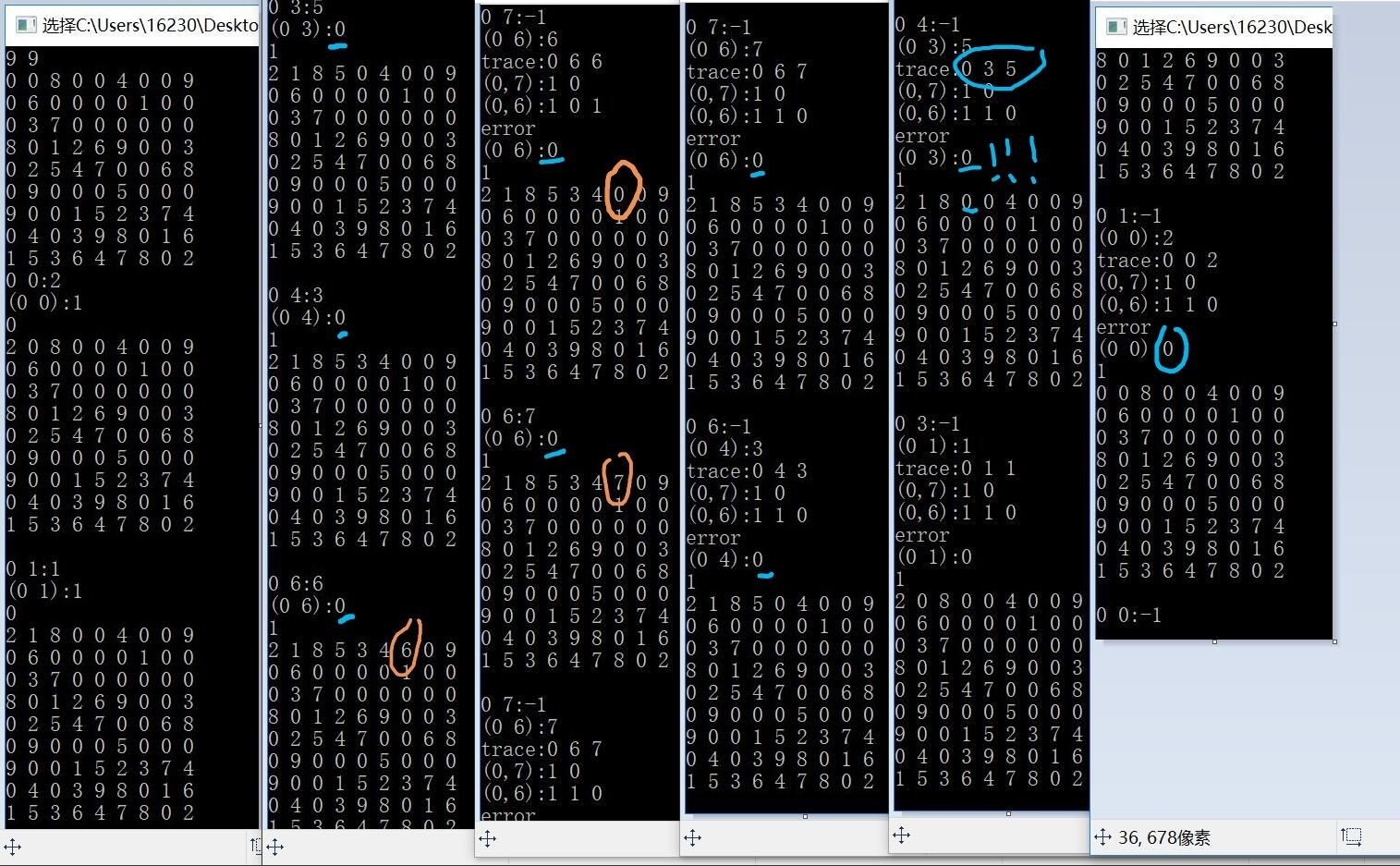
新思路就比较简单,将所有候选个数为1的格子填满,边填边更新格子状态,并将新产生的候选个数为1的格子加入更新队列,直至填满整个表盘。
实现方法:将空格加入队列,每次弹出一个空格填入,产生新的加入。这种方法仅适用于简单无多解的低宫格。保留开始时设计的count()函数、init()函数。可测试通过题目所给的两个表盘,和其他稍微简单的唯一解不用试探的九宫格。
性能改进
1.从九宫格更改部分参数,可延申至需要考虑宫的四六八宫格,参数的改变体现在init()函数中。并且当对应参数置0,并跳过扫描宫的步骤,可实现三五七仅需考虑行列影响的程序,综合后可实现三到九的简单数独解法。其中X为输入的宫数,N,M为对应宫格下,扫描行列宫时需要扫描的范围变化。
void init(int x,int y,int vv,int X) //扫描方圆几里,更新参数 ,注意vv不可为0
{
int N;
int M;
switch(X)
{
case 9:
{
N=3;M=3;break;
}
case 8:
{
N=4;M=2;break;
}
case 6:
{
N=2;M=3;break;
}
case 4:
{
N=2;M=2;break;
}
case 3:case 5:case 7:
{
N=0;M=0;break;
}
}
for(int i=0;i<X;i++)
{
no[X*x+i].v[vv]=1; //改为不可候选状态(1)
no[X*i+y].v[vv]=1;
}
for(int i=0;i<X;i++)
{
count(i,y,X);
count(x,i,X);
}
if(M==0&&N==0) return ;
int xs,ys;
xs=x/N*N;
ys=y/M*M;
for(int i=xs;i<xs+N;i++)
{
for(int j=ys;j<ys+M;j++)
{
no[X*i+j].v[vv]=1;
}
}
for(int i=xs;i<xs+N;i++)
{
for(int j=ys;j<ys+M;j++)
{
count(i,j,X);
}
}
}
2.对于多次处理表盘,另设reset()函数,每次输入表盘前将grid[][]表盘和81个node清空。并将除输入、初始化表盘、输出部分外的代码用fun()封装,使代码传入X、M、N参数更方便。
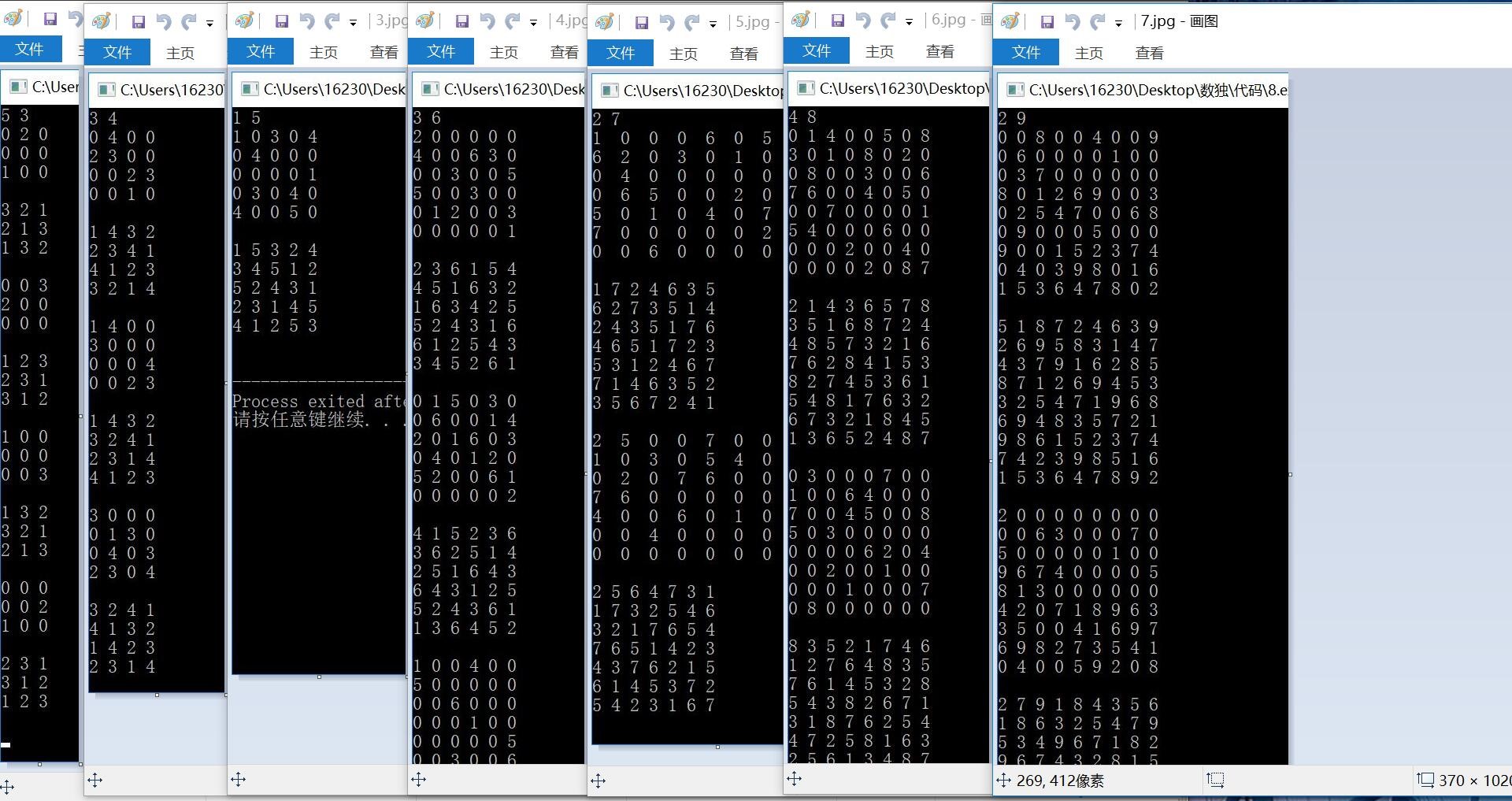
3.改为带有文件操作的程序:加入fopen()、fclose()和fscanf()、fprintf()函数
4.为处理命令行指令,添加代码
FILE* fp;
fp = NULL;
FILE* fq;
fq = NULL;
string inputname; //命令行输入处理
string outputname;
string a, b, c, d;
a = "-m";
b = "-n";
c = "-i";
d = "-o";
for (int i = 1; i < argc; i++)
{
if (argv[i] == c)
{
fp = fopen(argv[++i], "r"); //以文本方式打开文件。
if (fp == NULL) //打开文件出错
{
cout << "Input not found.\n" << endl;
return 0;
}
continue;
}
if (argv[i] == d)
{
fq = fopen(argv[++i], "w"); //以文本方式打开文件。
if (fq == NULL) //打开文件出错
{
cout << "Output not found.\n" << endl;
return 0;
}
continue;
}
if (argv[i] == a)
{
X = argv[++i][0] - '0';
continue;
}
if (argv[i] == b)
{
re = argv[++i][0] - '0';
continue;
}
}
该部分代码的单元测试:
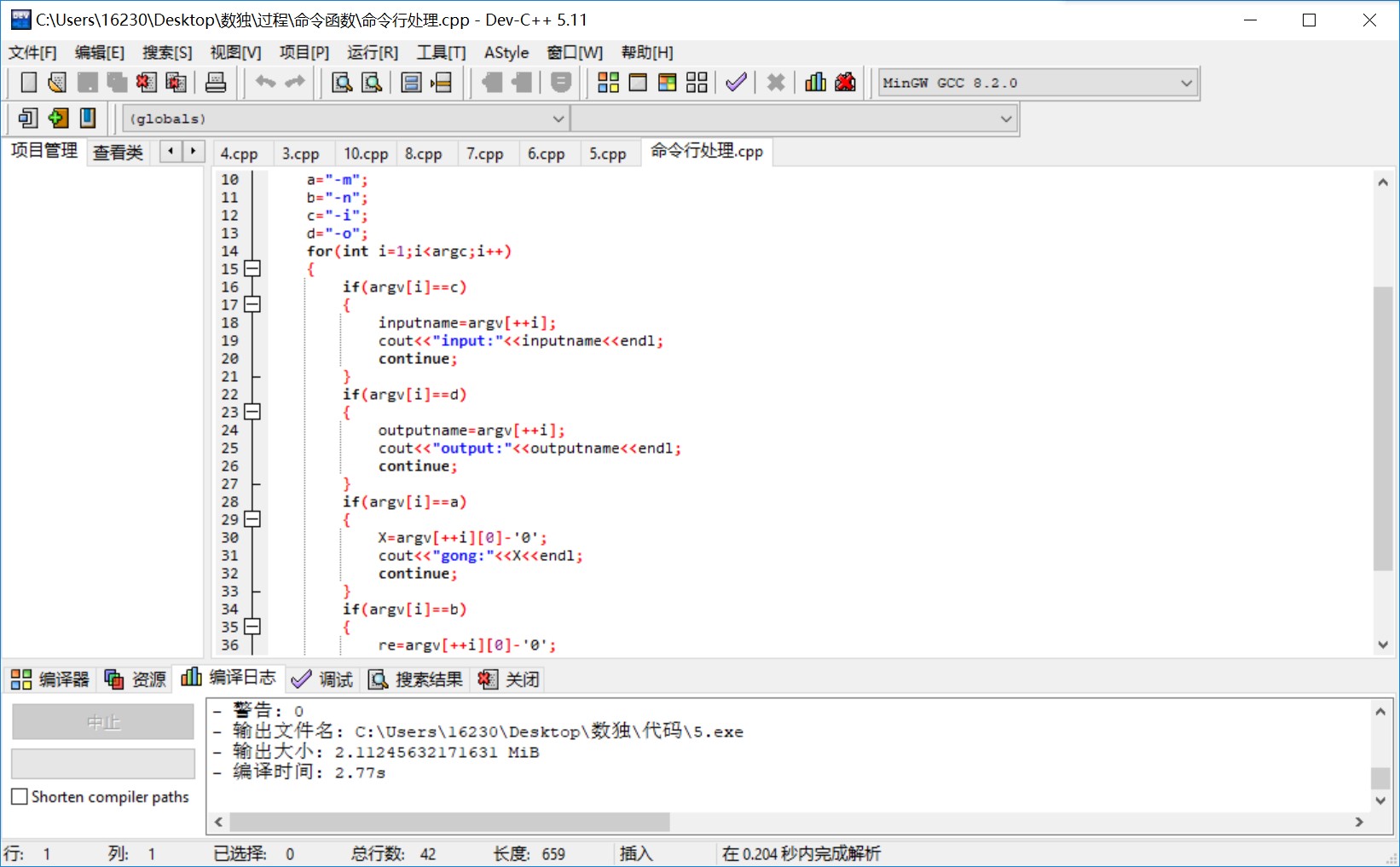
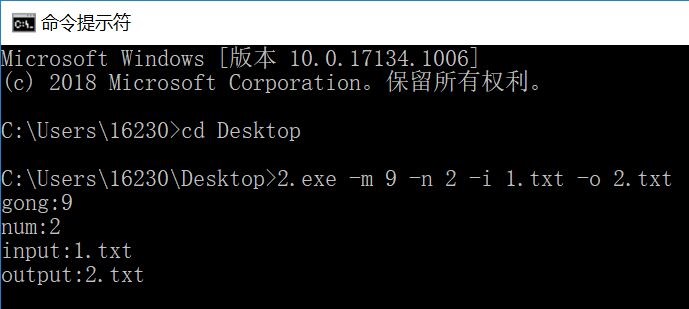
基本完成代码
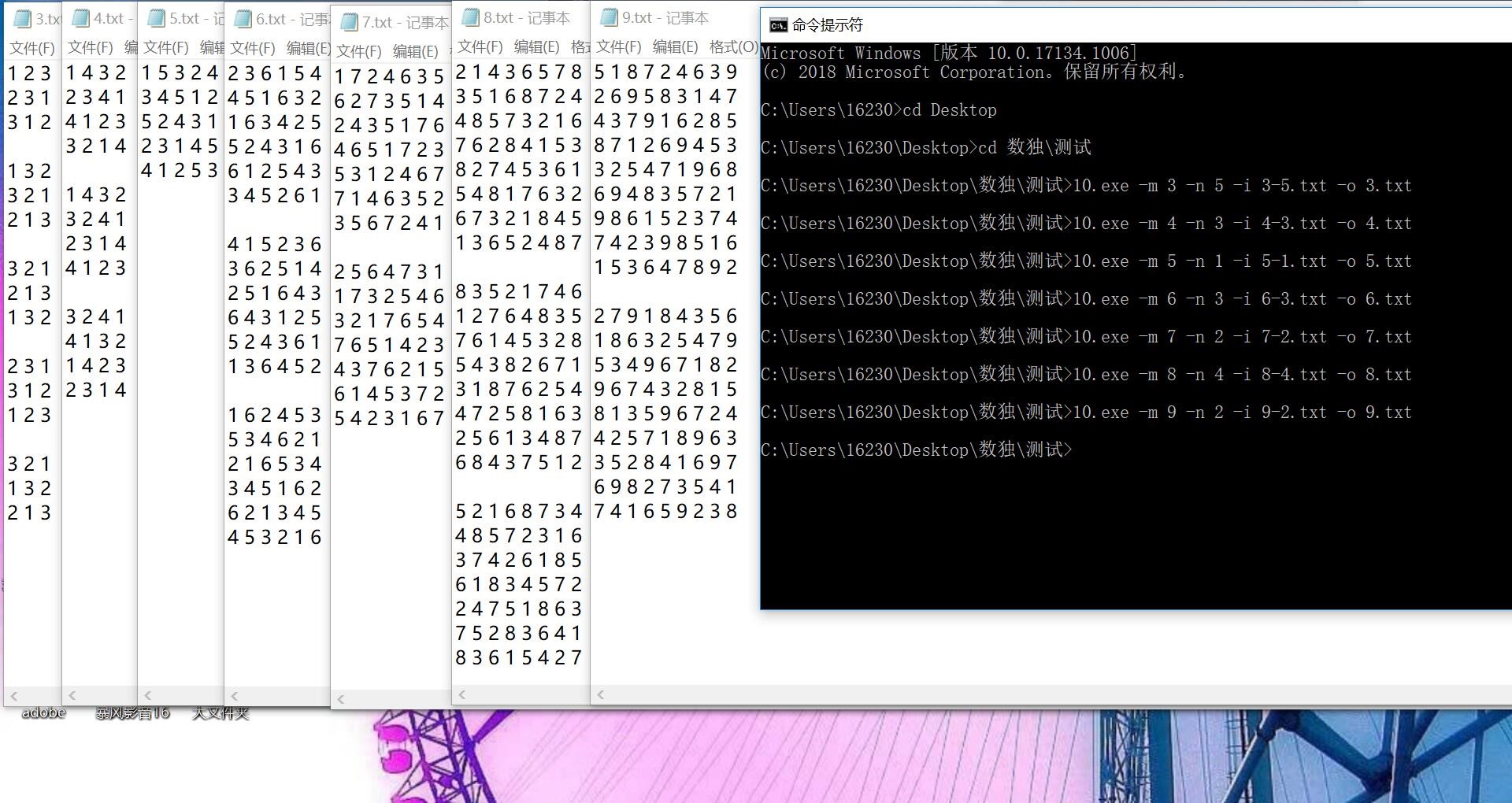
异常情况:
七宫格以上容易遇到虽是唯一解,但所有仅有一个候选数字的空格填满后,剩余格子需要尝试填入后发现问题,稍加修改即可得到正确答案的情况,代码暂时不能处理。即复杂的唯一解问题和多解问题暂时无法解决。
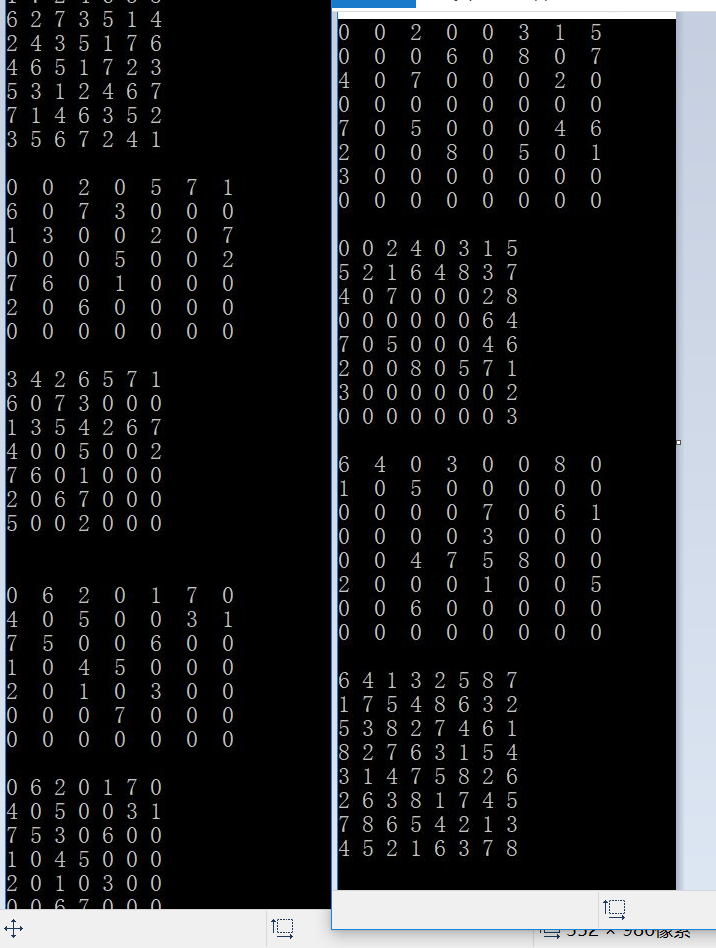
解决异常:在原代码的基础上,加入dfs深搜操作,将init()扫描函数稍加修改,变成可检测填入数字是否满足条件的判断函数check(),即扫描行、列、宫,若填入数字和已有数字相同,则返回0(即需要回溯),不重复则返回1(dfs可向下继续),加了dfs的代码,采用回溯法解决需要试探求解的复杂数独,即可以解决3-9宫格唯一解数独问题。
Code Quality Analysis检查结果
开始遇到状况有三个警告,并在生成可执行程序时,产生问题
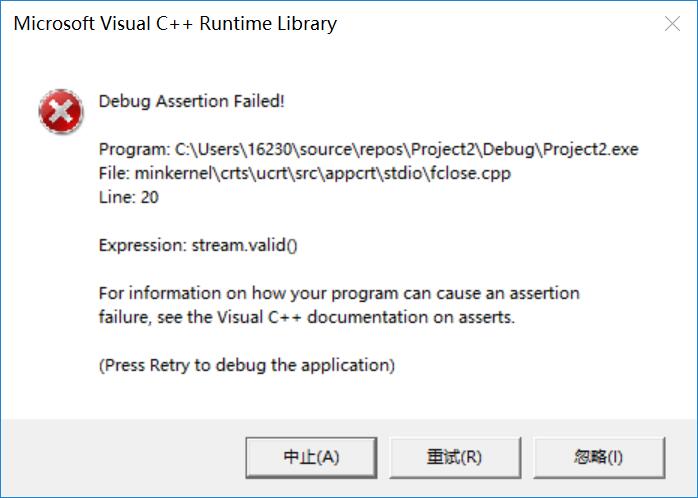
查资料后解决:文件指针没有初始化fp=NULL,并作相应的错误处理
fp = fopen(argv[++i], "r"); //以文本方式打开文件。
if (fp == NULL) //打开文件出错
{
cout << "Input not found.\n" << endl;
return 0; //直接返回
}
得到生成正确的解决方案
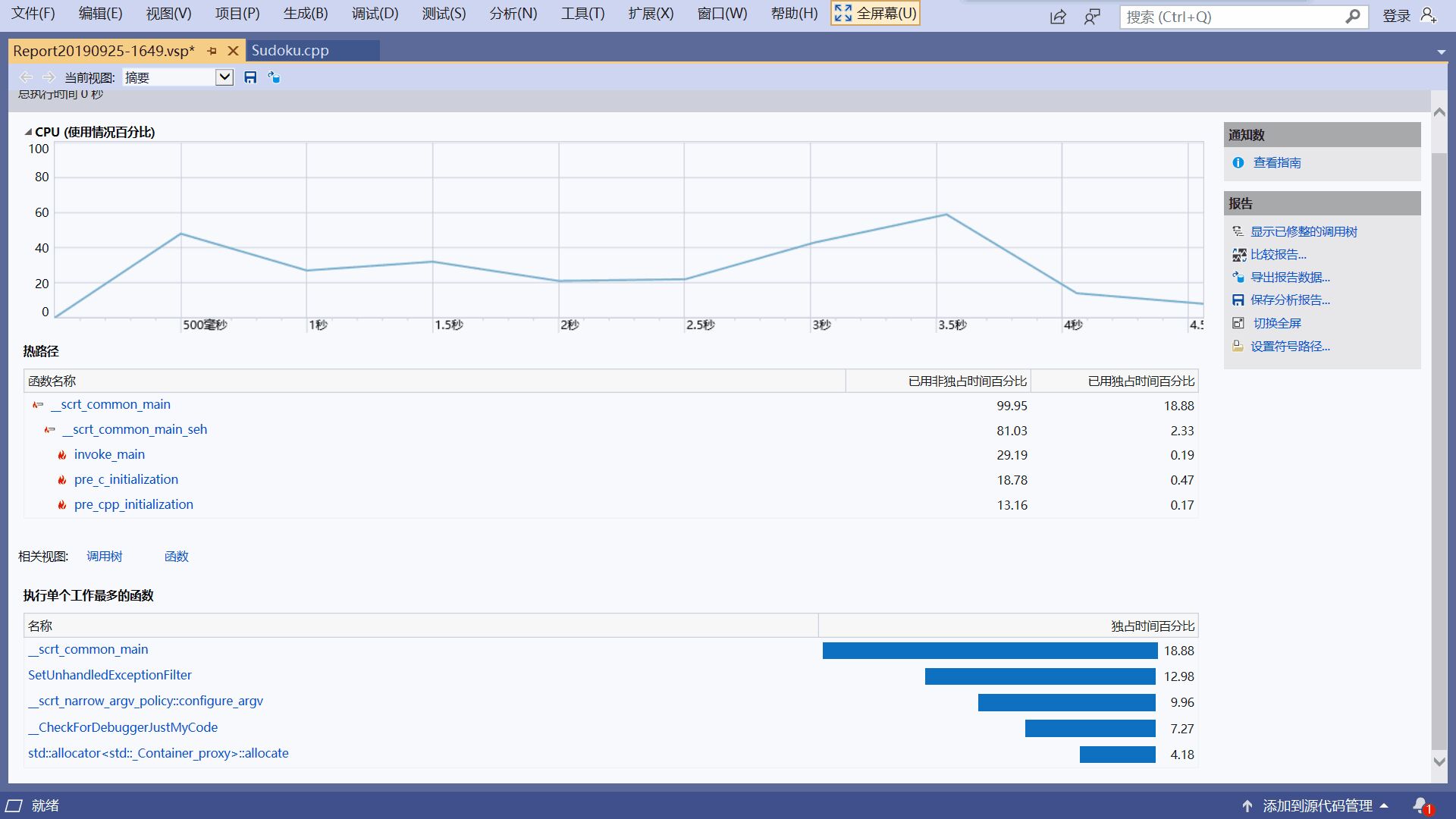
Studio Profiling Tools分析结果
心得体会
一次软工作业下来,一路上遇到很多问题,都需要自己逐一解决克服,在写作业的过程中需要学习的新东西很多, 收获不小,
从github的创建使用,新软件visual studio的安装和熟悉,预编译头文件的加入,性能分析工具的体验,让我体会到了代码之外,还有更广阔的天空。