最近再看支持向量机的时候，推公式时用到对偶问题。从而引出KKT条件,参考http://blog.csdn.net/johnnyconstantine/article/details/46335763
KKT条件是解决最优化问题的时候用到的一种方法。这里的最优化问题通常是指对于给定的某一函数，求其在指定作用域上的全局最小值。提到KKT条件一般回附带的提一下拉格朗日乘子，两者均是求解最优化问题的方法，不同之处在于
(1)无约束条件
这是简单的情况，解决方法通常是函数对变量求导，令导数等于零的点可能是极值点。将结果带回原函数进行验证
(2)等式约束条件
设目标函数为f(x),约束条件为hk(x),如下:
则解决方法拉格朗日函数F(x),
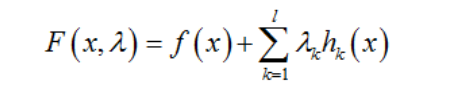
其中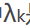
是各个约束条件的待定系数。
然后解变量的偏导方程：
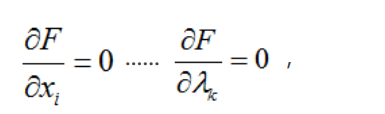
如果有l个约束条件，就应该有l+1个方程。求出的方程组的解就可能是最优化值（高等数学中提到的极值），将结果带回原方程验证就可得到解。
（3）不等式约束条件
设目标函数f(x),不等式约束为g(x) 等式约束为h(x) 此时问题的描述为:
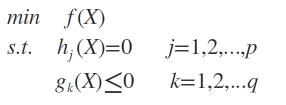
则我们定义不等式约束下的拉格朗日函数L
其中f(x)是原目标函数，hj(x)是第j个等式约束条件，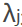
是对应的约束系数约束条件，gk是不等式约束，uk是对应的约束系数
此时若要求解上述优化问题，必须满足下述优化条件
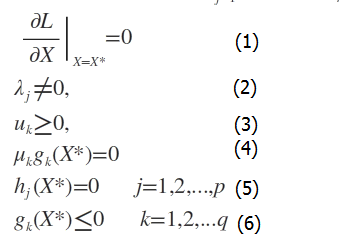
这些求解条件就是KKT条件。(1)是对拉格朗日函数取极值时候带来的一个必要条件，(2)是拉格朗日系数约束（同等式情况），(3)是不等式约束情况，(4)是互补松弛条件，(5)、(6)是原约束条件。
对于一般的任意问题而言，KKT条件是使一组解成为最优解的必要条件，当原问题是凸问题的时候，KKT条件也是充分条件。