数据结构和算法总结（二）：排序

前言

复习各种排序算法，并记录下。

正文

1.冒泡排序

冒泡可以说是最简单的排序算法，它的排序过程就是每次遍历数组将最大的那个数往前顶，就好像气泡上浮一样。

过程可以参考如下图

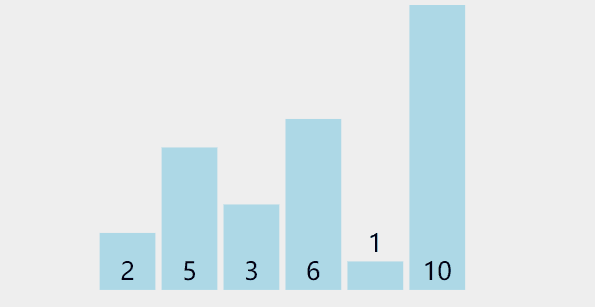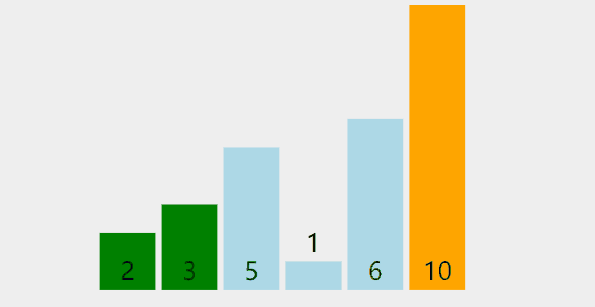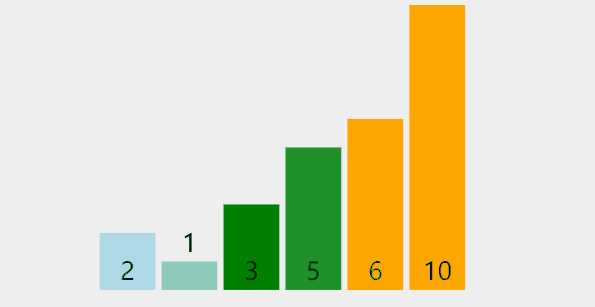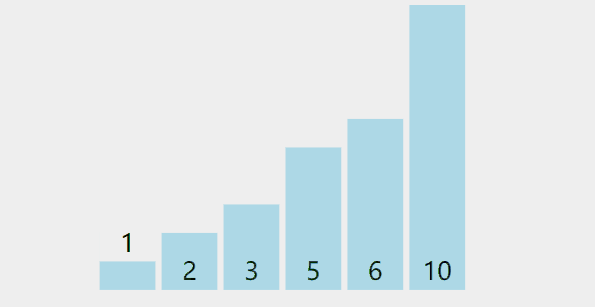
参考代码

void bubbleSort(vector<int>& num)
{
    for(int i = num.size()- 1;i > 0;i--)
    {
       for(int j = 1;j <= i;j++)
       {
           if(num[j] < num[j-1])
            swap(num[j],num[j-1]);
       }
    }
}

复杂度分析

冒泡的最坏情况下的时间复杂度为：O（n²），平均复杂度：O（n²） 。

优化

我们可以稍微优化下冒泡排序，增加一个标识来确定一个数组是否有序，如果是那么可以提前终止排序，参考代码如下

//提前终止的冒泡排序
bool PreStopBubble(vector<int>& num,const int n)
{
   bool isSwapped = false;
   for(int i = 1;i < n;i++)
   {
       if(num[i - 1] > num[i])
       {
           isSwapped = true;
           cout << "Swapped!" << endl;
           swap(num[i - 1],num[i]);
       }
   }
   return isSwapped;
}

void PreStopBubbleSort(vector<int>&num)
{
  for(int i = num.size();i > 0 && PreStopBubble(num,i);i--); 
  //如果某一次冒泡过程未发生交换，那么说明数组已经有序，所以提前终止
}

这种情形下，冒泡排序的最好复杂度可以达到O（n）。

2.选择排序

选择排序和冒泡排序的思路类似，都是找到最大（或者最小）的数，只不过选择排序需要额外的空间来存储一次遍历过程中最大（或者最小）的数字和它的位置，然后将它与首位（或者末位）交换。

过程可以参考如下图

注：图中的选择排序每次是选择的最小值，参考代码每次是选取最大值。

参考代码

void SelectionSort(vector<int>& num)
{
    for(int i = num.size();i > 0 ;i--)
    {
        int tmp = num[0],index = 0;
        for(int j = 1;j < i;j++)
        {
           if(num[j] > tmp)
           {
               tmp = num[j];
               index = j;
           }
        }
        swap(num[index],num[i - 1]);
    }
}

复杂度分析

选择排序的最坏情况下的时间复杂度为：O（n²），平均复杂度：O（n²） 。但是往往选择排序效率优于冒泡排序（如果不是提前终止的冒泡），因为每一次遍历选择排序只需要发生一次交换，而冒泡排序可能发生了多次交换，然而，这是选择排序牺牲了额外空间来存储最值得来的。

3.计数排序

计数排序，也叫桶排序。这种排序方法适合已知一定范围内的数字排序，每一个数字都有一个对应的桶，一次遍历将数组的数字放入到对应的桶中进行统计，然后遍历每个桶将其输出即可。

过程可以参考如下图

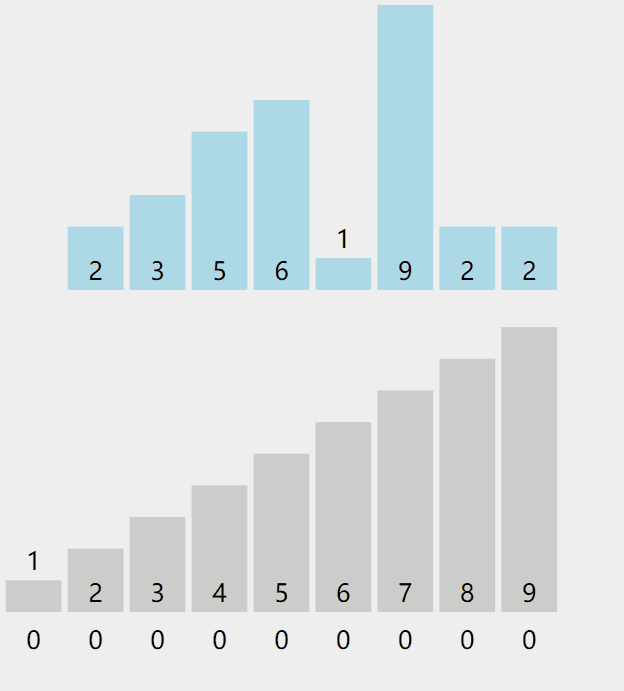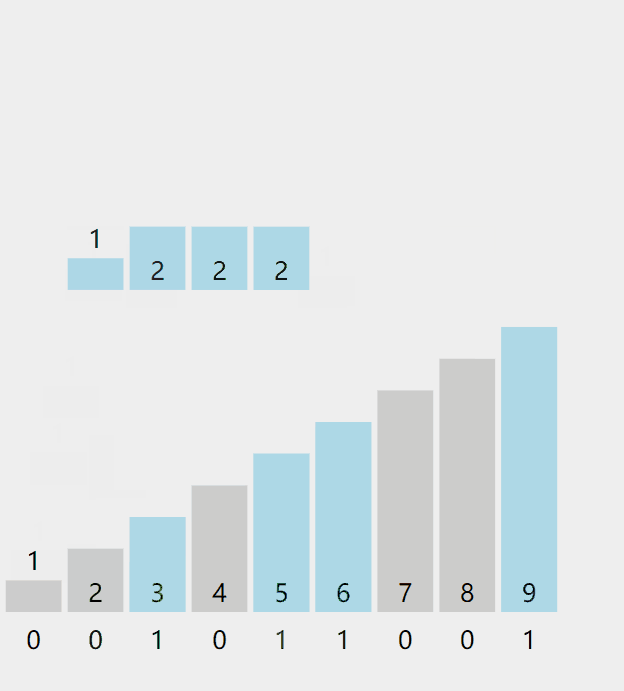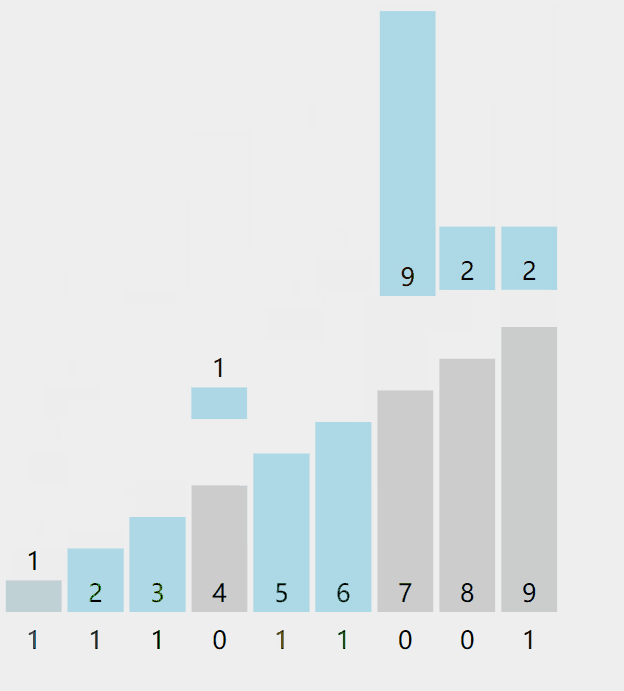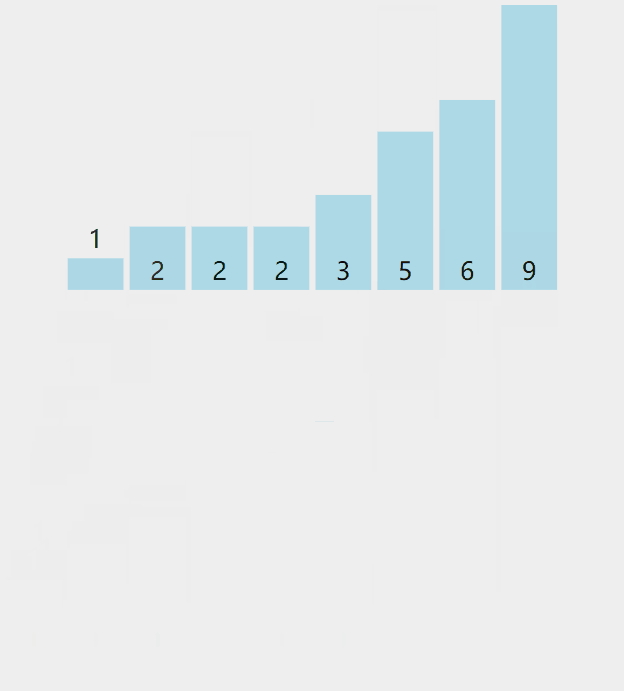
参考代码

void CountSort(vector<int>& num,const int maxnum)
{
   vector<int> countBox(maxnum + 1,0);
   for(int i =0;i < num.size();i++)
   {
       countBox[num[i]]++;
   }
   int j = 0;
   for(int i = 0;i < num.size();i++)
   {
      if(countBox[j]-- > 0)
        num[i] = j;
      else
      {
         j++;i--;
      }
   }
}

复杂度分析

计数排序的平均时间复杂度为：O（n）。但是它的空间复杂度很差。这是一种牺牲空间换取时间的排序算法。

4.归并排序

有序数组的合并

首先，我们要知道如何将两个有序数组合并。方法很简单，从头开始比较两个数组的数字，用一个额外的数组tmp存储一次比较时的较小数字，然后较小者所在数组的索引向后+1继续和之前另一个数组的较大者比较。如果其中一个数组遍历到末尾，那么把另一个数组的剩余元素依次添加到tmp数组末尾即可，这样tmp就是一个合并后的有序数组。

分治

而对于一个无序数组，我们可以将它划分为两个无序子数组，子数组又可以不停划分，直到当一个子数组只有一个数时，这时这个子数组肯定是有序的，那么我们就可以将一个个有序子数组合并成更大的有序子数组，直到最终合并成一个有序数组，这就是归并排序的思想。

排序过程可以参考如下图

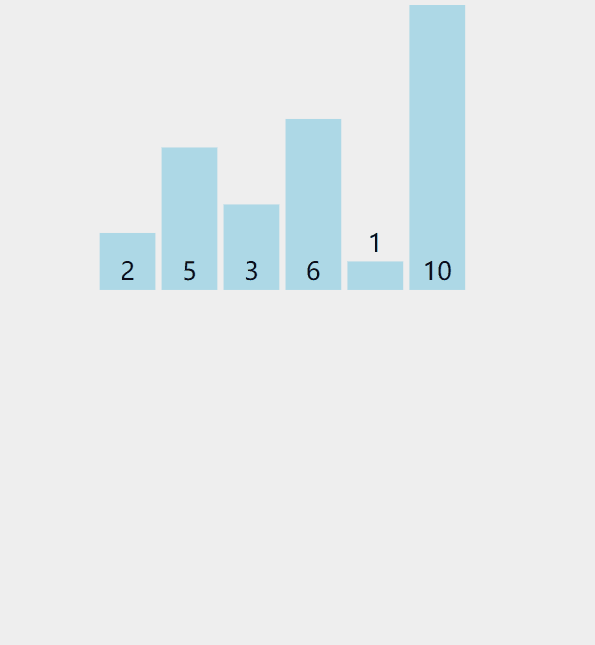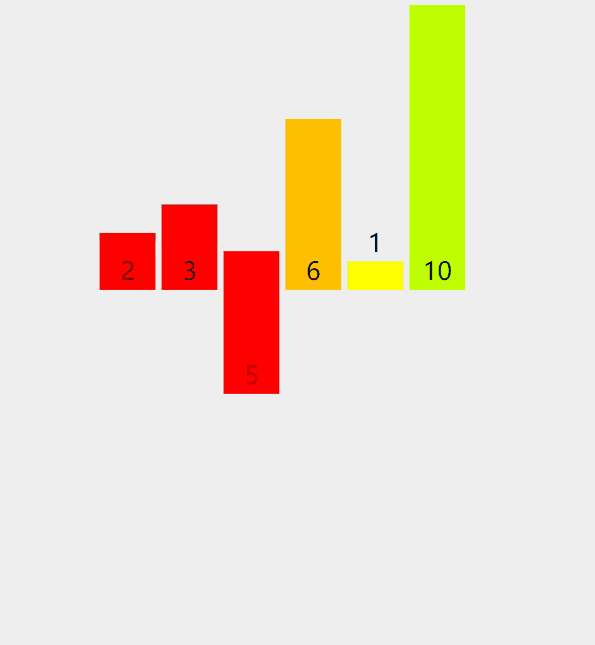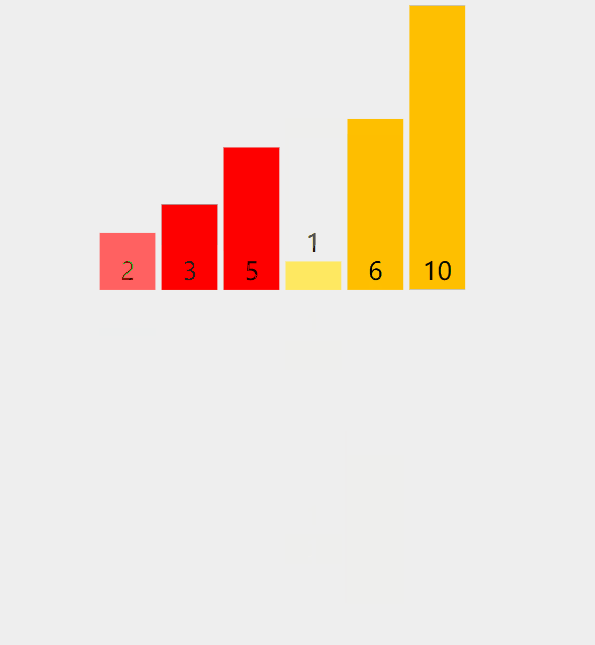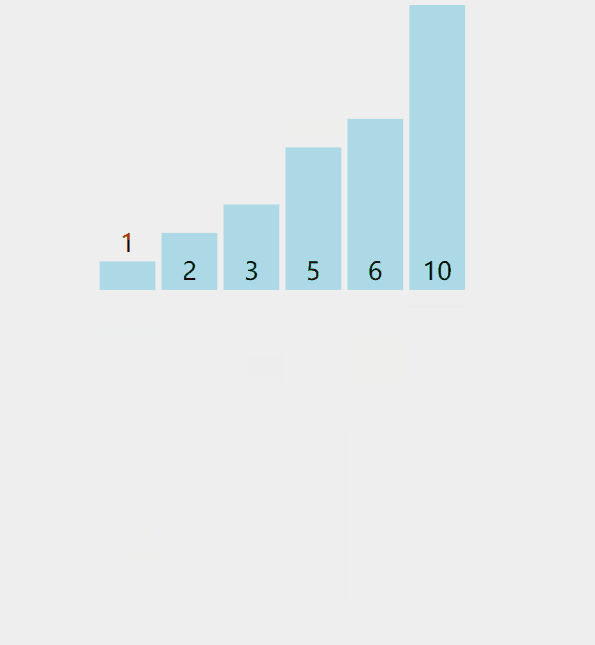
参考代码

void MergeArray(vector<int>& num,int left,int right,int mid,vector<int>& tmp)
{ //合并两个有序子数组
    int l = left,lm = mid;
    int mr = mid + 1,r = right;
    int k = 0;
    while(l <= lm && mr <= r)
    {
        if(num[l] < num[mr])
            tmp[k++] = num[l++];
        else
            tmp[k++] = num[mr++];
    }
    while(l <= lm) tmp[k++] = num[l++];
    while(mr <= r) tmp[k++] = num[mr++];
    for(int i = 0;i < k;i++)
    {
        num[left + i] = tmp[i];
    }
}

void MergeSort(vector<int>& num,int left,int right,vector<int>& tmp) 
{
   if(left >= right)
    return;
   int mid = (left + right)/2;
  //递归+分治
   MergeSort(num,left,mid,tmp);  
   MergeSort(num,mid + 1,right,tmp);
   MergeArray(num,left,right,mid,tmp);
}

void MergeSort_begin(vector<int>& num) //归并排序入口
{
    if(num.empty())
        return ;
    vector<int> tmp(num.size());
    MergeSort(num,0,num.size() - 1,tmp);
}

复杂度分析

归并排序的最坏时间复杂度为：O（nlogn），平均复杂度为：O（nlogn）。

5.快速排序

快速排序的思想从本质来说与归并排序类似，也是分治。只不过快速排序是在数组中选定了一个轴点，比轴点小的数字划分到左边，比轴点大的划分到右边，这样一个数组就被划分成了两部分，然后在这两部分基础上继续选择一个轴点划分，如此直到无法划分为止。

排序过程可以参考如下图

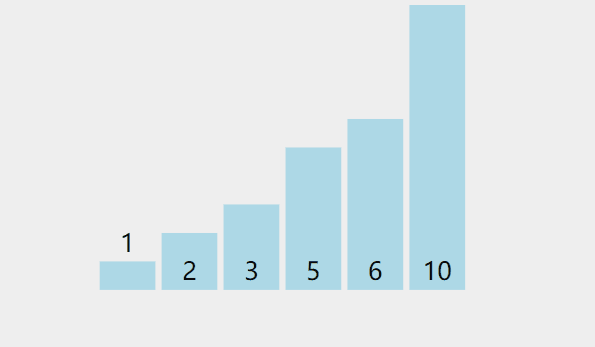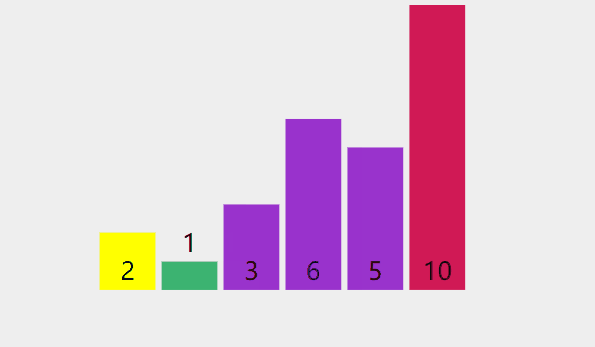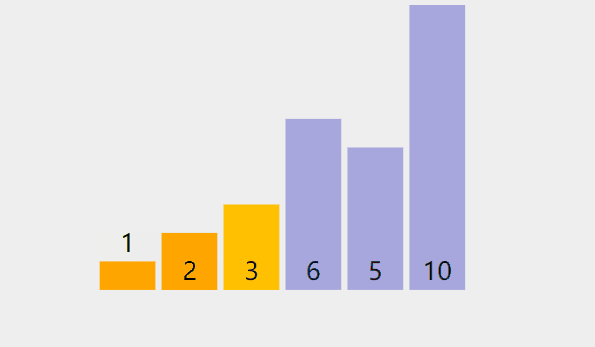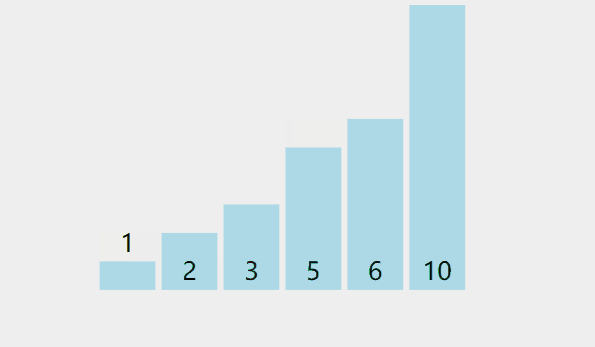
参考代码

注：这里是选取每个数组最左边的数字为轴点。

int qs_partition(vector<int>& num,int left,int right)
{
  int pivot = num[left];
  int l = left,r =right;
  while(l < r)
  {
      while(l < r && num[r] >= pivot) r--;
      if(l < r)
        num[l++] = num[r];
      while(l < r && num[l] < pivot) l++;
      if(l < r)
        num[r--] = num[l];
  }
  num[l] = pivot;
  return l;
}

void quickSort(vector<int>& num,int left,int right)
{
  if(left > right)
    return;
  int k = qs_partition(num,left,right);
  quickSort(num,left,k - 1);
  quickSort(num,k + 1,right);
}

上述的为递归的快速排序，如果数据量非常大可能会导致栈内存爆掉，所以可以用一个栈来实现非递归的快速排序。

非递归的快速排序参考代码

int qs_partition(vector<int>& num,int left,int right)
{
  int pivot = num[left];
  int l = left,r =right;
  while(l < r)
  {
      while(l < r && num[r] >= pivot) r--;
      if(l < r)
        num[l++] = num[r];
      while(l < r && num[l] < pivot) l++;
      if(l < r)
        num[r--] = num[l];
  }
  num[l] = pivot;
  return l;
}

void stack_quickSort(vector<int>& num)
{
    int left = 0,right = num.size() - 1;
    if(left > right)
        return;
    stack<int> stk;
    int l,r;
    stk.push(right);
    stk.push(left);
    while(!stk.empty())
    {
        l = stk.top();stk.pop();
        r = stk.top();stk.pop();
        if(l < r)
        {
            int k = qs_partition(num,l,r);
            stk.push(k - 1);stk.push(l);
            stk.push(r);stk.push(k + 1);
        }
    }
}

复杂度分析　　

快速排序的最坏时间复杂度为：O（n²），即轴点的左侧或者右侧没有数字。最好的情况是左右两侧数字大致相同，平均复杂度为：O（nlogn）。

补充

快速排序的轴点选择对于该排序算法的效率有很大的影响，最普通的选取最左或者最右的数字作为轴点的方法其实不太稳定，常用的选取轴点的方法是随机取值或者三值取中。

三值取中：顾名思义，在最左、最右、中间三个位置选取三个数字，然后在三个数字中选取值居于中间的那个数字作为轴点。

参考资料

《数据结构、算法与应用——C++描述》   作者：【美】 萨特吉·萨尼       机械工业出版社

  Visualgo算法可视化网站