信息安全－5：RSA算法详解(已编程实现)[原创]

 转发注明出处:http://www.cnblogs.com/0zcl/p/6120389.html

背景介绍

1976年以前，所有的加密方法都是同一种模式：

　　（1）甲方选择某一种加密规则，对信息进行加密；

　　（2）乙方使用同一种规则，对信息进行解密。

由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-key algorithm）。

这种加密模式有一个最大弱点：甲方必须把加密规则告诉乙方，否则无法解密。保存和传递密钥，就成了最头疼的问题。

1976年，两位美国计算机学家Whitfield Diffie 和 Martin Hellman，提出了一种崭新构思，可以在不直接传递密钥的情况下，完成解密。这被称为"Diffie-Hellman密钥交换算法"。这个算法启发了其他科学家。人们认识到，加密和解密可以使用不同的规则，只要这两种规则之间存在某种对应关系即可，这样就避免了直接传递密钥。

这种新的加密模式被称为"非对称加密算法"。

　　（1）乙方生成两把密钥（公钥和私钥）。公钥是公开的，任何人都可以获得，私钥则是保密的。

　　（2）甲方获取乙方的公钥，然后用它对信息加密。

　　（3）乙方得到加密后的信息，用私钥解密。

如果公钥加密的信息只有私钥解得开，那么只要私钥不泄漏，通信就是安全的。

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。从那时直到现在，RSA算法一直是最广为使用的"非对称加密算法"。毫不夸张地说，只要有计算机网络的地方，就有RSA算法。

这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

RSA算法原理

RSA算法需要一些数学知识，不过别怂，不难的。我总结了一下，大概需要以下三部分的知识：

• 互质关系(这，很简单)
• 欧拉公式(难,我是直接记公式的)
• 模反元素(不难的)

接下来说下每个部分的内容：

1、互质关系:如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

2、先说下 欧拉函数:φ(n)为比n小但与n互素的正整数个数，称为n的欧拉函数。对任一素数p, 有φ(n)＝p-1，而对于两个不同的素数p和q，则对n=pq，可以证明φ(n)＝φ(pq)=(p-1)(q-1)=φ(p)*φ(q)

3、模反元素:如何求模反元素(逆元)，用辗转相除法，我在上一篇博客<信息安全－4:公钥密码体制之背包算法[原创]>有说，看了一定会懂的！

上面3点一定要GET，不然不用往下看了~~

RSA算法的过程

RSA算法可归纳如下:

1. 选择两个素数p和q，计算n=p*q，φ(n)=(p-1)(q-1),选择整数e,使gcd(φ(n), e)=1,1<e<φ(n),计算逆元d=e^-1modφ(n),于是得到公钥KU＝{e, n},私钥＝{d, n},而把p和q丢弃(PS:gcd(φ(n), e)=1 表示最大公约数为1,下面编程有用到~)。
2. 加密(用公钥KU):明文M<n, 密文:C=m^e mod n
3. 解密(用私钥KR):密文:C, 明文:M=C^d mod n

上面过程很重要!!! 刚开始看会有点懵逼，看下面的例子，一定会懂!

我们通过一个例子，来理解RSA算法。假设Alice想发送明文9726给Bob，这之间的过程是怎样的？又是怎样生成公钥和私钥呢？

(1)Bob生成密钥 

Bob选择两个互异素数p=101和q=113，计算:n=pq=101*113=11413, φ(n)=(p-1)(q-1)=100*112=11200

由于加密密钥e必须与φ(n)没有公因子，假设Bob随机选择了e=3533，则用辗转相除法可求得: d=e^-1=3533^-1 mod 11200=6597

于是Bob公布他的公钥KU={3533, 11413}, 将私钥KR={6597, 11413}保密。

(2)Alice加密信息

由于Bob的公钥是公开的，任何人都可得到，因此Alice使用Bob的公钥来加密即将发送给Bob的明文信息。

Alice计算: 9726³⁵³³ mod 11413=5761, 然后在一个信道上发送密文5761.

(3)Bob解密密文

当Bob接收到密文5761时，他用他的私钥进行解密。

Bob计算: 5761⁶⁵⁹⁷ mod 11413=9726, 这样Bob就得到Alice发给他的明文信息了！！！

RSA算法编程实现

 

流程图

我画的流程图网址: https://www.processon.com/diagraming/583fb2c0e4b0d0d77bcfa514

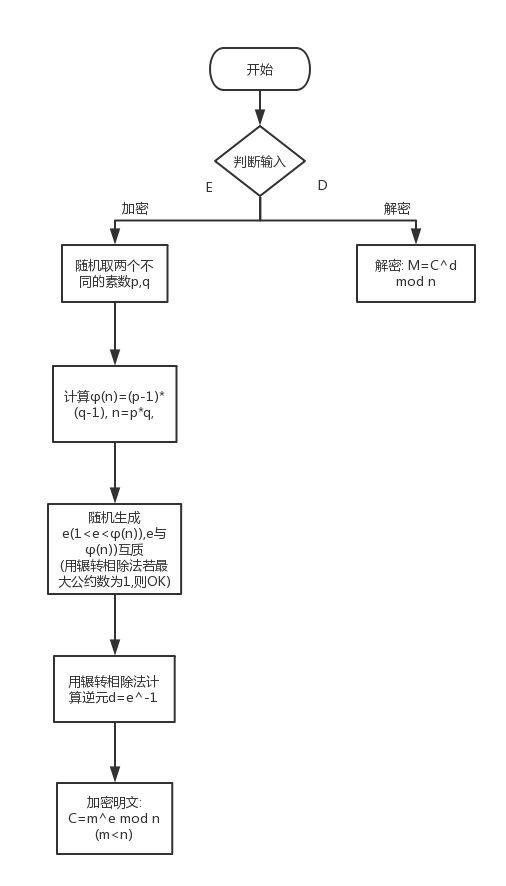
ReadMe:

1. 运行环境为python3.4   Windows8.1, 程序代码用Python语言写的
2. 质数P，Q是我自己给出的，当然也可以随机生成
3. 运行时，必须先加密再解密，因为先加密才有逆元给解密模块进行运算
4. 运行时有一些测试打印出来，为了方便了解程序运行过程，我这里就没有去除。

源代码

#RSA加密算法

import random
# p,q是两个不同的素数n=pq,按理说应该随机产生，这里我用p=101,q=103为例

P = 101
Q = 113
N = P * Q
global _E  # 把逆元定义为全局变量，才能在解密模块调用
_E = 0     #初始为0

#欧拉公式:如果n是质数，则 φ(n)=n-1 。因为质数与小于它的每一个数，都构成互质关系
F = (P-1) * (Q-1)


#求最大公约数，若最大公约数是1，且m,n>1,m与n不等，则说明m,n互质
def comm_div(m, n):      #m>n
    temp = m % n
    while(temp != 0):
        m = n
        n = temp
        temp = m % n
    if n == 1:         #说明互质，返回True
        return True


# 在1-9999之间随机选择一个整数e，条件是1< e < F，且e与F 互质
# 互质即说明e,F的公因子有且仅有1
def e_product():
    while True:
        rand = random.randrange(2, F)
        if comm_div(F, rand):
            e = rand
            return e


#用辗转相除法求质数e关于欧拉公式F的逆元
def _e_product(e, F):
    a_list = []
    m = F
    n = e
    temp = m % n

    while (temp != 0):
        a = (m - temp) / n
        a_list.append(a)
        m = n
        n = temp
        temp = m % n
    print("a_list:", a_list)
    a_list.reverse()    #逆序
    print("a_list_reverse:", a_list)
    b_list = []
    b_list.append(1)
    b_list.append(a_list[0])
    print("(最初插入的两个1及a_list[0])b_list:", b_list)
    for i in range(len(a_list)-1):
        b = b_list[-1] * a_list[i+1] + b_list[-2]
        b_list.append(b)

    print("b_list", b_list)
    #a_list存放的是商数，如果商数个数是偶数 b_list[-1]即为所求逆元
    #若为奇数，F-b_list[-1]为所求的逆元
    if len(a_list) % 2 == 0:   #偶数
        return b_list[-1]
    else:
        return F - b_list[-1]


#传入明文(数字)和公钥，进行加密,返回密文
def core_encryption(clear_text, e, N):
    clear = clear_text
    for i in range(e-1):
        clear_text = clear_text  * clear
    cipher_text = clear_text % N
    return cipher_text


def encryption(clear_text):
    clear_text = int(clear_text)
    e = e_product()
    print("随机产生的e:%s" % e)
    global _E       #对全局变量进行重新赋值，需要global
    _E = _e_product(e, F)
    # print("逆元_e:", _E)
    # print("逆元类型:",type(_E))
    print("公钥KU:%d,%d
私钥KR:%d,%d" % (e,N, _E,N))
    cipher_text = core_encryption(clear_text,e,N)
    return cipher_text


#根据之前加密生成的私钥进行解密，所以必须先有加密才行的
def decryption(cipher_text, _e, N):
    cipher_text = int(cipher_text)
    cipher = cipher_text
    # print(_e)
    # print("逆元_e类型:",type(_e))
    for i in range(_e-1):
        cipher_text = cipher_text * cipher
    clear_text = cipher_text % N
    return clear_text


if __name__ == "__main__":
    while True:
        print("必须先加密后解密！".center(50, "-"))
        choice = input("Input E for encryption or D for decryption:")
        if choice == "E":
            clear_text = input("请输入明文(只允许数字):")
            if clear_text.strip().isalnum():
                print("加密成功！密文为:%d" % encryption(clear_text))
        if choice == "D":
            cipher_text = input("请输入密文:")
            if cipher_text.strip().isalnum():
                print("解密成功！明文为:%d" % decryption(cipher_text, _E, N))

问题

在测试时我遇到了下面这个问题

C:Python34python3.exe C:/Users/Administrator/PycharmProjects/xingxi/playfair/RSA.py
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:E
请输入明文(只允许数字):9726
随机产生的e:2147
a_list: [5.0, 4.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 2.0, 1.0, 1.0, 1.0]
a_list_reverse: [1.0, 1.0, 1.0, 2.0, 1.0, 1.0, 1.0, 1.0, 1.0, 1.0, 4.0, 5.0]
(最初插入的两个1及a_list[0])b_list: [1, 1.0]
b_list [1, 1.0, 2.0, 3.0, 8.0, 11.0, 19.0, 30.0, 49.0, 79.0, 128.0, 591.0, 3083.0]
公钥KU:2147,11413
私钥KR:3083,11413
加密成功！密文为:5200
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:D
请输入密文:5200
Traceback (most recent call last):
  File "C:/Users/Administrator/PycharmProjects/xingxi/playfair/RSA.py", line 116, in <module>
    print("解密成功！明文为:%d" % decryption(cipher_text, _E, N))
  File "C:/Users/Administrator/PycharmProjects/xingxi/playfair/RSA.py", line 99, in decryption
    for i in range(_e-1):
TypeError: 'float' object cannot be interpreted as an integer

Process finished with exit code 1

现在已经解决了，问题出在了下面第6行代码，rang()函数里面不能是float型，只需要int(_e-1)转型即可解决！

def decryption(cipher_text, _e, N):
    cipher_text = int(cipher_text)
    cipher = cipher_text
    # print(_e)
    # print("逆元_e类型:",type(_e))
    for i in range(_e-1):   
        cipher_text = cipher_text * cipher
    clear_text = cipher_text % N
    return clear_text

你可能会说，毛线，这么简单的坑你都跳(鄙视脸)。

好吧，这都怪我在这之前输出了一条测试print("_e:%d" % _e)，然后我运行时看到输出的是整型，就蒙比了，心想:明明是int型，怎么会爆错说float型！！！这大概就是所谓的被自己挖的坑坑到怀疑人生吧~~

 测试(为了方便我日后再来看，一些打印测试我没有去除)

C:Python34python3.exe C:/Users/Administrator/PycharmProjects/xingxi/playfair/RSA.py
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:E
请输入明文(只允许数字):9726
随机产生的e:4031
a_list: [2.0, 1.0, 3.0, 1.0, 1.0, 17.0, 2.0, 1.0, 3.0]
a_list_reverse: [3.0, 1.0, 2.0, 17.0, 1.0, 1.0, 3.0, 1.0, 2.0]
(最初插入的两个1及a_list[0])b_list: [1, 3.0]
b_list [1, 3.0, 4.0, 11.0, 191.0, 202.0, 393.0, 1381.0, 1774.0, 4929.0]
公钥KU:4031,11413
私钥KR:6271,11413
加密成功！密文为:325
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:D
请输入密文:325
解密成功！明文为:9726
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:E
请输入明文(只允许数字):25
随机产生的e:6403
a_list: [1.0, 1.0, 2.0, 1.0, 75.0, 2.0]
a_list_reverse: [2.0, 75.0, 1.0, 2.0, 1.0, 1.0]
(最初插入的两个1及a_list[0])b_list: [1, 2.0]
b_list [1, 2.0, 151.0, 153.0, 457.0, 610.0, 1067.0]
公钥KU:6403,11413
私钥KR:1067,11413
加密成功！密文为:10272
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:D
请输入密文:10272
解密成功！明文为:25
--------------------必须先加密后解密！---------------------
Input E for encryption or D for decryption:

注:RSA算法背景参考自http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html

    博客参考书籍:信息安全概论(凌捷  谢赞福   编著)

    接下来一个月信息安全方面可能最多会再写一篇博客, 重心会放在人工智能和操作系统!fight!