世界上最不缺的就是好题。
首先考虑暴搜。(还有什么题是从这东西推到正解的……)
首先单独一个换乘站明显没用,只用考虑一对对的换乘站。
那么有八种情况:(从题解偷图)
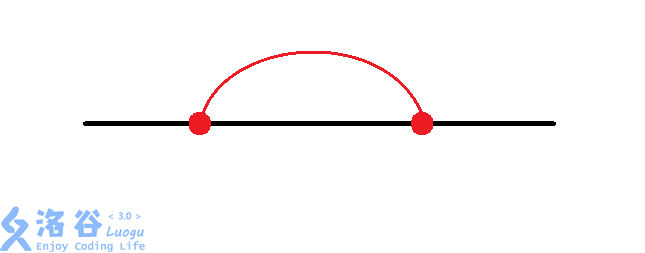
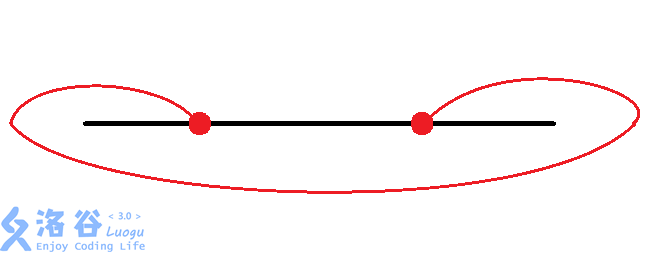
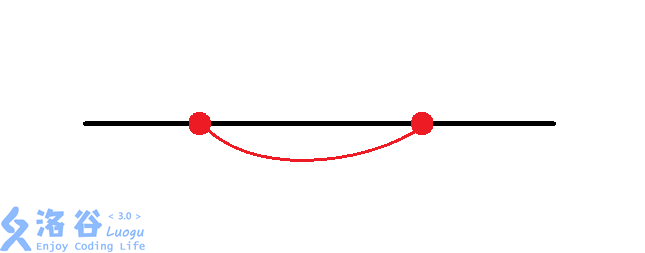
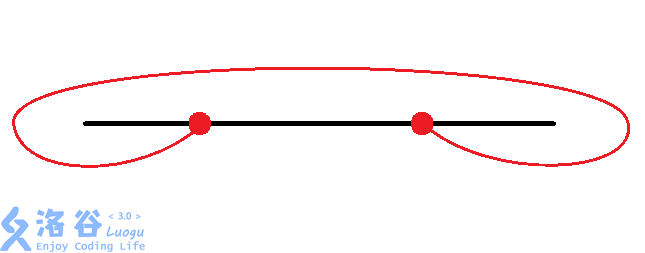
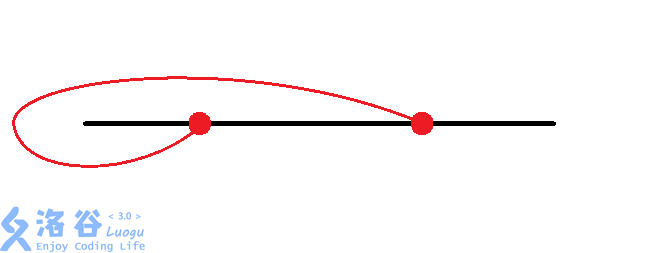
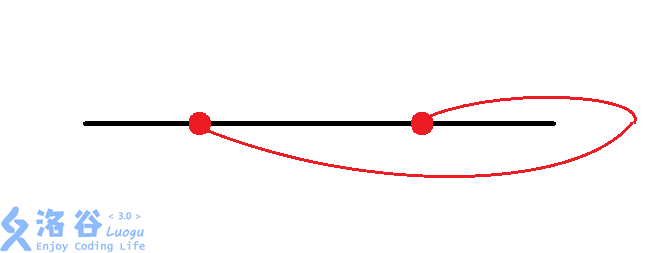
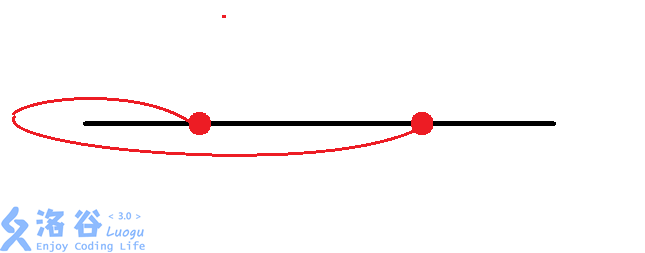
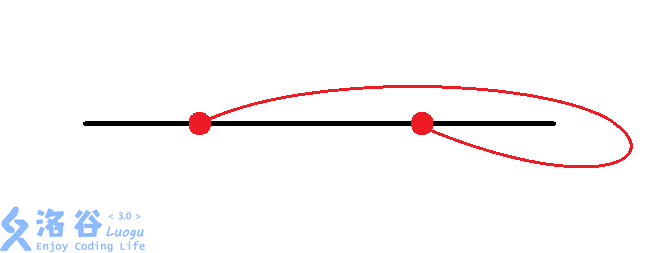
然后大力枚举每个换乘站的情况。同时判断交点。$O(n imes 8^{frac{n}{2}})$。
然后考虑这种情况:
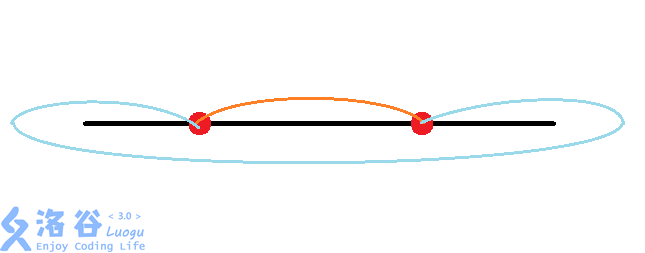
发现对于任意一条地铁线,要么与这两个都有交点,要么可以与这两个都没有交点。(其实会有与一个有两个交点,与另一个没有交点的情况。这时也可以把这条线换个方向,答案不会更差。思考思考为什么)
那么合法状态只剩四种:




再考虑这两个线路:
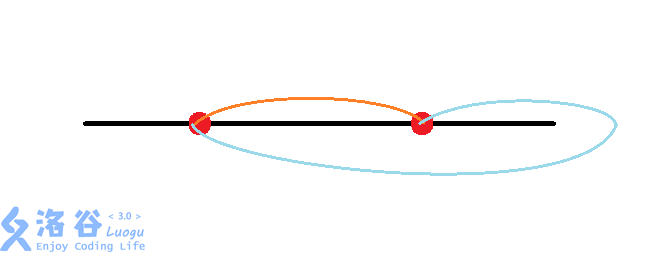
发现,虽然对于左端点在第一个红点右边的地铁线,这两种没有区别,但是对于左端点在第一个红点左边的地铁线,它们可能有区别。
不过由于我们搜索是按左端点从小到大搜的,所以可以贪心取目前这两条线最优的一条,不会影响后面的值。
最后每次合法状态只剩两个。$O(n imes 2^{frac{n}{2}})$。
此时合法状态不可能再减少了。考虑加速求交点个数。
发现对于左端点小于当前地铁线的左端点的地铁线,与这个地铁线有交点当且仅当右端点在一个区间(具体看代码)内。
那么可以用树状数组优化。每次给右端点打个标记,然后就变成了求区间和。
$O(2^{frac{n}{2}}log n)$。
p.s:要调用很多次树状数组,常数也不小,我就挂了,挂成 80 分。
然而加上个普及组剪枝就过了。$sum>ans$ 时 $return$。
(普及组搜索剪枝不会了……智商越来越低了)

#include<bits/stdc++.h> using namespace std; typedef long long ll; const int maxn=45; #define FOR(i,a,b) for(int i=(a);i<=(b);i++) #define ROF(i,a,b) for(int i=(a);i>=(b);i--) #define MEM(x,v) memset(x,v,sizeof(x)) inline int read(){ int x=0,f=0;char ch=getchar(); while(ch<'0' || ch>'9') f|=ch=='-',ch=getchar(); while(ch>='0' && ch<='9') x=x*10+ch-'0',ch=getchar(); return f?-x:x; } int t,n,m,tp[maxn],l[maxn],r[maxn],ans,sum,b[2][maxn]; inline void update(int id,int p,int v){ while(p<=n){ b[id][p]+=v; p+=p&-p; } } inline int query(int id,int p){ int s=0; while(p){ s+=b[id][p]; p-=p&-p; } return s; } inline int query(int id,int l,int r){return query(id,r)-query(id,l-1);} void dfs(int dep){ if(sum>ans) return; if(dep>m) return void(ans=sum); int t1=query(0,l[dep],r[dep]),t2=query(0,r[dep],n),t3=query(1,l[dep],r[dep]),t4=query(1,r[dep],n); update(0,r[dep],1); sum+=min(t1,t2+t3+t4); dfs(dep+1); sum-=min(t1,t2+t3+t4); update(0,r[dep],-1); update(1,r[dep],1); sum+=min(t3,t1+t2+t4); dfs(dep+1); sum-=min(t3,t1+t2+t4); update(1,r[dep],-1); } int main(){ t=read(); while(t--){ m=0;ans=1e9; n=read(); FOR(i,1,n) tp[i]=read(); FOR(i,1,n) FOR(j,i+1,n) if(tp[i]==tp[j]) l[++m]=i,r[m]=j; dfs(1); printf("%d ",ans); } }
