A - Adrien and Austin
(n) 为奇数时先手必胜;为偶数时,若 (kleq1) ,则后手必胜,否则先手必胜。注意特判 (n=0)。
代码:
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n,k;
scanf("%d%d",&n,&k);
if(n==0)
{
printf("Austin
");
return 0;
}
if(n%2==0&&k<=1)
printf("Austin
");
else
printf("Adrien
");
return 0;
}
I - Magic Potion
一开始想的是二分图匹配,先进行一趟最大匹配,求出 (ans)。然后把匹配的点标记掉,再求一趟最大匹配,结果为 (res)。最终结果为:(ans+min(k,res))。但一直 (WA) 在第 (7) 个点。因为,第一遍求最大匹配时,最大匹配并非是唯一的,所以导致第二遍求的时候,就不一定是最大值。
所以,改用最大流来求解。
建图如下:(同时考虑人数和药水数量的限制)

代码:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
const int inf=0x3f3f3f3f;
const int N=1100;
struct node
{
int to,val,rev;
};
vector<node>pic[N];
queue<int>que;
int layer[N],iter[N];
int V,n,m,k;
bool bfs()
{
for(int i=1;i<=V;i++) layer[i]=-1;
while(!que.empty()) que.pop();
que.push(1);
layer[1]=0;
while(!que.empty())
{
int now=que.front();
que.pop();
for(int i=0;i<pic[now].size();i++)
{
node tmp=pic[now][i];
if(layer[tmp.to]<0&&tmp.val>0)
{
layer[tmp.to]=layer[now]+1;
que.push(tmp.to);
if(tmp.to==V) return 1;
}
}
}
return 0;
}
int dfs(int v,int c)
{
if(v==V) return c;
for(int &i=iter[v];i<pic[v].size();i++)
{
node &tmp=pic[v][i];
if(layer[tmp.to]>layer[v]&&tmp.val>0)
{
int d=dfs(tmp.to,min(c,tmp.val));
if(d>0)
{
tmp.val-=d;
pic[tmp.to][tmp.rev].val+=d;
return d;
}
}
}
return 0;
}
int dinic()
{
int max_flow=0,f=0;
while(bfs())
{
for(int i=1;i<=V;i++) iter[i]=0;
while((f=dfs(1,inf))>0)
max_flow+=f;
}
return max_flow;
}
void addedge(int v,int u,int w)
{
pic[v].pb(node{u,w,pic[u].size()});
pic[u].pb(node{v,0,pic[v].size()-1});
}
int main()
{
int x,t;
scanf("%d%d%d",&n,&m,&k);
V=n+m+3;
for(int i=1;i<=n;i++)
{
scanf("%d",&t);
for(int j=1;j<=t;j++)
{
scanf("%d",&x);
addedge(i+2,x+2+n,2);
}
}
addedge(1,2,k);
for(int i=3;i<=n+2;i++)
{
addedge(2,i,1);
addedge(1,i,1);
}
for(int i=n+2+1;i<=2+n+m;i++) addedge(i,V,1);
printf("%d
",dinic());
return 0;
}
G - Pyramid
(n^3) 打表,找规律:
如下图:
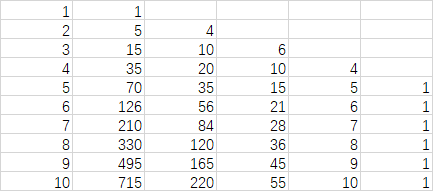
可以发现后面为等差数列,从后向前推。
所以:
一层一层拆开,利用公式:
(1^2+2^2+...+n^2=frac{n*(n+1)*(2*n+1)}{6})
和
(1^3+2^3+...+n^3=(1+2+3+...+n)^2)
最后可以化简出:
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1e9+7;
const ll inv2=500000004;
const ll inv6=166666668;
const ll inv12=83333334;
ll f1(ll x)
{
return x*(x-1)%mod*inv2%mod;
}
ll f2(ll x)
{
ll res=(x-1)*x%mod*(2*x-1)%mod*inv6%mod;
return res;
}
int main()
{
int t;
ll n;
scanf("%d",&t);
while(t--)
{
scanf("%lld",&n);
ll ans=n+f1(n)*f1(n)%mod*inv6%mod+f2(n)+11*n%mod*(n-1)%mod*inv12%mod;
printf("%lld
",(ans%mod+mod)%mod);
}
return 0;
}
发现网上还有更加简单的公式。
同样基于上述的表。(4) 次作差后差值恒定为 (1),说明递推式为:(f(n)=a*n^4+b*n^3+c*n^2+d*n+e),已知前 (5) 项,即可求出。
下面基于差分来解决此题:


首先,前 (7) 项为:1 5 15 35 70 126 210
在前面加上 (f(0)=0),
可以得到差分表:

所以,根据图中的 ‘利用差分表求高级等差数列的前n项和’。
可以推出:(全0行的前面行的第一个数为组合数前面的系数)
(S(n)=0*C(n+1,1)+1*C(n+1,2)+3*C(n+1,3)+3*C(n+1,4)+1*C(n+1,5))
(=frac{n*(n+1)*(n+2)*(n+3)*(n+4)}{120})
作差可以求出 (f(n)=S(n)-S(n-1)=frac{n*(n+1)*(n+2)*(n+3)}{24})。
Problem J. Prime Game
考虑每个质因子对于整体答案的贡献。
第 (p) 个位置上的数,其包含的任意一个素因子,它原本应当产生的贡献有 ((n−p+1)⋅p)。但考虑到重复,记该素因子上一次出现的位置为 (q),则此时的贡献为:((p-q)*(n-p+1))。其他的就是质因子分解,筛出 (1e3) 以内的素数,共 (168) 个,用于素因子分解。
代码:
#include <bits/stdc++.h>
#define pb push_back
using namespace std;
typedef long long ll;
const int N=1e6+6;
const int maxn=1e3+5;
int prime[200],a[N],last[N];
int cnt;
bool vis[maxn];
vector<int>fac[N];
void euler()
{
cnt=0;
for(int i=2;i<=1e3;i++)
{
if(!vis[i]) prime[++cnt]=i;
for(int j=1;j<=cnt&&prime[j]*i<=1e3;j++)
{
vis[i*prime[j]]=1;
if(i%prime[j]==0) break;
}
}
}
void divide(int num,int k)
{
for(int i=1;i<=cnt&&prime[i]*prime[i]<=num;i++)
{
if(num%prime[i]==0)
{
fac[k].pb(prime[i]);
while(num%prime[i]==0) num/=prime[i];
}
}
if(num>1) fac[k].pb(num);
}
int main()
{
euler();
int n,a;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a);
divide(a,i);
}
ll ans=0;
for(int i=1;i<=n;i++)
{
ll res=0;
for(int j=0;j<fac[i].size();j++)
{
int t=fac[i][j];
if(last[t]==0) res=1LL*i*(n-i+1);
else res=1LL*(i-last[t])*(n-i+1);
last[t]=i;
ans+=res;
}
}
printf("%lld
",ans);
return 0;
}
Problem D. Country Meow
最大值最小化问题,可以用三分枚举球心求解。
最小球覆盖:
模拟退火算法:
#include <bits/stdc++.h>
using namespace std;
const double eps = 1e-8;
const int inf = 0x3f3f3f3f;
const double start_T = 1000;
struct point3d
{
double x,y,z;
}dat[150];
int n;
double dis(point3d a, point3d b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y)+(a.z-b.z)*(a.z-b.z));
}
double solve()
{
double step=start_T,ans=inf,mt;
point3d z;
z.x=z.y=z.z=0;
int s=0;
while(step>eps)
{
for (int i = 0; i < n; ++i)
{
if (dis(z,dat[s])<dis(z,dat[i])) s=i;
}
mt=dis(z,dat[s]);
ans=min(ans,mt);
z.x+=(dat[s].x-z.x)/start_T*step;
z.y+=(dat[s].y-z.y)/start_T*step;
z.z+=(dat[s].z-z.z)/start_T*step;
step*=0.97;
}
return ans;
}
int main()
{
double ans;
cin>>n;
for (int i = 0; i < n; ++i)
scanf("%lf%lf%lf",&dat[i].x,&dat[i].y,&dat[i].z);
ans=solve();
printf("%.8f
",ans);额
return 0;
}
Problem K. Kangaroo Puzzle
因为矩阵比较小,而可以进行的操作次数远远大于矩阵大小。所以,每次选定两个1进行合并,因为一个点走,其他的点也走。每次都让选定的第一个点走到第二个点的位置,进行若干次后,一定会成功追及。
还可以采用随机化算法,生成随机数,进行 (50000) 次移动。
代码:
#include <bits/stdc++.h>
using namespace std;
char ss[30];
char c[4]={'U','D','L','R'};
int main()
{
int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%s",ss+1);
for(int i=1;i<=50000;i++)
printf("%c",c[rand()%4]);
printf("
");
return 0;
}
Problem M. Mediocre String Problem
拓展 KMP+Manacher+差分
对于从 (s) 中选出的字符串,可以分成两部分一部分与从 (t) 中选出的字符串恰好相反,一部分为回文串。
对于回文串部分,可以用 (Manacher) 在 (O(n)) 时间内求出每个位置的回文串长度。
对于另一部分,先把 (s) 串反向,然后利用拓展KMP,求出反向后的串 (s^{'}) 的每个后缀与串 (t) 的最长公共前缀,就相当找到了原串 (s) 中与 (t) 部分相反的串。
然后,就是把这两部分进行组合。
对于回文串,需要求出每个位置可以是几个回文串的起始位置。利用差分解决,从后向前进行,在每个回文串的中心位置 (+1),在结束位置的下一个位置 (-1),每次累加。
注意下标,一开始代码中 (num) 是以 (1) 为起始下标的,导致一直 (WA),(-1) 后就可以了。
代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e6 + 5;
char ss[N], t[N], sr[N];
char sn[N << 1];
int sen[N << 1], num[N];
int extend[N], nxt[N];
int init()
{
int len = strlen(ss), cnt = 1;
sn[0] = '$';
sn[1] = '#';
for (int i = 0; i < len;i++)
{
sn[++cnt] = ss[i];
sn[++cnt] = '#';
}
sn[++cnt] = '�';
return cnt;
}
void manacher()
{
int id, mx = 0;
int len = init();//扩充到的最后一个位置坐标,而不是扩充后的长度
//cout << "len=" << len << endl;
for (int i = 1; i < len;i++)
{
sen[i] = mx > i ? min(sen[2 * id - i], mx - i) : 1;
while(sn[i-sen[i]]==sn[i+sen[i]])
sen[i]++;
if(i+sen[i]>mx)
{
id = i;
mx = i + sen[i];
}
}
//差分记录:!!!!!!
for (int i = len - 2; i >= 2;i--)
{
int t = i / 2;
num[t-1]++;
num[t - (sen[i] / 2)-1]--;
}
for (int i = len / 2 - 1; i >= 1; i--)
num[i] += num[i + 1];
}
void getNext(char s[])//模式串
{
int ls=strlen(s),i=0;
nxt[0]=ls;
while(i<ls&&s[i]==s[i+1])
i++;
nxt[1]=i;
int k=1;//已知的最大匹配的开始位置
for(int i=2;i<ls;i++)
{
int len=k+nxt[k];//已知的最大匹配的结束位置
nxt[i]=min(nxt[i-k],max(0,len-i));
while(i+nxt[i]<ls&&s[nxt[i]]==s[i+nxt[i]])//如果已知的最大匹配不能满足要求,继续判断
nxt[i]++;
if(i+nxt[i]>k+nxt[k])//更新已知的最大匹配
k=i;
}
}
void getExtend(char sa[],char sb[])//主串,模式串
{//与求next数组的步骤一样,不够是两个不同的字符串之间
getNext(sb);
int i=0,la=strlen(sa),lb=strlen(sb);
while(sa[i]==sb[i]&&i<la&&i<lb)
i++;
extend[0]=i;
int k=0;
for(int i=1;i<la;i++)
{
int len=k+extend[k];
extend[i]=min(nxt[i-k],max(0,len-i));
while(i+extend[i]<la&&extend[i]<lb&&sb[extend[i]]==sa[i+extend[i]])//多了一个条件
extend[i]++;
if(i+extend[i]>k+extend[k])
k=i;
}
}
ll solve(int len)
{//注意extend从0开始存
ll ans = 0;
for (int i = 0; i <len-1;i++)
ans += 1LL*extend[len - i-1] * num[i+1];
return ans;
}
int main()
{
scanf("%s", ss);
scanf("%s", t);
manacher();
int len = strlen(ss);
for (int i = 0; i < len;i++)//先翻转ss串
sr[len - i - 1] = ss[i];
getExtend(sr, t);
printf("%lld
", solve(len));
return 0;
}
Problem E. Eva and Euro coins
归约。
以下处理基于一个结论:一个位置的 (1) 可以在不跨越 (1) 的情况下,向左移动 (k) 个位置。
对于连续的 (k) 个 (1) 可以变换成 (0)。
那么就可以把连续的 (k) 个 (0) 或者 (1) 消除。
代码:
#include <bits/stdc++.h>
using namespace std;
const int N=1e6+6;
char s[N],t[N];
int num[N][2];
int n,k;
void solve(char ss[])
{
int cnt=0;
for(int i=1;i<=n;i++)
{
num[++cnt][0]=ss[i]-'0';
num[cnt][1]=num[cnt-1][0]==ss[i]-'0'?num[cnt-1][1]+1:1;
if(num[cnt][1]==k)
cnt-=k;
}
for(int i=1;i<=n;i++)
{
if(i<=cnt) ss[i]=num[i][0]+'0';
else ss[i]='0';
}
//cout<<ss+1<<endl;
}
int main()
{
scanf("%d%d",&n,&k);
scanf("%s",s+1);
scanf("%s",t+1);
if(k==1)
{
printf("Yes
");
return 0;
}
solve(s);
solve(t);
if(strcmp(s+1,t+1)==0)
printf("Yes
");
else
printf("No
");
return 0;
}