Modular Stability

题意：

求出满足要求的数组个数：

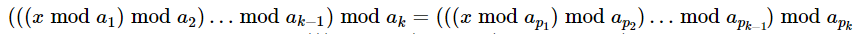
(1leq a[i] leq n，1leq a[1]<a[2]<...<a[k]leq n)，元素个数为：(k)

分析：

问题取决于最小的元素 (a[1]) 。
设 (x=n*a[1]+m)，则(x%a[1]=m)，即 (x%a[1]%a[2]%...%a[n]=m)。
要使的 (x%a[i]=m)，即 (x=a[i]*n'+m)，所以 (a[i]) 是 (a[1]) 的倍数。
所以，可以枚举 (a[1]) 的取值，剩下的 (k-1) 个数在其倍数中选择，最终的结果为：(sum_{i=1}^{n}{C(frac{n}{i}-1,k-1)})。
需要预处理出阶乘逆元：(inv[i]=inv[i+1]*(i+1))

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=998244353;
const int N=5e5+5;
ll inv[N],fac[N];
ll power(ll a,ll b)
{
    ll res=1;
    while(b)
    {
        if(b&1) res=res*a%mod;
        b>>=1;
        a=a*a%mod;
    }
    return res%mod;
}
void init()
{
    fac[0]=1;
    for(int i=1;i<=5e5;i++)
        fac[i]=(fac[i-1]*i)%mod;
    int t=5e5;
    inv[t]=power(fac[t],1LL*(mod-2));
    for(int i=t-1;i>=0;i--)//注意要到0,会用到inv[0]
        inv[i]=inv[i+1]*(i+1)%mod;
}
ll C(int x,int y)
{
    if(x<y) return 0;
    ll res=1;
    y=min(x-y,y);
    for(int i=x;i>=x-y+1;i--)
        res=res*i%mod;
    res=res*inv[y]%mod;
    return res;
}
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    ll ans=0;
    init();
    for(int i=1;i<=n;i++)
        ans=(ans+C(n/i-1,k-1))%mod;
    printf("%lld
",ans);
    return 0;
}