FFT

( ext{Fast Fourier Transformation})（快速傅里叶变换），用来加速多项式乘法。朴素算法的时间复杂度：(O(n^2))，而 ( ext{FFT}) 则为 (nlog n)。

多项式的系数表示法和点值表示法

( ext{FFT}) 其实是一个用 (O(nlog_2n)) 的时间将一个用系数表示的多项式转换成它的点值表示的算法。

系数表示法

一个 (n) 次的多项式 (f(x)) 可以表示为:

[f(x)=sum_{i=0}^{n}{a_ix^i} ]

即可以用每一项的系数来表示 (f(x))：

[f(x)={a_0,a_1,dots,a_{n-1},a_{n} } ]

点值表示法

点值表示法是把这个多项式看成一个函数，放在平面直角坐标系中，从上面选取 (n+1) 个点，那么这 (n+1) 个点就可以唯一确定该多项式，也就是有且仅有一个多项式满足：(forall k,f(x_k)=y_k)，从而利用这 (n+1) 个点来唯一地表示这个函数。因为，将这 (n+1) 个点的坐标代入，可以得到一个(n+1) 条 (n+1) 元的线性方程组，有唯一解。

即：

[f(x)={(x_0,f(x_0)),(x_1,f(x_1)),dots,(x_n,f(x_n)) } ]

通俗地说，多项式由系数表示法转为点值表示法的过程，就是 ( ext{DFT}) 的过程。相对地，把一个多项式的点值表示法转化为系数表示法的过程，就是 ( ext{IDFT})。而 ( ext{FFT}) 就是通过取某些特殊的 (x) 的点值来加速 ( ext{DFT}) 和 ( ext{IDFT}) 的过程。

对于用系数表示的两个多项式，相乘的复杂度为：(O(n^2))，而用点值表示的多项式相乘则需要 (O(n))。

假设两个多项式的点值表示如下：

[f(x)={(x_0,f(x_0)),(x_1,f(x_1)),dots,(x_n,f(x_n)) }\ g(x)={(x_0,g(x_0)),(x_1,g(x_1)),dots,(x_n,g(x_n)) }\ ]

若它们的乘积为 (h(x))，则：

[h(x)={(x_0,f(x_0) imes g(x_0)),(x_1,f(x_1) imes g(x_1)),dots,(x_n,f(x_n) imes g(x_n)) } ]

目测复杂度为 (O(n))。

但是朴素的系数表示法转点值表示法的算法还是 (O(n^2)) 的，逆过程也是如此，即 ( ext{DFT}) 和 ( ext{IDFT})。

复数

对于任意系数多项式转点值，当然可以取任意 (n) 个 (x) 值代入计算，但是暴力计算 (x_k^0,x_k^1,cdots,x_k^{n-1}) 的复杂度还是 (O(n^2)) 的。可以代入一组特殊的 (x) ，用来简化计算。因此，我们不要去算 (x^i)，可以发现 (-1) 和 (1) 的幂很好算，但是只有两个完全不够，至少需要 (n) 个，使得 (x) 的若干次方等于 (pm1)。联系到虚数，长度为 (1) 的虚数，不管怎么乘，长度都是 (1)，即下图圆（以原点为圆心，(1) 为半径的单位圆）上的点均满足要求。

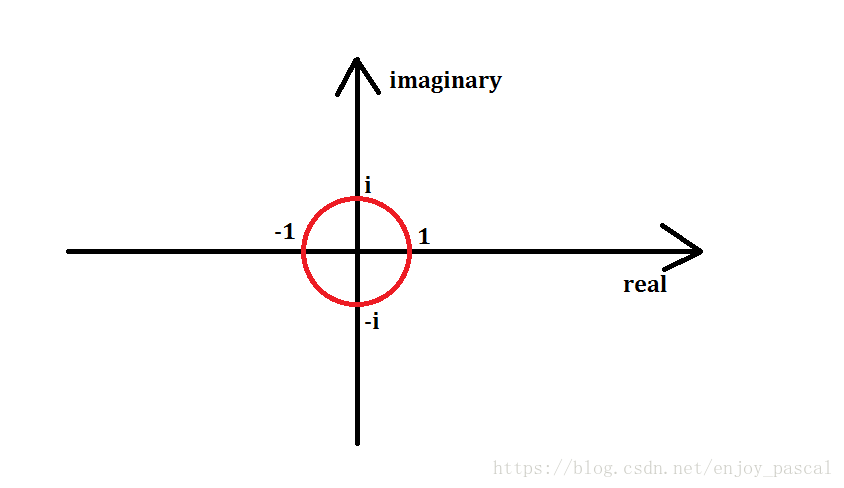
同时，在此处要求 (n) 为 (2) 的次幂，且要把圆进行 (n) 等分。

复数的运算

设两个复数：(z_1=a+bi,z_2=c+di)，

则：

[z_1+z_2=(a+c)+(b+d)i\ z_1-z_2=(a-c)+(b-d)i\ z_1 imes z_2=(ac-bd)+(ad+bc)i ]

复数相加满足平行四边形法则。

复数相乘的小性质：

[(alpha_1, heta_1)*(alpha_2, heta_2)=(alpha_1alpha_2, heta_1+ heta_2) ]

即模长相乘，极角相加。

复根

我们称 (x^n=1) 在复数意义下的解是 (n) 次单位复根，显然这样的解有 (n) 个。设 (omega_n^k=e^{frac{2pi ki}{n}})，则 (x^n=1) 的解集为 ({omega_n^k|k=0,1,cdots,n-1 })。根据复平面的知识，(n) 次单位复根是复平面把单位圆 (n) 等分的第一个角所对应的向量。其他复根均可以用单位复根的幂表示。

同时，根据欧拉公式，有：

[omega_n=e^{frac{2pi i}{n}}=cosleft(frac{2pi}{n} ight)+i·sinleft(frac{2pi}{n} ight) ]

如下图中，(n=4) 时，(omega_n=i) 就是 (4) 次单位复根。

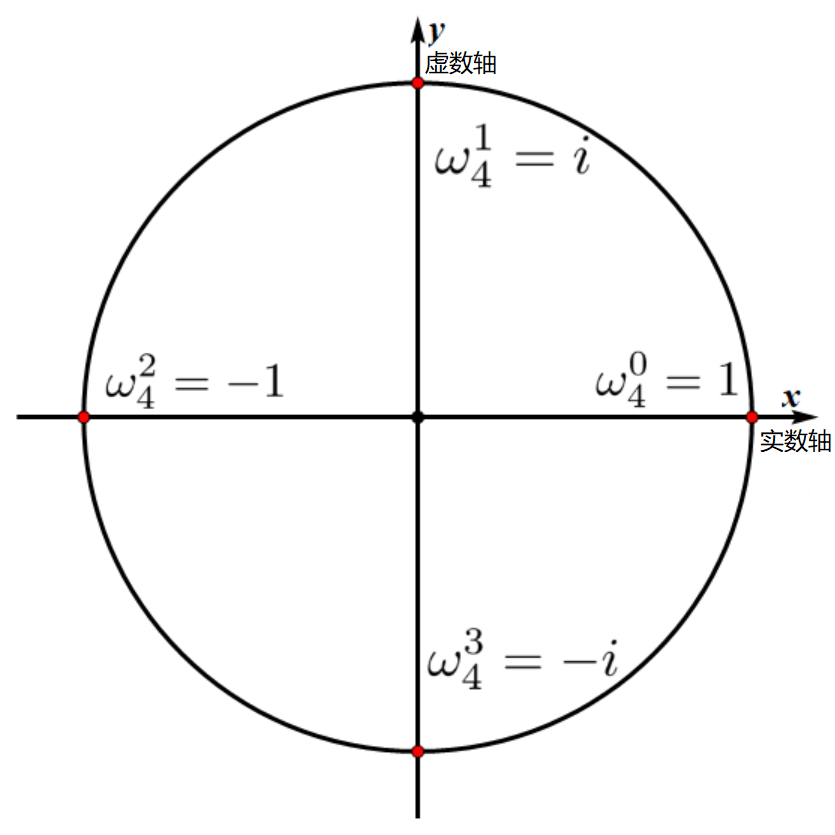
将圆上的点从 ((1,0)) 开始逆时针进行编号（从 (0) 开始），记编号为 (k) 的点代表的复数值为 (omega_n^k)，根据复数相乘的性质，有：

[(omega^1_n)^k=omega^k_n ]

其中，(omega^1_n) 称为 (n) 次单位复根，而且每一个 (omega) 都可以求出（欧拉公式）。

[omega^k_n=cosleft(frac{k}{n}2pi ight)+i· sinleft(frac{k}{n}2pi ight) ]

那么，(omega_n^0,omega_n^1,omega_n^2,dots,omega_n^{n-1}) 就是要代入 (x_0,x_1,x_2,dots ,x_{n-1}) 的值。

单位复根的性质

• (omega_n^k=omega_{2n}^{2k})

• (omega_n^{k+frac{n}{2}}=-omega_n^k)

• (omega_n^0=omega_n^n=1)

上述性质结合图理解应该很好理解，证明的话要利用上面的 (omega_n^k) 的公式。

以上，我们只是对 (x_i) 取了一些特殊的值，但最后由 (h(x)) 的点表示法求系数表示法时，还是要将值代入 (O(n^2)) 去算。

分治

利用分治来进行 ( ext{DFT}) ，就得到了 ( ext{FFT})。

设多项式 (A(x)) （(n) 为偶数）:

[A(x)=sum_{i=0}^{n-1}{a_ix^i}=a_0+a_1x+a_2x^2+dots+a_{n-1}x^{n-1} ]

按幂的奇偶来将多项式划分为两部分，然后右边提出一个 (x)：

[f(x)=(a_0+a_2x^2+a_4x^4+dots+a_{n-2}x^{n-2})+x(a_1+a_3x^2+a_5x^4+dots+a_{n-1}x^{n-2}) ]

可以发现，两边很相似，可以再设两个多项式：(A_1(x),A_2(x))，有：

[A_1(x)=a_0+a_2x+a_4x^2+dots+a_{n-2}x^{frac{n-2}{2}}\ A_2(x)=a_1+a_3x+a_5x^2+dots+a_{n-1}x^{frac{n-2}{2}} ]

可以得出：

[A(x)=A_1(x^2)+xA_2(x^2) ]

假设 (k<frac{n}{2})，将 (omega_n^k) 作为 (x) 代入到 (A(x)) 中，有：

[egin{align} A(omega_n^k) &= A_1(omega_n^{2k})+omega_n^kA_2(omega_n^{2k})\ &=A_1(omega_{frac{n}{2}}^k)+omega_{n}^kA_2(omega_{frac{n}{2}}^k) end{align} ]

再将 (omega_{n}^{k+frac{n}{2}}) 作为 (x) 代入到 (A(x)) 中，有：

[egin{align} A(omega_{n}^{k+frac{n}{2}}) &=A_1(omega_{n}^{2k+n})+omega_{n}^{k+frac{n}{2}}A_2(omega_{n}^{2k+n})\ &=A_1(omega_{n}^{2k}omega_{n}^{n})-omega_{n}^{k}A_2(omega_{n}^{2k}omega_n^n)\ &=A_1(omega_frac{n}{2}^k)-omega_n^kA_2(omega_{frac{n}{2}}^k) end{align} ]

对比上述的两个式子可以发现，只是加减的不同，只要求出了 (A_1(omega_frac{n}{2}^k)) 和 (omega_n^kA_2(omega_{frac{n}{2}}^k)) 的值，就可以同时获得 (A(omega_n^k)) 和 (A(omega_{n}^{k+frac{n}{2}})) 的值。如果采用递归分治的方式来实现，每次回溯的时候只扫前面一半的序列，即可得出后面一半序列的答案。(n=1) 时，只有一个常数，直接( ext{return}) 即可，复杂度：(O(nlog_2n))。

IFFT（快速傅里叶逆变换）

通过 ( ext{FFT}) ，我们可以得出两个多项式相乘的积的点值表示法，接下来考虑如何将点值表示法转化为系数表示法。

IDFT

将单位复根代入多项式后，可得：

[left[ egin{matrix} y_0\ y_1\ y_2\ y_3\ vdots \ y_{n-1} end{matrix} ight]= left[ egin{matrix} 1 &1 &1 &1 &cdots &1\ 1 &omega_n^1 &omega_n^2 &omega_n^3 &cdots &omega_n^{n-1}\ 1 &omega_n^2 &omega_n^{4} &omega_n^6 &cdots &omega_n^{2(n-1)}\ 1 &omega_n^3 &omega_n^{6} &omega_n^9 &cdots &omega_n^{3(n-1)}\ vdots &vdots &vdots &vdots &ddots &vdots\ 1 &omega_n^{n-1} &omega_n^{2(n-1)} &omega_n^{3(n-1)} &cdots &omega_n^{(n-1)^2}\ end{matrix} ight] left[ egin{matrix} a_0\ a_1\ a_2\ a_3\ vdots\ a_{n-1} end{matrix} ight] ]

其中，代入的 (x_i=omega_n^i)。

现在，我们已知最左边的值和中间的大矩阵中 (x) 对应的各个值。根据矩阵的知识可以知道，只要在左右两边同时左乘上中间大矩阵的逆矩阵，即可求出系数矩阵。而中间的矩阵的元素十分的特殊，因此其逆矩阵也具有特殊的性质：即每一项取倒数，再乘上 (n) ，就可以得到其逆矩阵（这就是为什么要代入 (omega_n^i) 的原因）。

为了取倒数，根据单位复根的性质和欧拉公式，有：

[frac{1}{omega_n}=omega_n^{-1}=e^{-frac{2pi i}{n}}=cosleft(frac{2pi}{n} ight)-i·sinleft(frac{2pi}{n} ight) ]

其中，(i) 是虚数单位，欧拉公式：(e^{ix}=cos(x)+isin(x))。

取倒数时，每一项乘上单位根的共轭复数即可。然后再分别乘上 (n) 就可以得到逆矩阵。

结论：一个多项式在分治过程中乘上单位复根的共轭复数，分治完的每一项除以 (n) 即为原多项式的每一项系数。也就说 ( ext{FFT}) 和 ( ext{IFFT}) 可以同时进行。

( ext{C++}) 有自带的复数模板：( ext{complex库})。( ext{a.real()}) 即表示复数 (a) 的实部，( ext{a.imag()}) 表示虚部。

由于递归的写法常数比较大，因此此处只给出非递归的形式。

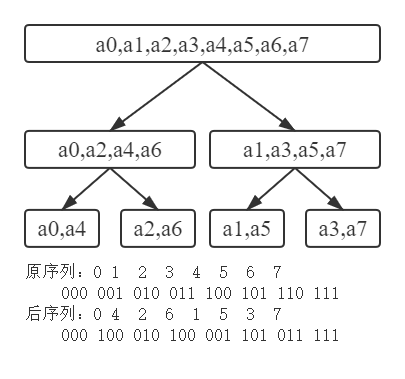
观察上图可以发现规律：原来的那个序列，每个数用二进制表示，然后把二进制翻转对称一下，就是最终那个位置的下标。该变换称为 蝴蝶变换。实际上，蝴蝶变换可以 (O(n)) 从小到大递推实现，设 (len=2^k)，其中 (k) 表示二进制数的长度，设 (R(x)) 表示长度为 (k) 的二进制数 (x) 翻转后的数（高位补 (0)）。那么，我们要求的是：(R(0),R(1),cdots,R(n-1))。

蝴蝶变换

首先，有 (R(0)=0)。

从小到大求 (R(x))，那么当求 (R(x)) 时，(R(lfloorfrac{x}{2} floor)) 是已知的。因此，我们把 (x) 右移一位（除以 (2)），然后取反，再右移一位，就可以得到 (x) 除了二进制最低位外其它位的翻转结果。考虑最低位翻转的结果，若为 (0) 则，则翻转后最高位是 (0) ；否则为 (1)，那么还要加上 (frac{len}{2}=2^{k-1})。

综上所述：

[R(x)=left lfloor frac{R(lfloor frac{x}{2} floor)}{2} ight floor+(x mod 2) imesfrac{len}{2} ]

蝴蝶变换模板

// 需要保证 len 是 2 的幂
// 记 rev[i] 为 i 翻转后的值
void change(cp *pn, int len) 
{
	for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
    for(int i=0;i<len;i++)
    {
        if(i<rev[i]) swap(pn[i],pn[rev[i]]);
    }
}

这样的话，就可以预先处理好每个位置的最终位置，再一步步的向上合并，复杂度：(O(n))。

模板

loj108多项式乘法

输入 (n) 和 (m)，分别表示两个多项式的最高项次数。

(0leq n,m leq 10^5)

采用 ( ext{C++}) 自带的 ( ext{complex}) 复数类，但运行没有自己写快。

#include<bits/stdc++.h>
#define N 2621450
#define pi acos(-1) 
using namespace std;
typedef complex<double> E;
int n,m,l,r[N];
E a[N],b[N];
void fft(E *a,int f){
    for(int i=0;i<n;i++)if(i<r[i])swap(a[i],a[r[i]]);
    for(int i=1;i<n;i<<=1){
        E wn(cos(pi/i),f*sin(pi/i)); 
        for(int p=i<<1,j=0;j<n;j+=p){
            E w(1,0);
            for(int k=0;k<i;k++,w*=wn){
                E x=a[j+k],y=w*a[j+k+i];
                a[j+k]=x+y;a[j+k+i]=x-y;  
            }
        }
    }
}
inline int read(){
    int f=1,x=0;char ch;
    do{ch=getchar();if(ch=='-')f=-1;}while(ch<'0'||ch>'9');
    do{x=x*10+ch-'0';ch=getchar();}while(ch>='0'&&ch<='9');
    return f*x;
}
int main(){
    n=read();m=read();
    for(int i=0;i<=n;i++)a[i]=read();
    for(int i=0;i<=m;i++)b[i]=read();
    m+=n;for(n=1;n<=m;n<<=1)l++;
    for(int i=0;i<n;i++)r[i]=(r[i>>1]>>1)|((i&1)<<(l-1));
    fft(a,1);fft(b,1);
    for(int i=0;i<=n;i++)a[i]=a[i]*b[i];
    fft(a,-1);
    for(int i=0;i<=m;i++)printf("%d ",(int)(a[i].real()/n+0.5));
}

自己构造结构体表示复数，比直接用库快一点。

#include <bits/stdc++.h>

using namespace std;
const int N=1e5+5;
const double pi=acos(-1);
int a[N],b[N],rev[N<<2];
struct cp
{
    double x,y;
    cp(double tx=0.0,double ty=0.0)
    {
        x=tx;
        y=ty;
    }
    cp operator +(const cp &t)const
    {
        return cp(x+t.x,y+t.y);
    }
    cp operator -(const cp &t)const
    {
        return cp(x-t.x,y-t.y);
    }
    cp operator *(const cp &t)const
    {
        return cp(x*t.x-y*t.y,x*t.y+y*t.x);
    }
}A[N<<2],B[N<<2];
void read(int &x)
{
    x=0;
    int f=1;
    char ch;
    ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') f=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        x=(x<<3)+(x<<1)+ch-'0';
        ch=getchar();
    }
    x*=f;
}
void swp(cp &u,cp &v)
{//交换记得要用引用
    cp t=u;
    u=v;
    v=t;
}
//f=1:FFT,f=-1:IFFT
void FFT(cp *pn,int len,int f)
{
    for(int i=0;i<len;i++)
        if(i<rev[i]) swp(pn[i],pn[rev[i]]);
    for(int i=1;i<len;i<<=1)//模拟合并过程，根据分治的公式理解
    {
        cp wn(cos(pi/i),f*sin(pi/i));//求单位复根，此时n=2*i
        for(int j=0,d=(i<<1);j<len;j+=d)
        {
            cp w(1,0);
            for(int k=0;k<i;k++)
            {
                cp u=pn[j+k],v=w*pn[j+k+i];
                pn[j+k]=u+v,pn[j+k+i]=u-v;
                w=w*wn;
            }
        }
    }
    if(f==-1)//IFFT
    {
        for(int i=0;i<len;i++)
            pn[i].x/=len;
    }
}
int main()
{
    int n,m;
    read(n),read(m);
    for(int i=0;i<=n;i++) read(a[i]);
    for(int i=0;i<=m;i++) read(b[i]);
    int len=1,cnt=0;
    while(len<n+m+1)//保证len是2的整数次幂
    {
        len<<=1;
        cnt++;
    }
    //先求出变换后位置:
    for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
    for(int i=0;i<len;i++)
    {
        if(i<=n) A[i]=cp(a[i],0);
        else A[i]=cp(0,0);
        if(i<=m) B[i]=cp(b[i],0);
        else B[i]=cp(0,0);
    }
    //系数表示转点值表示：
    FFT(A,len,1);
    FFT(B,len,1);
    //求出最终结果的点值表示：
    for(int i=0;i<len;i++)
        A[i]=A[i]*B[i];
    //点值表示转系数表示：
    FFT(A,len,-1);
    for(int i=0;i<=n+m;i++)
        printf("%d%c",(int)(A[i].x+0.5),i==n+m?'
':' ');
    return 0;
}

参考博客：

https://blog.csdn.net/enjoy_pascal/article/details/81478582?depth_1-

https://oi-wiki.org/math/poly/fft/

FFT 字符串匹配

FFT还能字符串匹配？

假设现在又两个字符串：(S,T),令 (n=|S|,m=|T|)，且有 (ngeq m)，串都从 (0) 开始存。

若 (S) 串的从第 (i) 个字符开始和 (T) 串匹配，即：

[sum_{j=0}^{m-1}{(S[i+j]-T[j])=0} ]

但是，上式还存在问题。因为受到正负的影响，可能导致 'ab'='ba' 的情况出现。

因此，对上式进行改变，有：

[sum_{j=0}^{m-1}{(S[i+j]-T[j])^2} (0leq j<m) ]

当其为 (0) 时，就可以表示 (S) 的一个子串和 (T) 匹配。

但是上式仍然没有什么特殊之处，继续变换。将 (T) 串进行前后翻转，那么当 (S) 从位置 (i) 开始和 (T) 串匹配时，就有：(S[i]=T[m-1],S[i+j]=T[m-1-j],cdots) ，因此当满足下列公式：

[sum_{j=0}^{m-1}{(S[i+j]-T[m-1-j])^2}=0 ]

可以说明达到匹配。

可以发现：(i+j+m-1-j=m-i-1) 是一个定值，即多项式乘法 (F=S*T) 的 (F(m-i-1)) 就可以表示 (S[i,i+1,cdots]) 和串 (T[0,1,2,cdots,m-1]) 的匹配情况。将平方拆开，得到 (3) 个多项式的和的形式：

[sum_{j=0}^{m-1}{(S[i+j]-T[m-1-j])^2}=sum_{j=0}^{m-1}{S[i+j]^2}+sum_{j=0}^{m-1}{T[m-1-j]^2}-2·sum_{j=0}^{m-1}{(S[i+j]*T[m-1-j])} ]

前两项，可以直接预处理前缀和。对于后面的一项，可以令：

[g(i)=2*sum_{j=0}^{m-1}{(S[i+j]*T[m-1-j])} ]

枚举 (i) ，求出每个 (g(i))，这个就可以用 ( ext{FFT}) 来优化了，复杂度：(O(nlog_2n))。

复杂度还没有KMP优秀

Rock Paper Scissors Lizard Spock.

https://nanti.jisuanke.com/t/A1676

枚举胜利的情况，把答案累加起来。此时，只需要计算 (g(i)) 即可（我把整个式子都算出来，死活调不对）。

代码

#include <bits/stdc++.h>

using namespace std;
typedef pair<char,char>pcc;
const double pi=acos(-1);
const int N=1e6+5;
typedef long long ll;
char s[N],t[N];
pcc f[13];
int rev[N<<2],res[N<<2];
struct cp
{
    double x,y;
    cp (double tx=0.0,double ty=0.0)
    {
        x=tx;
        y=ty;
    }
    cp operator +(const cp &t)const
    {
        return cp(x+t.x,y+t.y);
    }
    cp operator -(const cp &t)const
    {
        return cp(x-t.x,y-t.y);
    }
    cp operator *(const cp &t)const
    {
        return cp(x*t.x-y*t.y,x*t.y+y*t.x);
    }
}A[N<<2],B[N<<2];
void init()
{//胜利的情况
    f[1]=make_pair('S','P');
    f[2]=make_pair('S','L');
    f[3]=make_pair('P','R');
    f[4]=make_pair('P','K');
    f[5]=make_pair('R','L');
    f[6]=make_pair('R','S');
    f[7]=make_pair('L','P');
    f[8]=make_pair('L','K');
    f[9]=make_pair('K','R');
    f[10]=make_pair('K','S');
}
void swp(cp &u,cp &v)
{
    cp t=u;
    u=v;
    v=t;
}
void FFT(cp *pn,int len,int f)
{
    for(int i=0;i<len;i++)
        if(i<rev[i]) swp(pn[i],pn[rev[i]]);
    for(int i=1;i<len;i<<=1)
    {
        cp wn(cos(pi/i),f*sin(pi/i));
        for(int j=0,d=(i<<1);j<len;j+=d)
        {
            cp w(1,0);
            for(int k=0;k<i;k++)
            {
                cp u=pn[j+k],v=w*pn[j+k+i];
                pn[j+k]=u+v,pn[j+k+i]=u-v;
                w=w*wn;
            }
        }
    }
    if(f==-1)
    {
        for(int i=0;i<len;i++)
            pn[i].x/=len;
    }
}
int main()
{
    init();
    scanf("%s",s);
    scanf("%s",t);
    int n=strlen(s),m=strlen(t);
    int ans=0,len=1,maxn=n+m+1,cnt=0;
    while(len<maxn)
    {
        len<<=1;
        cnt++;
    }
    for(int i=0;i<len;i++)
        rev[i]=(rev[i>>1]>>1)|((i&1)<<(cnt-1));
    reverse(t,t+m);
    for(int i=1;i<=10;i++)
    {
        for(int j=0;j<len;j++)
            A[j]=cp(0,0),B[j]=cp(0,0);
        for(int j=0;j<m;j++)
        {
            if(t[j]==f[i].first)
                A[j]=cp(1,0);
        }
        for(int j=0;j<n;j++)
        {
            if(s[j]==f[i].second)
                B[j]=cp(1,0);
        }
        FFT(A,len,1);
        FFT(B,len,1);
        for(int j=0;j<len;j++) A[j]=A[j]*B[j];
        FFT(A,len,-1);
        for(int j=0;j<=len;j++)
            res[j]+=(int)(A[j].x+0.5);
    }
    for(int i=m-1;i<n;i++)//根据公式，i从m-1开始
        ans=max(ans,res[i]);
    printf("%d
",ans);
    return 0;
}