Kruskal算法: 相对于prim算法,适合于求边稀疏的网的最小生成树
Prim算法: 适合于求边稠密的网的最小生成树
Prim算法:
时间复杂度O(n2) ,与网中的边数无关
假设N=(V,{E})是连通图,TE是N上最小生成树中边的集合。算法从U={u0} (u0属于V),TE={} 开始,重复执行下述操作:
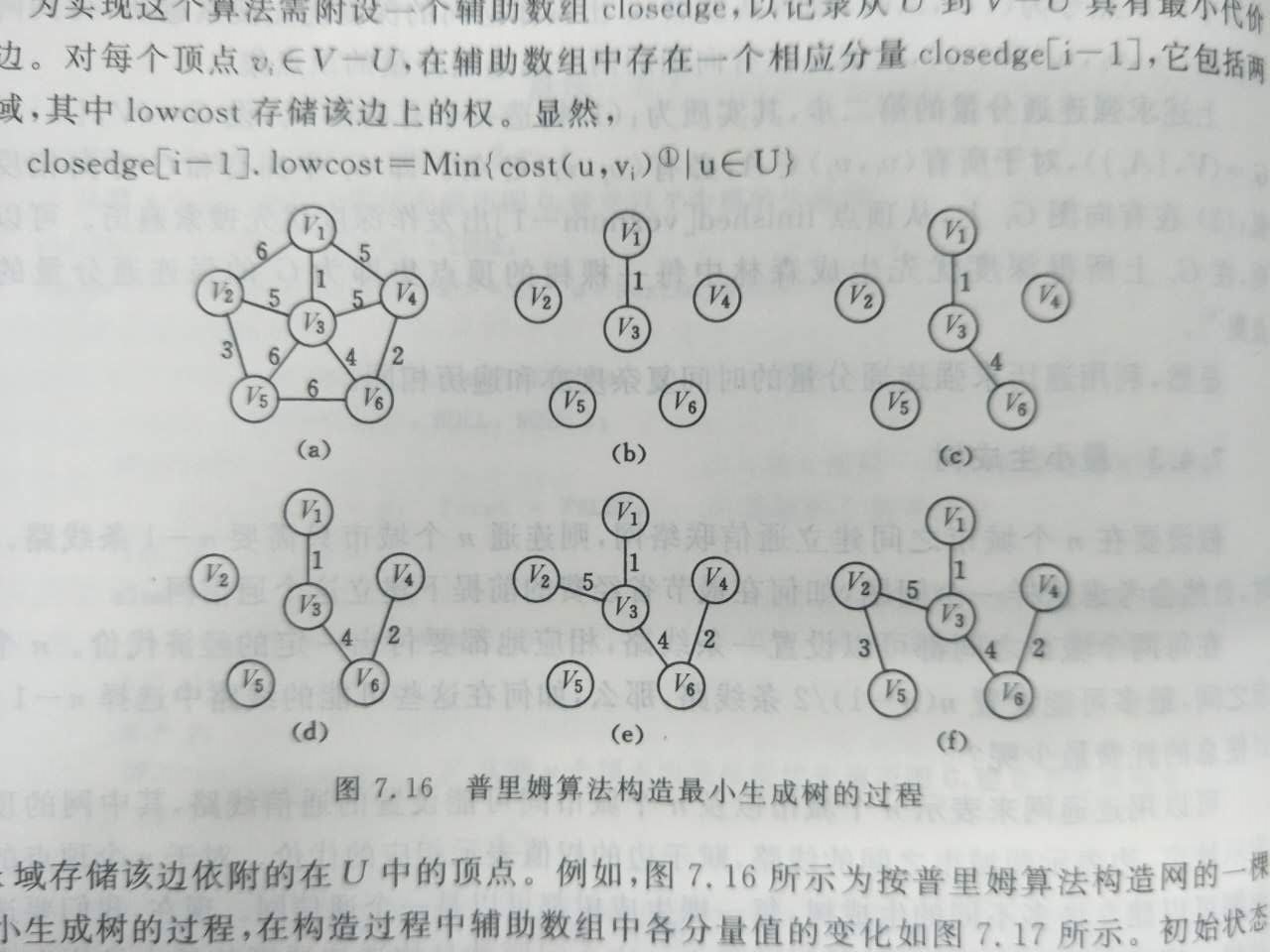
在所有u属于U,v属于V-U的边(u,v)属于E中找一条代价最小的边(u0,v0)并入集合TE,同时v0并入U,直至U=V为止。此时TE中必有n-1条边,则T=(V,{TE})为N的最小生成树。
Kruskal算法:
时间复杂度O(eloge)
假设连通图N=(V,{E}),则令最小生成树的初始状态为只有n个顶点而无边的非连通图T=(V,{}),图中每个顶点自成一个连通分量。
在E中选择代价最小的边,若该边依附的顶点落在T中不同的连通分量上,则将此边加入到T中,否则舍去此边而选择下一条代价最小的边。以此类推,直至T中所有顶点都在同一连通分量上为止。
