递推与记忆化搜索

　内容参考书籍《算法竞赛入门到进阶》

先看一道经典题：poj1163 http://poj.org/problem?id=1163

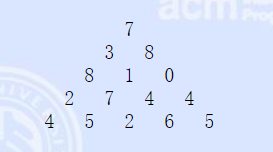
 如果此题按照从上往下的方法计算，每走一步下一步就有2种选择，其复杂度为2ⁿ

那么我们从下往上算，下面给出dfs代码：

int dfs(int i,int j)
{
	if (i == n) return a[i][j];//递归到最后一行返回
	return dp[i][j] = max(dfs(i+1,j),dfs(i+1,j+1))+ a[i][j];
}

从1,1开始往下走，一直到最后一行，返回，每一次取能走到该点的最大值加上该点，继续返回，代码很好理解，只是复杂度为2ⁿ

下面我们再来讲一下递推，代码如下：

　　for (int j = 1; j <= n; ++j) dp[n][j] = a[n][j];
　　for (int i = n-1; i >= 1; --i)
　　{
　　　　for (int j = 1; j <= i; ++j)
　　　　{
	　　dp[i][j] = max(dp[i+1][j],dp[i+1][j+1]) + a[i][j];
　　　　}
　　}
　　cout<<dp[1][1]<<endl;

首先是第一层循环，将三角形最下面一层全部赋值给dp，然后从下往上求解，输出dp[1][1]即是最大值。这样复杂度便只有n²

那么搜索可以做到吗？当然可以，这就是我们说的记忆化，只需要在搜索算法中加入if即可，代码如下：

int dfs(int i,int j)
{
	if (i == n) return a[i][j];//递归到最后一行返回
	if (dp[i][j] >= 0) return dp[i][j];//记忆
	return dp[i][j] = max(dfs(i+1,j),dfs(i+1,j+1))+ a[i][j];
}

　这样搜索算法的复杂度也降到了n²，为什么要加这样一句话呢?我们可以发现，当我们从第2层的“3”往下走会经过“1”,计算一次从1出发的递归；从第2层的“8”往下走也会经过“1”，又重新计算了“1”出发的递归，为了避免这样的重复，使用记忆化便能避免，从而降低复杂度。