链表有环问题,可以采用两个指针,分别以不同的速度遍历链表,如果存在环,那么快指针和慢指针一定会有相遇的时候,这与以前的数学上得追及问题很类似。
若一个带环链表如下:
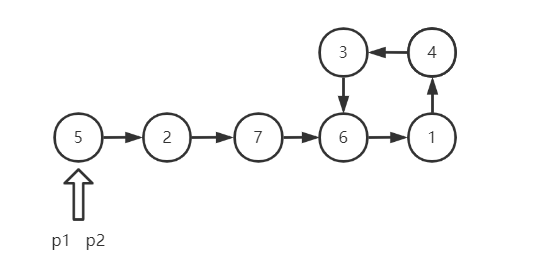
分别定义两个指针p1和p2,p1以每次向后移动一个节点,而p2每次向后移动两个结点,在第一次移动中p1指向结点2,p2指向结点7,第二次p1指向结点7,p2指向结点1,第三次p1指向结点6,p2指向结点3,第四次p1指向结点1,p2指向结点1。他们指向了同一个结点,说明该链表一定存在环。
对于上面分析对是否存在环的代码实现:
public class LinkedCycle { static class Node{ int data; Node next; public Node(int data) { this.data = data; } } public static boolean isCycle(Node node){ // 两个指针 Node p1 = node; Node p2 = node; while (p1 != null && p2.next != null){ p1 = p1.next; p2 = p2.next.next; if(p1 == p2){ return true; } } return false; } public static void main(String[] args) { Node node = new Node(5); Node node1 = new Node(2); Node node2 = new Node(7); Node node3 = new Node(6); Node node4 = new Node(1); Node node5 = new Node(4); Node node6 = new Node(3); node.next = node1; node1.next = node2; node2.next = node3; node3.next = node4; node4.next = node5; node5.next = node6; node6.next = node3; System.out.println(isCycle(node)); } }
其时间复杂度是O(n),空间是O(1)。
求入环节点:
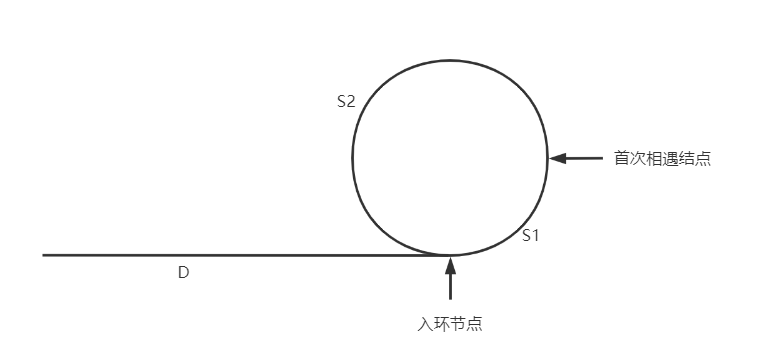
假设存在如上的关系,从链表的首节点到入环节点的距离是D,入环节点到首次相遇的节点距离是S1,首次相遇节点回到入环节点的距离是S2。那么当两个指针首次相遇,慢指针P1所走的路程是D+S1。快指针P2一定是比慢指针多走了N(n>=1)圈,所走的路程是:D+S1+(S2+S1)*N。
由于快指针P2每次比P1多走一个节点,那么他走的路程一定是p1的二倍。即 2(D+S1)= D+S1+(S1+S2)N ----------> D = (N-1)(S1+S2)+S2。 由该关系可以得出,当N等于1时,D=S2,也就是首次相遇结点再回到入环节点的距离等于链表的首节点到入环节点的距离。即只需要让其中一个指针回到链表头,另一个继续从首次相遇结点向后走,这次两个指针都是一个节点一个节点的走,再次相遇就是入环节点。
public static Node findInterNode(Node node){ // 首次相遇结点(根据是否存在环可以得到该节点) Node p1 = firstMeetingNode; // 链表头 Node p2 = node; // 入环结点 Node interNode = null; while (p1 != null&&p2 != null){ p1 = p1.next; p2 = p2.next; if(p1 == p2){ interNode = p1; break; } } return interNode; }