
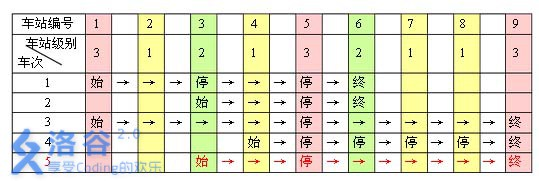
题目描述 一条单向的铁路线上,依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点) 例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。 现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。 输入输出格式 输入格式: 输入文件为 level.in。 第一行包含 2 个正整数 n, m,用一个空格隔开。 第 i + 1 行(1 ≤ i ≤ m)中,首先是一个正整数 si(2 ≤ si ≤ n),表示第 i 趟车次有 si 个停靠站;接下来有 si个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。 输出格式: 输出文件为 level.out。 输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。 输入输出样例 输入样例#1: 9 2 4 1 3 5 6 3 3 5 6 输出样例#1: 2 输入样例#2: 9 3 4 1 3 5 6 3 3 5 6 3 1 5 9 输出样例#2: 3 说明 对于 20%的数据,1 ≤ n, m ≤ 10; 对于 50%的数据,1 ≤ n, m ≤ 100; 对于 100%的数据,1 ≤ n, m ≤ 1000。
芒果君:拓扑排序还是很容易看出来的(毕竟好多奇奇怪怪的题最后都变成图论了……),关系也很好建立,被跳过的站点比没跳过的优先级低,那就暴力建边。之前求拓扑排序都是栈模拟,这次没换dfs之前T了3个点。以后就都用dfs了。
#include<cstdio> #include<cmath> #include<ctime> #include<cstring> #include<iostream> #include<algorithm> #include<queue> #include<stack> #include<vector> #define maxn 1010 #define inf 1<<29 using namespace std; typedef long long ll; vector<int>Edge[maxn]; stack<int>S; int ans,n,m,st,ed,rm,num,rec[maxn],tmp[maxn]; bool vis[maxn][maxn]; inline int read() { char ch=getchar(); int x(0); while(ch<'0'||ch>'9') ch=getchar(); while(ch>='0'&&ch<='9'){ x=x*10+ch-'0'; ch=getchar(); } return x; } void dfs(int x) { if(rec[x]) return; rec[x]=1; for(int i=0;i<Edge[x].size();++i){ dfs(Edge[x][i]); rec[x]=max(rec[x],rec[Edge[x][i]]+1); } ans=max(ans,rec[x]); } int main() { scanf("%d%d",&n,&m); rm=n; while(m--){ num=read(); for(int i=1;i<=num;++i) tmp[i]=read(); for(int i=1;i<num;++i) for(int j=tmp[i]+1;j<tmp[i+1];++j) for(int k=1;k<=num;++k) if(!vis[j][tmp[k]]) Edge[j].push_back(tmp[k]),vis[j][tmp[k]]=1; } for(int i=1;i<=n;++i) if(!rec[i]) dfs(i); printf("%d ",ans); return 0; }
