Problem Description
For a tree, which nodes and edges are all weighted, the ratio of it is calculated according to the following equation.
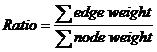
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
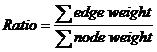
Given a complete graph of n nodes with all nodes and edges weighted, your task is to find a tree, which is a sub-graph of the original graph, with m nodes and whose ratio is the smallest among all the trees of m nodes in the graph.
Input
Input contains multiple test cases. The first line of each test case
contains two integers n (2<=n<=15) and m (2$lt;=m<=n), which
stands for the number of nodes in the graph and the number of nodes in
the minimal ratio tree. Two zeros end the input. The next line
contains n numbers which stand for the weight of each node. The
following n lines contain a diagonally symmetrical n×n connectivity
matrix with each element shows the weight of the edge connecting one
node with another. Of course, the diagonal will be all
0, since there is no edge connecting a node with itself.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
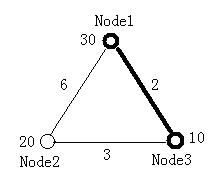
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.
All the weights of both nodes and edges (except for the ones on the diagonal of the matrix) are integers and in the range of [1, 100].
The figure below illustrates the first test case in sample input. Node 1 and Node 3 form the minimal ratio tree.

Output
For each test case output one line contains a sequence of the m nodes
which constructs the minimal ratio tree. Nodes should be arranged in
ascending order. If there are several such sequences, pick the one which
has the smallest node number; if there's a tie,
look at the second smallest node number, etc. Please note that the
nodes are numbered from 1 .
Sample Input
3 2
30 20 10
0 6 2
6 0 3
2 3 0
2 2
1 1
0 2
2 0
0 0
Sample Output
1 3
1 2
题目大意:
有一个n个点的图, 然后给出n*n的邻接矩阵图, 要求这个图的m个结点的子图,使得这个子图所有边之和与所有点之和的商值最小。
分析与总结:
直接dfs枚举出n个点所有的m个点的组合,然后对m个点求最小生成树,便可得出答案。
dfs枚举n个点的m个点组合,对于每个点,要么属于这个组合,要么是不属于,所以复杂度为2^n, n最大为15, 再加上减枝, 时间足足矣。
#include<cstdio> #include<cstring> #define N 20 int n,m,vis[N], ans[N], pre[N], hash[N]; double G[N][N], weight[N], minCost[N], minRatio; double prim(){ int u; memset(hash,0,sizeof(hash)); for(int i=1;i<=n;i++){ if(vis[i]){ u=i; break; } } hash[u]=1; double weightsum=0,edgesum=0; for(int i=1;i<=n;i++) if(vis[i]){ minCost[i]=G[u][i]; pre[i]=u; weightsum+=weight[i]; } for(int i=1;i<m;i++){ u=-1; for(int j=1;j<=n;j++) if(vis[j]&&!hash[j]){ if(minCost[u]>minCost[j]||u==-1) u=j; } edgesum+=G[pre[u]][u]; hash[u]=1; for(int j=1;j<=n;j++) if(vis[j]&&!hash[j]){ if(minCost[j]>G[u][j]){ minCost[j]=G[u][j]; pre[j]=u; } } } return edgesum/weightsum; } void dfs(int u,int num){ if(num>m) return; if(u==n+1){ if(num!=m) return ; double t=prim(); if(t<minRatio){ minRatio=t; memcpy(ans,vis,sizeof(vis)); } return ; } vis[u]=1; dfs(u+1,num+1); vis[u]=0; dfs(u+1,num); } int main(){ while(~scanf("%d%d",&n,&m)){ if(m==0&&n==0) break; memset(G,0,sizeof(G)); memset(weight,0,sizeof(weight)); memset(vis,0,sizeof(vis)); for(int i=1; i<=n; ++i) scanf("%lf",&weight[i]); for(int i=1; i<=n; ++i) for(int j=1; j<=n; ++j) scanf("%lf",&G[i][j]); minRatio = 100000000; dfs(1, 0); bool flag=false; for(int i=1; i<=n; ++i)if(ans[i]){ if(flag) printf(" %d", i); else{ printf("%d",i); flag=true; } } puts(""); } return 0; }