CF-1099 D. Sum in the tree
题意:结点序号为 1~n 的一个有根树,根序号为1,每个点有一个权值a[i], 然后定义一s[i]表示从根节点到 结点序号为i的结点的路途上所经过的结点的权值之和。
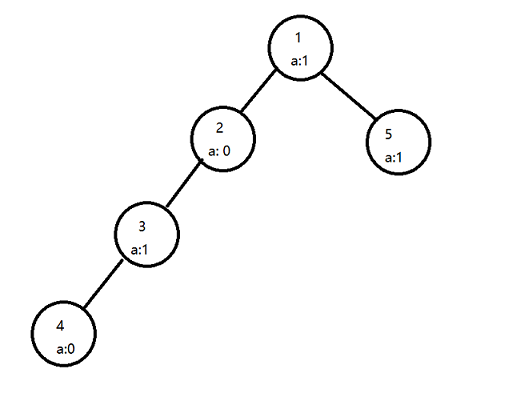
如图所示有:
s[1] = 1
s[2] = 2
s[3] = 2
s[4] = 2
s[5] = 2
而现在的情况是:所有的a我们都不知道,只知道部分的s,然后需要我们求出对a求和的最小值。
考虑一般情况,每一个结点有很多子结点。为了描述清楚,对于某个结点i,a为 i 的权值a[i],s为i的s[i]。
要使得a的和最小,那么对于每一个结点,就要求出最小权值。如果一个结点 i 有很多子结点,假设这些子结点中最小的s 为 min,那么我们可以让 a[i]=min ,使得结点 i 的权值对所有子结点的s有贡献,只有这样才能保证得到的答案是最小的。
经过上述的处理之后,对于现在还不清楚的点(s不知道的点),可以想到它们的权值为0也是同样可以满足的。所以直接将他们的权值赋值为0即可。
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll n,s[200005],p[200005],ans=0;
int main(){
cin>>n;
for(int i=2;i<=n;i++)
cin>>p[i];//p[i]为i的父节点
for(int i=1;i<=n;i++){
cin>>s[i];
if(s[i]==-1)s[i]=1e10;//标记为1e10是为了消除-1对我们得到min(分析中的min)的影响。
}
for(int i=1;i<=n;i++){
s[p[i]]=min(s[p[i]],s[i]);//每次对i的父节点的s进行更新,
}
for(int i=1;i<=n;i++){
if(s[p[i]]>s[i]){
cout<<-1;return 0;//如果父节点的s大于当前结点的s,则输出-1
}
if(s[i]==1e10)s[i]=s[p[i]];//如果s不清楚,则a[i]=0,s[i]=s[p[i]]
ans+=s[i]-s[p[i]];//如果s清楚,则a[i]=s[i]-s[p[i]];
}
cout<<ans<<endl;
return 0;
}