简单的线段树以及线段树数组四倍大小讨论

线段树

介绍

最基本的线段树拥有 单点更新(OlogN) 和 区间查询(OlogN) 的良好性质. 他的核心思想将一个区间不断地进行二分, 减少运算量.

基本思路

使用数组存储线段树中各个点的具体值, 若一个结点的下标为rt, 则他的左儿子下标为 rt << 1, 右儿子下标为 rt << 1 | 1.

查询操作

1. 若 当前区间 在所要 查询区间 内, 则 返回当前区间的值 , 结束递归.
2. 若 当前区间 拥有所要 查询区间 的值, 则 继续递归, 它的 子递归 会 自动 将有效区间和无效区间分离.
3. 若 当前区间 不在所要 查询区间 , 则 不执行任何操作 , 结束递归.

更新及建树操作

1. 递归找到相应区间.
2. 更新当前值.

关于数组大小

1. 首先线段树是一棵 full binary tree , 维基百科关于 full binary tree 的定义为

full binary tree (sometimes referred to as a proper or plane binary tree) is a tree in which every node in the tree has either 0 or 2 children.

2. 若一棵满二叉树的 叶子结点为 n , 则 非叶子结点个数为 n - 1 . 则 总的结点数为 2n - 1.

3. 那问题为 2n - 1 个结点的满二叉树, 需要的多大的数组进行存储?

   先来讨论 高度 h

   对于一棵 普通 的满二叉树 最坏的情况就是如图所示, n 个叶子结点, 共有 n 层, h = n

![](http://images2017.cnblogs.com/blog/976146/201710/976146-20171030205221371-1581836071.png)


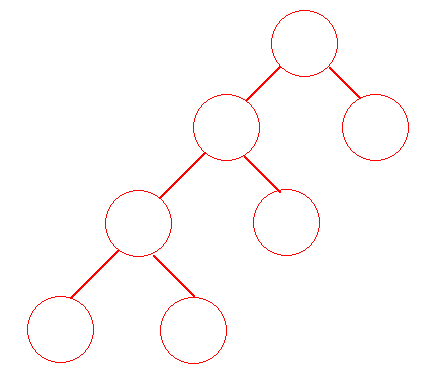
 当然这种情况肯定不可能发生, 因为, 我们每棵 **子树** 都是 **二分** 得出来的, 所以 **最多差一**.

 最好的情况

 ![](http://images2017.cnblogs.com/blog/976146/201710/976146-20171030205238480-295593878.png)

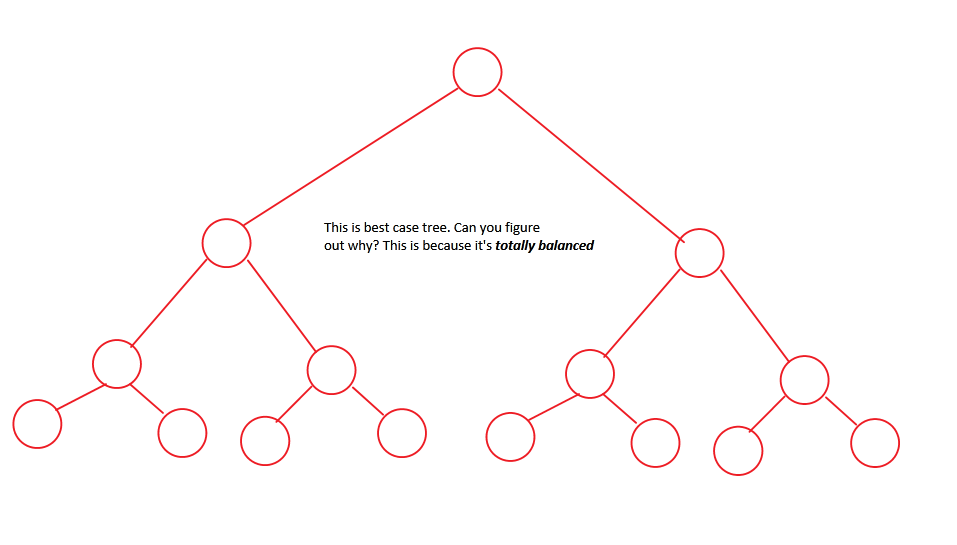
 *较差* 的情况

![](http://images2017.cnblogs.com/blog/976146/201710/976146-20171030205257324-1495461317.png)

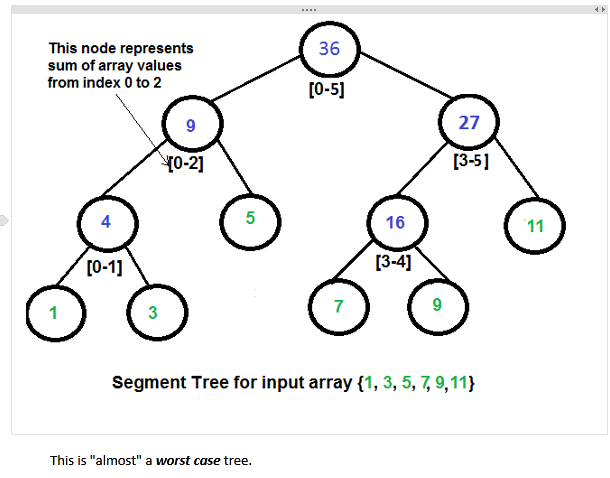
 所以对于一颗拥有 n 个叶子结点的线段树的高度 **h = ⌈ Log2n ⌉ + 1**

4. 既然知道了高度 h, 那么则总的结点数目为 2⌈ Log2n ⌉ + 1 -1
   也就是 2*2⌈ Log2n ⌉ -1.
   所以, 依照经验, 四倍的空间够了~

代码

#include <cstdio>
#include <algorithm>
#define lson l, m, rt << 1
#define rson m + 1, r, rt << 1 | 1
#define INF 999999
using namespace std;

const int maxn = 222222;
int MAX[maxn << 2];
int MIN[maxn << 2];
int SUM[maxn << 2];
int max(int a, int b){return a > b ? a : b;}
int min(int a, int b){return a < b ? a : b;}
void PushUP(int rt){
    MAX[rt] = max(MAX[rt << 1], MAX[rt << 1 | 1]);
    MIN[rt] = min(MIN[rt << 1], MIN[rt << 1 | 1]);
    SUM[rt] = SUM[rt << 1] + SUM[rt << 1 | 1];
}
void build(int l, int r, int rt){
    if(l == r){
        int val;
        scanf("%d", &val);
        MAX[rt] = MIN[rt] = SUM[rt] = val;
        return;
    }
    int m = (l + r) >> 1;
    build(lson);
    build(rson);
    PushUP(rt);
}
int queryMax(int L, int R, int l, int r, int rt){
    if(L <= l && r <= R)
        return MAX[rt];
    int m = (l + r) >> 1;
    int ret = -1;
    if(L <= m) ret = max(ret, queryMax(L, R, lson));
    if(R > m) ret = max(ret, queryMax(L, R, rson));
    return ret;
}
int queryMin(int L, int R, int l, int r, int rt){
    if(L <= l && r <= R)
        return MIN[rt];
    int m = (l + r) >> 1;
    int ret = INF;
    if(L <= m) ret = min(ret, queryMin(L, R, lson));
    if(m < R) ret = min(ret, queryMin(L, R, rson));
}
int querySum(int L, int R, int l, int r, int rt){
    if(L <= l && r <= R)
        return SUM[rt];
    int m = (l + r) >> 1;
    int sum = 0;
    if(L <= m) sum += querySum(L, R, lson);
    if(m < R) sum += querySum(L, R, rson);
}
void updateReplace(int loc, int val, int l, int r, int rt){
    if(loc == l && loc == r){
        SUM[rt] = MIN[rt] = MAX[rt] = val;
        return;
    }
    int m = (l + r) >> 1;
    if(loc <= m) updateReplace(loc, val, lson);
    else updateReplace(loc, val, rson);
    PushUP(rt);
}
void updateIncrease(int loc, int dert, int l, int r, int rt){
    if(loc == l && loc == r){
        SUM[rt] = MIN[rt] = MAX[rt] += dert;
        return;
    }
    int m = (l + r) >> 1;
    if(loc <= m) updateIncrease(loc, dert, lson);
    else updateIncrease(loc, dert, rson);
    PushUP(rt);
}
int main(){
    int n, m;
    scanf("%d%d
", &n, &m);
    build(1, n, 1);
    //区间最大A 区间最小B 区间求和C 单点替换D 单点增加E 单点减少F
    while(m--){
        char op[2];
        int a, b;
        scanf("%s%d%d", op, &a, &b);
        if(op[0] == 'A')
            printf("%d
", queryMax(a, b, 1, n, 1));
        else if(op[0] == 'B')
            printf("%d
", queryMin(a, b, 1, n, 1));
        else if(op[0] == 'C')
            printf("%d
", querySum(a, b, 1, n, 1));
        else if(op[0] == 'D')
            updateReplace(a, b, 1, n, 1);
        else if(op[0] == 'E')
            updateIncrease(a, b, 1, n, 1);
        else if(op[0] == 'F')
            updateIncrease(a, b, 1, -n, 1);
    }
}