2016 noip 复赛 day2

T1 组合数题目

 解：这题好像如果知道一个公式，应该就可以做了吧。。。

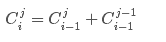
重点在于不知道。。。。。

程序：

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
using namespace std;
int a[20000],b[20000],c[2010][2010],f[2010][2010];
int t,k,n,m;
int main()
{
  scanf("%d%d",&t,&k);
  for (int i=1;i<=t;i++)
  {
      scanf("%d%d",&a[i],&b[i]);
      n=max(n,a[i]);
      m=max(m,b[i]);
  }
  for (int i=0;i<=2009;i++)
   for (int j=0;j<=2009;j++)
   c[i][j]=-1;
  for (int i=0;i<=n;i++) c[i][1]=i%k;
  for (int i=0;i<=n;i++) c[i][i]=1%k;
  for (int i=1;i<=n;i++)
   for (int j=2;j<=min(m,i);j++)
   if (i!=j)
       c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
  for (int i=1;i<=n;i++)
   for (int j=1;j<=m;j++)
   {
    f[i][j]=f[i-1][j]+f[i][j-1]-f[i-1][j-1];
    if (c[i][j]==0) f[i][j]++;
   }
  for (int i=1;i<=t;i++)
  if ((a[i]==0)||(b[i]==0)) printf("0
");
  else printf("%d
",f[a[i]][min(a[i],b[i])]); 
  return 0;

T2 蚯蚓 

  这题第一个想法就是用堆来储存，每次都挑出最大的那只，然后切，再放回去。为了解决每只蚯蚓每秒都会增长，放入堆的时候需减去总共已增长的长度，拿出的时候再加上，就解决了这个问题。但是这样写的话，我就只写了55分。。。。

  然后考虑就会发现，我们把当前的蚯蚓切成了t1和t2，因为蚯蚓每秒都在增长，所以保证t1一定大于下一次被切出的t1,t2一定大于下一次被切出的t2，只是我们不知道各个t1和t2间的大小关系罢了，那么我们就来维护三个队列，开始时，第一个队列为蚯蚓初始长度，并且由大到小排列，第二第三都为空，我们每次选取三个队首中最长的那条蚯蚓进行切分，并把得到的分开的两条蚯蚓分别放回第二和第三队列，反正第二个队列与第三个队列的单调性并不需要去维护就可以保持，这样就免除了之前每次都要logn维护，这样做m次操作。在最后把三个队列合并（切记，不能为了省事就把它们放一个数组里面后用快排，因为三个队列中都是各自有序的，这会导致快排退化，我就因为懒这么做了，然后。。。。还是老老实实两个两个合并吧），然后输出就好了。。

不过在洛谷上是对了，可是在bzoj上,是Presentation_Error，意思是答案基本正确，但有一些细节错误，总之就是一个多空格或者多空行的错误，然而我找不到我哪儿多了。。。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<algorithm>
using namespace std;
inline int read()
{
    char c;
    while((c<'0')||(c>'9')) c=getchar();
    int ef = 0;
    while((c>='0')&&(c<='9'))
    {
      ef=ef*10+c-48;
      c=getchar();
    }
    return ef;
}
int t1,t2,t3,n,m,l,t,x,sum,u,v,h1,h2,h3,tot;
long long ans;
int q1[8000001],q2[8000001],q3[8000001],b[8000001];
bool cmp(const int x,const int y) {return (x>y);}
void find1()
{
    int maxx=-2147438646;
    int tx=0;
    if ((q1[h1]>maxx)&&(h1<=t1)){maxx=q1[h1]; tx=1;}
    if ((q2[h2]>maxx)&&(h2<=t2)){maxx=q2[h2]; tx=2;}
    if ((q3[h3]>maxx)&&(h3<=t3)){maxx=q3[h3]; tx=3;}
    if (tx==1) h1++;
    else if (tx==2) h2++;
    else if (tx==3) h3++;
    ans=maxx;
}
int main()
{
  n=read();m=read();l=read();u=read();v=read();t=read();
  h1=h2=h3=1; 
  t1=n;t2=t3=0;
  for (int i=1;i<=n;i++) q1[i]=read();
  sort(q1+1,q1+n+1,cmp);
  sum=0;
  int now2,now,now1;
  tot=0;
  int tu=t;
  for (int i=1;i<=m;i++)
  {
      find1();
      ans=ans+tot;
      now=(int)(ans*u/v);
      tot+=l;
      if ((i==tu)&&(tu+t<=m)) {printf("%lld ",ans);tu+=t;}
      else if (i==tu) {printf("%lld",ans);tu+=t;}
      q2[++t2]=now-tot;
      q3[++t3]=ans-now-tot;
  }
  int sum=0;
  cout<<endl;
  tu=t;
  while ((h1<=t1)||(h2<=t2))
  {
      if ((h1<=t1)&&(h2<=t2))
      {
        sum++;
        if (q1[h1]>q2[h2]){b[sum]=q1[h1];h1++;}
        else {b[sum]=q2[h2];h2++;}
    }
    else 
    {
        sum++;
        if (h2<=t2) {b[sum]=q2[h2];h2++;}
        else {b[sum]=q1[h1];h1++;}
    }
  }
  for (int i=1;i<=sum;i++) q2[i]=b[i];
  h2=1;t2=sum;
  sum=0;
  while ((h3<=t3)||(h2<=t2))
  {
      if ((h3<=t3)&&(h2<=t2))
      {
        sum++;
        if (q3[h3]>q2[h2]){b[sum]=q3[h3];h3++;}
        else {b[sum]=q2[h2];h2++;}
    }
    else 
    {
        sum++;
        if (h2<=t2) {b[sum]=q2[h2];h2++;}
        else {b[sum]=q3[h3];h3++;}
    }
  }
  
  for (int i=1;i<=sum;i++) 
  if ((i==tu)&&(tu+t<=sum)) {printf("%d ",b[i]+tot);tu+=t;}
  else if (i==tu) {printf("%d",b[i]+tot);tu+=t;}
  return 0;
}

T3 愤怒的小鸟

原谅我在做这道题之前没有做过状态压缩dp,总之就是用f[i]来表示在i的二进制表达下，打掉那些表示为1的小猪最少需几只鸟，比如说i为5，即二进制为101是，f[5]表示的是打掉第一只猪和第三只猪最少需要几只鸟。

具体的一些解释就在程序里讲好了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
double x[30],y[30];
int t,n,m,f[300000],bird[20][20];
double eps=1e-9;
struct per{
    double a,b;
};
per calc(int i,int j)//这个纸上写写就好了。。。
{
  double x1=x[i],y1=y[i],x2=x[j],y2=y[j];
  per now;
  now.a=(y1*x2-y2*x1)/(x1*x1*x2-x2*x2*x1);
  now.b=(y1*x2*x2-y2*x1*x1)/(x1*x2*x2-x1*x1*x2);
  return now;
}
int check(double xx)//判等，因为==的精度太高。。。
{
  if (abs(xx)<=eps) return 0;
  else return 1;
}
int main()
{
  scanf("%d",&t);
  for (int pop=1;pop<=t;pop++)
  {
      scanf("%d%d",&n,&m);
      for (int i=1;i<=n;i++) scanf("%lf%lf",&x[i],&y[i]);
       //首先输入每只猪的坐标
      for (int i=0;i<=299999;i++) f[i]=2100000000;
      for (int i=1;i<=19;i++)
       for (int j=1;j<=19;j++)
       bird[i][j]=0;
//bird[i][j]表示同时经过（0,0）,（xi,yi）,(xj,yj)
//这三个点的二次函数能经过哪些点？首先如果存在这个函数的话，把这个数化为
二进制，它的第i位和第j位一定是1，表示它能经过这两个点，如果有一只猪（xk，yk）
也存在于这个二次函数上的话，那么这个数的第k位也就为1,不经过的话对应的位数就为零，
所以这个数表示的是经过这两点的函数能经过哪几只猪。
      for (int i=1;i<=n;i++)
       for (int j=i+1;j<=n;j++)
       {
         per sum=calc(i,j);
//计算同时经过（0,0）,（xi,yi）,(xj,yj)这个二次函数对应的a和b;
         if (sum.a>=0) continue;
//如果开口朝上就不存在抛物线了，所以除去
         for (int k=1;k<=n;k++)
         if (check(sum.a*x[k]*x[k]+sum.b*x[k]-y[k])==0)  bird[i][j]=bird[i][j]|(1<<(k-1));
//看看有哪些猪是位于这条函数上的，如果位于，就把对应的二进制位数变为零
     }
  f[0]=0;
  int tot=1<<n; 
  for (int i=0;i<=tot-1;i++)//枚举当前状态，即达到i的二进制这种情况下，至少需要几只小鸟。
   for (int j=1;j<=n;j++)
   if ((i&(1<<(j-1)))==0)//找到标号最前面的那只还未被打掉的小猪。
   {
        for(int k=j+1;k<=n;k++) 
//枚举它之后的还没被打掉的小猪
     {
       if ((i&(1<<(k-1)))==0)
       f[i|bird[j][k]]=min(f[i|bird[j][k]],f[i]+1);
//看看打掉这两只小猪以及与他们两位于同一抛物线上的小猪，和原来i枚举的那些小猪的最小步数能不能被更新
     }
     f[i|(1<<(j-1))]=min(f[i|(1<<(j-1))],f[i]+1);
//有可能只有j一个没被打掉，所以还要考虑这种情况 
     break;
//如果这个程序不加这个break，就会因超时失去三十分。。。
但很明显一眼看上去会认为这是不对的，因为它会少枚举很多的情况，
结果我们会发现j枚举的是i状态下编号最早的那只没被打的猪，你会发
现反正我们早晚都要消灭它，不如在最早的时候消灭好了，何必空着去
消灭后面的呢？（之后还是要回来消灭它）利用贪心原理，所以我们只
需找到第一个j就可以了，把第一只没被打的打掉。
   }
   printf("%d
",f[(1<<n)-1]);    
  }
  return 0;
}