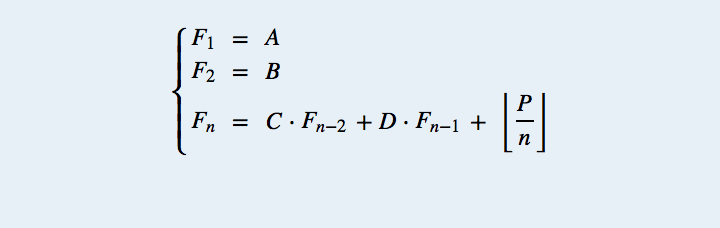hdu6395 （矩阵快速幂+分块）

 
Online Judge    Online Exercise    Online Teaching    Online Contests    Exercise Author
F.A.Q
Hand In Hand
Online Acmers    
Forum | Discuss
Statistical Charts
Problem Archive
Realtime Judge Status
Authors Ranklist
 
     C/C++/Java Exams     
ACM Steps
Go to Job
Contest LiveCast
ICPC@China
Best Coder beta
VIP | STD Contests
Virtual Contests 
    DIY | Web-DIY beta
Recent Contests
Author 2014＞
Mail Mail 0(0)
Control Panel Control Panel 
Sign Out Sign Out

2018百度之星复赛晋级名单出炉（增加20%晋级名额）~
Sequence

Time Limit: 4000/2000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)
Total Submission(s): 1365    Accepted Submission(s): 491


Problem Description
Let us define a sequence as below

  Your job is simple, for each task, you should output Fn module 109+7.
 

Input
The first line has only one integer T, indicates the number of tasks.

Then, for the next T lines, each line consists of 6 integers, A , B, C, D, P, n.

1≤T≤200≤A,B,C,D≤1091≤P,n≤109
 

Sample Input
2
3 3 2 1 3 5
3 2 2 2 1 4
 

Sample Output
36
24
 

Source
2018 Multi-University Training Contest 7
 

Recommend
chendu   |   We have carefully selected several similar problems for you:  6396 6395 6394 6393 6392 
 

 分块矩阵快速幂

构造    0 1  0            fn-2            fn-1

          c d  1     *       fn-1   =       fn

          0 0 1              p/i              p/i

 //这题也是利用这个性质，比如p=16,
//那么：i按照p/(p/i)+1来递增，
//得到：1，2，3，4，5，6，9，17.
//滑动的区间中每个数对于p来说除数一样，比如【9，17）这部分对于16来说除数都是1，

#include<iostream>
#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
#define ll long long
const int mod =1e9+7;
struct node{
    ll a[4][4];
};
struct pp{
    ll a[4][2];
};
ll num[1000000];
ll num2[100000];
node juzheng(node p,node q)
{
    node ans;
    memset (ans.a,0,sizeof ans.a);
    for(int i=1; i<=3; i++)
        for(int j=1; j<=3; j++)
            for(int h=1; h<=3; h++)
                ans.a[i][j] =(ans.a[i][j]+p.a[i][h]*q.a[h][j])%mod;
    
      return ans;
}
pp juzheng2(node z,pp q)
{
    pp ans;
    memset (ans.a,0,sizeof ans.a);
    ans.a[1][1]=(z.a[1][1]*q.a[1][1]+z.a[1][2]*q.a[2][1]+z.a[1][3]*q.a[3][1])%mod;
    ans.a[2][1] =(z.a[2][1]*q.a[1][1]+z.a[2][2]*q.a[2][1]+z.a[2][3]*q.a[3][1])%mod;
    ans.a[3][1] =(z.a[3][1]*q.a[1][1]+z.a[3][2]*q.a[2][1]+z.a[3][3]*q.a[3][1])%mod;
    return ans;
}

node juzheng_qsm(node q,int m)
{
    node ans;
    memset(ans.a,0,sizeof(ans.a));
    ans.a[1][1]=1;ans.a[2][2]=1;ans.a[3][3]=1;
  while(m)
  {
      if(m%2==1)
      {
          ans=juzheng(ans,q);
      }
      m=m/2;
      q=juzheng(q,q);
  }
    return ans;
}

int main()
{
    int n;
    scanf("%d",&n);
    while(n--)
    {
        ll A,B,C,D,p,n;
        memset(num2,0,sizeof num2);
        scanf("%lld%lld%lld%lld%lld%lld",&A,&B,&C,&D,&p,&n);
        if(n<=2) {printf("%lld
",n==1?:B);continue;}
        ll cnt=0;
        ll temp=-1;
       
        pp S;
        S.a[1][1]=A;
        S.a[2][1]=B;
        S.a[3][1]=0;
        node san;
        memset(san.a,0,sizeof san.a);
        san.a[1][2]=1;
        san.a[2][1]=C; san.a[2][2]=D; san.a[2][3]= san.a[3][3]=1;
        ll  L=min(p,n);
        ll i;
        for( i=3;i<=L;i=min(L,p/(p/i))+1)
        {
          S.a[3][1]=p/i;
          S=juzheng2(juzheng_qsm(san,min(n,p/(p/i))+1-i),S);
        }
      
        if(--i<n)
        {
            S.a[3][1]=0;
           S=juzheng2(juzheng_qsm(san,n-i),S);
        }
      
        cout<<S.a[2][1]<<endl;
        

    }
    return 0;
}