函数理论部分:
1.函数的定义:



2.函数的调用:
def Function(n) : # 计算阶乘 sum = 1 for i in range(1,n + 1) : sum *= i return sum print(Function(10))
3.函数的参数传递:

# 函数可以没有参数,但必须保留括号 # 函数定义时,可以为某些参数设置指定默认值,构成可选参数 def Function(n,m = 1) : # 计算阶乘 sum = 1 for i in range(1,n + 1) : sum *= i return sum // m print(Function(10,10)) # 362880

# 可变参数传递 def Function(n,*b) : # 计算阶乘 并乘以b中最大的数字 sum = 1 for i in range(1,n + 1) : sum *= i return sum * max(*b) print(Function(10,[1,2,3,4,5])) # 18144000

4.函数的返回值:
# return 可有、可无、可多传 def Function(n,m = 1) : sum = 1 for i in range(1,n + 1) : sum *= i return sum // m, n, m # 元组类型 print(Function(10,5)) # (725760, 10, 5)
5.局部变量、全局变量:

# global 保留字,本例中使全局变量在函数中使用 n , s = 10 , 10 def Function(n) : global s # 声明是全局变量s for i in range(1,n + 1) : s *= i return s print(Function(n),s) # 36288000 36288000
组合数据类型本用指针实现,故如上所示;
6.lambda函数:(有点迷,不知道咋搞。。。)
七段数码管绘制:
import turtle,time def DrawGap(): # 每条线之间的间隔--好看 turtle.penup() turtle.fd(5) def DrawLine(draw) : # 画一条线,可能在空中移过,可能在纸上画下 DrawGap() # 由draw参数确定 turtle.pendown() if draw else turtle.penup() turtle.fd(40) turtle.right(90) def DrawDigit(digit) : # 根据给出的时间字符串画出实际的线条 # 每个数字对应一系列特定的数码管号(a-g),根据数字来确定是否绘制该数码管 DrawLine(True) if digit in [2,3,4,5,6,8,9] else DrawLine(False) # g DrawLine(True) if digit in [0,1,3,4,5,6,7,8,9] else DrawLine(False) # c DrawLine(True) if digit in [0,2,3,5,6,8,9] else DrawLine(False) # d DrawLine(True) if digit in [0,2,6,8] else DrawLine(False) # e turtle.left(90) DrawLine(True) if digit in [0,4,5,6,8,9] else DrawLine(False) # f DrawLine(True) if digit in [0,2,3,5,6,7,8,9] else DrawLine(False) # a DrawLine(True) if digit in [0,1,2,3,4,7,8,9] else DrawLine(False) # b turtle.left(180) turtle.penup() turtle.fd(20) # 每个数字之间的间隔 def DrawDate(date) : turtle.pencolor("red") # 年--红色 for i in date : # 遍历时间字符串 if i == '-' : turtle.write("年",font = ("Arial",18,"normal")) turtle.pencolor("green") # 月--绿色 turtle.fd(40) elif i == '=' : turtle.write("月",font = ("Arial",18,"normal")) turtle.pencolor("blue") # 日--蓝色 turtle.fd(40) elif i == '+' : turtle.write("日",font = ("Arial",18,"normal")) else : DrawDigit(eval(i)) def main() : turtle.setup(800,350,200,200) turtle.penup() turtle.fd(-300) turtle.pensize(5) DrawDate(time.strftime("%Y-%m=%d+",time.gmtime())) turtle.hideturtle() # hide the turtle turtle.done() main()

函数应用部分(代码复用与函数递归):
1.代码复用与模块化设计:

2.函数递归:
# 字符串反转 s[::-1] def rvs(s) : if s == "" : return s else : return rvs(s[1:]) + s[0] print(rvs("Python")) # nohtyP # 斐波拉契数列 def f(n) : if n <= 2 : return 1 else : return f(n - 1) + f(n - 2) print(f(5)) # 5 # hanoi count = 0 def hanoi(n,src,dst,mid) : global count if n == 1 : print("{}:{}->{}".format(1,src,dst)) count += 1 else : hanoi(n - 1,src,mid,dst) print("{}:{}->{}".format(n,src,dst)) count += 1 hanoi(n - 1,mid,dst,src) hanoi(3,'A','C','B') print(count)
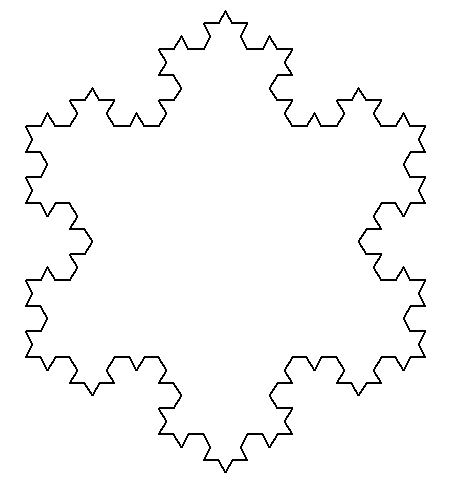
函数实例(科赫雪花):
import turtle def koch(size,n) : if n == 0 : turtle.fd(size) else : for angle in [0,60,-120,60] : turtle.left(angle) koch(size / 3,n - 1) def main() : turtle.setup(600,600) turtle.penup() turtle.goto(-200,100) turtle.pendown() turtle.pensize(2) level = 3 koch(400,level) turtle.right(120) koch(400,level) turtle.right(120) koch(400,level) turtle.hideturtle() turtle.done() main()
2021-01-25