入门级
引入
先看一道模板题洛谷P3374
题意是:维护一个序列,要求支持两种操作:
- 把元素(x)的值修改成(y)
- 查询区间([x,y])的和
依然可以用暴力,时间复杂度(O(N^2)),太慢了,出题人不会那么善意的让暴力过掉的
那么,我们需要优化到(O(N~log~N)),才能过
看过线段树的同学肯定一下看出来可以用线段树做,但是,线段树的常数比较大,
一些比较恶意的出题人依然会把它卡掉,所以我们需要常数更小的做法
而且代码量那么大,能用树状数组我才懒得打线段树
我们先不考虑修改操作,先考虑查询操作
因为我们查询的是和,我们就可以先预处理出前缀和,然后查询就会很方便
这时候我们再来考虑修改操作,正常更新前缀和的时间复杂度是(O(n))的
但是树状数组可以神奇地把它优化到(O(log~n)),代价是查询变成(O(log~n)),但比我们的暴力还是要优秀不少的
然后我们就要用到树状数组了
正题
1. lowbit函数
这个函数非常重要,它几乎贯彻整个树状数组
int lowbit(int x){
return x&(-x);
}
(lowbit(x)=2^{x在二进制下从右往左数第一个1的位置-1})
比如(5_{(10)}=101_{(2)})那么(lowbit(5)=1_{(2)}=1_{(10)})
(~~~~~~~6_{(10)}=110_{(2)})那么(lowbit(6)=10_{(2)}=2_{(10)})
2. 树状数组的结构
树状数组算是树型结构了,但在代码中是以数组的形式体现
大小为(8)树状数组长这个样子(红色的是边)

不难看出第(i)号节点的父亲是第(i+lowbit(i))号节点
树状数组的第(x个节点)表示的是(sumlimits_{i=x-lowbit(x)+1}^{x}a[i])
乍一看好像没什么用,还很复杂,事实上是非常好用的东西
3. 重点:原理
不把这里看懂的话,大概两天之后你就会忘掉到底要怎么写树状数组
树状数组利用了类似于倍增 大概是吧 的想法,结构神奇,但是非常巧妙
查询
假如我们要查询11~(7)的前缀和,那么我们需要的值就是(7)号节点的值、(6)号节点的值和(4)号节点的值
这些节点之间看起来没有什么关系 (~~)反正我第一次没看出什么关系~~,但是我们把它们转成二进制:
(7_{10}=111_{2})
(6_{10}=110_{2})
(4_{10}=100_{2})
(0_{10}=000_{2})
如果没看出关系的同学,可以再看下一组数据:
假如我们要查询(1)~(5)的前缀和,那么我们需要的值就是(5)号节点的值和(4)号节点的值
(5_{10}=101_{2})
(4_{10}=100_{2})
(0_{10}=000_{2})
可以再举一个例子:
假如我们要查询(1)~(45)的前缀和,那么我们需要的值就是(45)号节点的值、(44)号节点的值
(45_{10}=101101_{2})
(44_{10}=101100_{2})
(40_{10}=101000_{2})
(32_{10}=100000_{2})
(0_{10}=00000_{2})
规律就出来了:下一个所查找的数的下标=这个数的下标-(lowbit()这个数的下标())
简单来说就是把现在的数的下标在二进制中的最后一个(1)变成(0),直到这个数为0为止
这就和我们树状数组的结构很有关系了:
树状数组的第(x个节点)表示的是(sumlimits_{i=x-lowbit(x)+1}^{x}a[i])
这样统计前缀和的方式是非常巧妙的,因为我们如果有(n)个元素,那么它最多有(lceil log_2n ceil)个1,则时间复杂度是(O(log~N))的
修改
当我们要修改一个值的时候,我们还要把它影响的值全部修改
假如我们要把第(7)号的节点的值加上(x),那么编号为(7)、(8)的节点的值均要加上(x)
同样是换成二进制:
(7_{10}=0111_{2})
(8_{10}=1000_{2})
再来两个例子:
假如我们要把第(5)号的节点的值加上(x),那么编号为(5)、(6)、(8)的节点的值均要加上(x)
(5_{10}=0101_{2})
(6_{10}=0110_{2})
(8_{10}=1000_{2})
假如我们要把第(45)号的节点的值加上(x),那么编号为(7)、(8)的节点的值均要加上(x)
(45_{10}=0101101_{2})
(46_{10}=0101110_{2})
(48_{10}=0110000_{2})
(64_{10}=1000000_{2})
规律是:下一个所修改的数的下标=这个数的下标+(lowbit()这个数的下标())
同样,时间复杂度是(O(log~N))
4. 树状数组的查询(代码)
树状数组不支持任意区间查询,只支持查询前缀
但是查询到前缀后,我们就可以得出答案
巧妙的使用(lowbit)函数
时间复杂度(O(log~N))
void get_sum(int x){//查询1到x的和
int re=0;
while(x){
re=re+sum[x];
x=x-lowbit(x);
}
}
5. 树状数组的修改(代码)
树状数组不支持区间修改,只支持单点修改
要修改一个点的值之后,还需要把它到根的路径上的点进行维护
时间复杂度(O(log~N))
void update(int x,int y){//把第x个元素加y
while(x<=n){
sum[x]=sum[x]+y;
x=x+lowbit(x);
}
}
6. 模板题代码
于是我们就把模板题做出来了:
#include<bits/stdc++.h>
using namespace std;
const int MAXN=500001;
int n,m,x,y,t,sum[MAXN];
int lowbit(int x){
return x&(-x);
}
void update(int x,int y){//把第x个元素加y
while(x<=n){
sum[x]=sum[x]+y;
x=x+lowbit(x);
}
}
int get_sum(int x){//查询1到x的和
int re=0;
while(x){
re=re+sum[x];
x=x-lowbit(x);
}
return re;
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&x);
update(i,x);
}
while(m--){
scanf("%d",&t);
if(t==1){
scanf("%d%d",&x,&y);
update(x,y);
}else{
scanf("%d%d",&x,&y);
printf("%d
",get_sum(y)-get_sum(x-1));
}
}
}
提高级
先看一道模板题洛谷P3368
题意是:
维护一个长度为(n)的区间,要求支持两个操作
- 把区间([l,r])之间的值加上(x)
- 输出第(x)号节点的值
分析
很明显出题人不会那么善意的让暴力过掉,(n,mle 500000)的大数据让我们必须要拿出(O(log~N))或更优的算法
那么我们又怎么和树状数组扯上关系呢
我们知道树状数组只可以解决有关于前缀的问题
那么我们考虑把区间修改操作换成两个修改后缀的操作
也就是,我们可以把区间([l,r])的值加上(x)的操作改成([l,n])加上(x),([r+1,n])加上(-x)
那么我们就可以很容易用树状数组操作了
上代码
#include<bits/stdc++.h>
using namespace std;
const int MAXN=5000002;
int n,m,l,r,t,x,sum[MAXN];
int lowbit(int x){return x&(-x);}
void update(int x,int y){while(x<=n){sum[x]=sum[x]+y;x=x+lowbit(x);}}
int get_sum(int x){int re=0;while(x){re=re+sum[x];x=x-lowbit(x);}return re;}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&x);
update(i,x);update(i+1,-x);
}
while(m--){
scanf("%d",&t);
if(t==1){
scanf("%d%d%d",&l,&r,&x);
update(l,x);update(r+1,-x);
}else{
scanf("%d",&x);
printf("%d
",get_sum(x));
}
}
}
再补充一种神奇的用法:
翻译后:
在卡卡的家门前有一棵苹果树,每个秋天都会结许多苹果。卡卡非常喜欢苹果,所以他总是悉心照料这棵大苹果树。
这棵树有n个分叉点,并且它们之间有树枝连接。卡卡将这些分叉点编号,并且树根的编号总是1。苹果就长在这些分叉点上,当然一个分叉点不会长出两个及以上的苹果。卡卡想要知道一棵子树中有多少苹果,以此来了解这棵苹果树的生产能力。
现在的麻烦是,有些时候,卡卡会从树上摘下苹果,而有些时候,一个没有苹果的分叉点上又会长出苹果。你能帮卡卡处理这个问题吗?
Input
输入文件第一行是一个正整数n(1<=n<=100000),代表苹果树的分叉点数。
接下来n-1行,每行两个整数u和v,代表分叉点u和v之间有一根树枝相连。
第n行包含一个正整数m(1<=m<=100000),代表操作的数目。
接下来m行,每行代表一个操作。操作可以是以下两种之一:
(1)“C x”代表在分叉点x上的苹果状态被改变了。也就是说,如果之前分叉点x上有苹果,那么现在就被摘掉了;反之,如果以前没有苹果,那么现在就长出了一个苹果。
(2)“Q x”代表查询以分叉点x为根的子树中一共有多少苹果(包括x上的苹果,如果分叉点上x上有苹果的话)
一开始,树上长满了苹果。
Output
对每个查询,输出一行一个整数,代表该子树上的苹果个数。
Sample Input
3
1 2
1 3
3
Q 1
C 2
Q 1
Sample Output
3
2
题解:
先想一下暴力算法,一共有两种:
- 更改直接更改节点的值,查询时遍历整颗子树,更改(O(1)),查询(O(N)),可以卡掉
- 更改时遍历更改节点的所有祖先,查询就可以做到(O(1)),但是修改可以卡到(O(N))(当树退化成链),照样卡掉
那么我们可以将查询的时间复杂度与修改的时间复杂度均衡一下,都变成(O(log N)),就可以过了
下面才是正题:
我们考虑把树用dfn序表示
(这里是对dfn序的介绍,了解过的同学可以跳过)
dfn序就是我们在对树进行遍历时的遍历出来的序列,顺序是先遍历根,后遍历子树,类似于二叉树的先序遍历,但我们现在所讨论的遍历是对于多叉树的
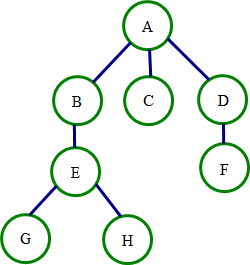
比如我们对下面的树进行遍历时,dfn序就是ABEGHCDF
不难看出dfn序的一个性质:一个节点的后代在dfn序中是相邻的
写一下遍历的代码:
void dfs(int now){//有根树的遍历,无根树在遍历时要加上到父亲的特判 dfn[++cnt]=now;//cnt是时间戳,dfn数组里存的是dfn序 in[now]=cnt;//in数组存的是now的子树在dfn序中对应的序列的开头的下标 for(int i=head[now];~i;i=nxt[i])dfs(child[now]);//对儿子进行遍历 out[now]=cnt;//out数组存的是now的子树在dfn序中对应的序列的末尾的下标 }
我们可以巧妙领dfn序的性质,把树表示成一维的,同时使用查分的思想,把答案统计转换成前缀和的统计
然后就可以用树状数组处理这一题了,查询和修改的时间复杂度都是(O(log N))
上面可能讲的不够清楚,不懂得同学可以对照代码理解一下
#include<iostream>
using namespace std;
int n,x,y,q,cnt,a[1000001],in[1000001],out[1000001],v[1000001],nxt[1000001],head[1000001];
bool tf[1000001];//tf数组储存第i号节点有没有苹果
char st[2];
void add_edge(int x,int y){//加双向边
v[++cnt]=x;nxt[cnt]=head[y];head[y]=cnt;
v[++cnt]=y;nxt[cnt]=head[x];head[x]=cnt;
}
int low_bit(int x){
return x&(-x);
}
void add(int x,int y){//树状数组更新
while(x<=n){
a[x]=a[x]+y;
x=x+low_bit(x);
}
}
int sum(int x){//树状数组求和
int ans=0;
while(x>0){
ans=ans+a[x];
x=x-low_bit(x);
}
return ans;
}
int ans(int x,int y){//查分
return sum(y)-sum(x-1);
}
void dfs(int now,int la){//处理出dfn序
in[now]=++cnt;
for(int i=head[now];i!=0;i=nxt[i])if(v[i]!=la)dfs(v[i],now);
out[now]=cnt;
}
int main(){
scanf("%d",&n);
for(int i=1;i<n;i++){
scanf("%d%d",&x,&y);
add_edge(x,y);
}
cnt=0;
dfs(1,-1);//dfn序
for(int i=1;i<=n;i++)add(i,1),tf[i]=true;//一开始树的每个节点都有苹果
scanf("%d",&q);
for(int i=1;i<=q;i++){
scanf("%s%d",st,&x);
if(st[0]=='Q')printf("%d
",ans(in[x],out[x]));else{
if(tf[in[x]])add(in[x],-1);//有苹果就摘掉
else add(in[x],1);//没苹果就长出来
tf[in[x]]=!tf[in[x]];
}
}
}
小结:
树状数组的基本知识到这里就差不多讲完了,实际应用很广,不可能一篇博客写完,遇到可以查分的问题可以向查分想想,大概就是这样了