返回整数数组最大子数组和2
为了实现“敏捷开发”的目的,老师让我们采取“迭代”的方法进行项目的开发,这不,对于周一的求最大子数组和又有了新的要求,如下:
1、延续上次的要求,这里不再赘余…
2、如果数组A[0]……A[j-1]首尾相连,允许A[i-1],……A[n-1],A[0]……A[j-1]之和最大;
3、同时返回最大子数组的位置;
4、要求程序必须能处理1000 个元素,且每个元素是int32 类型的。
一、实验设计思路
首先实现的是数组首尾相连,先存入数组,再将原数组反向存储形成环形数组。接着求最大子数组的和,遍历数组里面的每一个数将第一个数变成为最后一个数,形成一个新的数组,计算数组中每个最大子数组的和存入另一个数组max[]中,并记录最大子数组位置,最后找max[]数组中最大值为所求。
二、实验源代码
1 //返回整数数组最大子数组和2 2 //孔宇航 赵子茵 2016/3/25 3 4 #include <iostream> 5 using namespace std; 6 #define N 1000 7 8 int value(int arry[], int length) 9 { 10 int max[N], max1; 11 int maxweizhi[N]; 12 for (int j = 0; j<(length + 1) / 2; j++) 13 { 14 int sum = 0; 15 max1 = -9999999; //设置最低范围 16 int z = 0; 17 for (int i = j; i<(length + 1) / 2 + j; i++) //环形数组找最大子数组和 18 { 19 sum = sum + arry[i]; 20 if (sum >= max1) 21 { 22 max1 = sum; 23 z++; 24 } 25 } 26 max[j] = max1; 27 maxweizhi[j] = z; 28 29 } 30 int fmax = max[0]; 31 int q = 0; 32 for (int i = 0; i<(length + 1 / 2); i++) //在所有和的数组中找最大值 33 { 34 if (max[i]>fmax) 35 { 36 fmax = max[i]; 37 q = i; 38 } 39 } 40 41 int weizhi = maxweizhi[q]; 42 43 cout << "最大子数组为:" << endl; 44 for (int num = q; num<q + weizhi; num++) //输出最大子数组的位置 45 { 46 cout << arry[num] << " "; 47 } 48 49 cout << "其和为: " << fmax << endl; 50 return 0; 51 } 52 53 void main(int argc, char* argv[]) 54 { 55 int arry[N]; 56 int length = 1; 57 int max[N], max1; //max[N]存每一次求和的结果,在其中找最大值,为所求 58 int maxweizhi[N]; 59 int num = 0; 60 int value(int arry[], int length); 61 cout << "请输入数组:" << endl; 62 cin >> arry[0]; 63 while (getchar() != ' ') //输入数组 64 { 65 cin >> arry[length]; 66 length++; 67 } 68 69 for (int j = length; j<2 * length - 1; j++) //形成环形数组,首位相连 70 { 71 arry[j] = arry[num]; 72 num++; 73 } 74 75 cout << "由这几个数形成的环形数组"; 76 value(arry, 2 * length - 1); 77 78 }
实验截图如下:


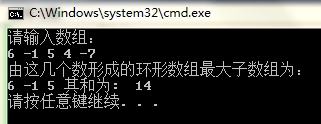
三、实验心得体会
通过这几次的结对开发,让我了解到软件开发过程中无论是结对还是团队合作都会比一个人的效率提高好多。我们都不是那种所谓的“抱大腿”的人,所以在团队中我们可以互相学习别人的好的思想来充实自己,因此还是有点期待以后的团队合作。
本次实验中对于怎样实现数组的“首尾相连”我和孔同学分别想到了很多的想法,其中也有几个想法被我们写成了可执行的文件,包括:扩展二倍数组、动态规划、定义开始和结束位置等方法,但是当考虑到还要输出最大子数组的位置的时候我们只在这个思想上面加上了这个功能。虽然有很多次尝试最后都失败了,但是我们要学会享受这个乐趣不是么?!哈!