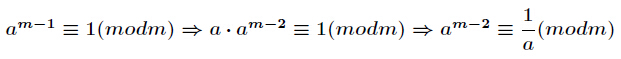A/B
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=1576
题目:
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 9278 Accepted Submission(s): 7452
Problem Description
要求(A/B)%9973,但由于A很大,我们只给出n(n=A%9973)(我们给定的A必能被B整除,且gcd(B,9973) = 1)。
Input
数据的第一行是一个T,表示有T组数据。
每组数据有两个数n(0 <= n < 9973)和B(1 <= B <= 10^9)。Output
对应每组数据输出(A/B)%9973。
Sample Input
2
1000 53
87 123456789
Sample Output
7922
6060
思路:
逆元: (a / b)% m 设c是b的逆元则 (a / b)% m = (a * c)% m
费马小定理:对于素数m 有gcd(b.m)=1,那么 b^(m-2) (mod m) = 1
(a / b)% m中 m为素数且 gcd(b , m)=1 (即b不是m的倍数) 则 c = b ^ (m-2) (mod m) ——用快速幂求
推导过程如下(摘自Acdreamer博客)
题目中 要求(A/B)%9973,但由于A很大,我们只给出n(n=A%9973)(我们给定的A必能被B整除,且gcd(B,9973) = 1)。
所以可用费马小定理求 b mod m 的逆元 c = b ^ (m-2) (mod m)
(a / b) % m = (a * c) % m = ( (a % m) * (c % m) ) % m
题目给出 n = (a % m) 所以 (a / b) % m = ( n * (c % m) ) % m
这题因为数据范围太大在用快速幂求 b%m 的逆元的时候 要一直取模
AC代码:
#include <stdio.h> #include <math.h> #include <iostream> using namespace std; typedef long long ll; ll poww(ll a,ll b); ll mod = 9973; int main() { // freopen("in.txt","r",stdin); ll t,n,b,c; scanf("%lld",&t); while(t--) { scanf("%lld %lld",&n,&b); c=poww(b,mod-2) % mod; cout<< (n*(c%mod))% mod <<endl; } return 0; } ll poww(ll a,ll b) { ll ans=1,base = (a%mod); while(b!=0) { if(b&1!=0) ans = ans*base%mod; base = base*base%mod; b>>=1; } return ans; }