CF1096E The Top Scorer

http://codeforces.com/problemset/problem/1096/E

题意：

一场游戏有p人参加，得分总和为s分，每个人的分数都是非负整数，且其中一号玩家的得分至少为r

而现在不知道具体的得分情况，求一号玩家获胜的概率，我们认为任何一种合法的得分情况出现的概率相等

得分最高的玩家获胜，特殊的，若有多人得分相同，他们获胜的几率相同

1≤p≤100，0≤r≤s≤5000，要求答案对998244353取模

---

这题考试的时候连暴力都没想出来555

看题解后，感觉到了一种套路。。。

设 g(s,p,m)=（在一场总分和s，玩家数p的游戏中，没有人得分超过m的合法状态数）

这东西dp起来蛮简单（的吧？），但是你会发现他的复杂度有点难以接受。。。但这至少给我们一个启示？

• 遇到获胜等设计随机状态中涉及最大值的问题，可以试着转化成一些“不超过”问题的组合

我们试着用数学方法解决这个问题吧

 

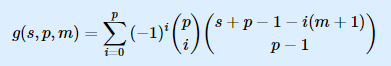
这个 这个公式出自隔板法和容斥原理，请允许我解释一下

首先看容斥，简单来说就是想计算 所有情况-至少一个人超过m+至少两个人超过m-至少三个人超过m……

然后看隔板法，如何计算有i个人超过m呢？先选出i个人C(p,i)，给每个人先分配m+1个，就变成了箱子内剩余数可以为零的经典隔板问题

这个式子在有预处理的帮助下的代价是O(p)的

有了g之后呢，答案f貌似就很好计算了，搬个公式大家自己体会吧~

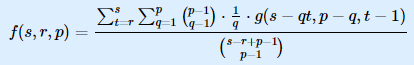
总复杂度：O(s*p²)

#include<cstdio>
#define ll long long
#define mod 998244353
using namespace std;
ll ksm(ll x,ll t){ll ans=1;for(;t;t>>=1,x=(x*x)%mod)if(t&1)ans=(ans*x)%mod;return ans;}
int p,s,r;
ll fac[6005],invf[6005];
void pre(){
    fac[0]=1;
    for(int i=1;i<=p+s;i++)fac[i]=(fac[i-1]*i)%mod;
    invf[p+s]=ksm(fac[p+s],mod-2);
    for(int i=p+s-1;i>=0;i--)invf[i]=(invf[i+1]*(i+1))%mod;
}
ll C(ll n,ll m){
    if(n<0||m<0||m>n)return 0;
    return ((fac[n]*invf[n-m])%mod*invf[m])%mod;
}
ll ans;
ll g(ll s,ll p,ll m){
    if(p==0&&s==0)return 1;
    ll tot=0;
    for(int i=0,t=1;i<=p;i++){
        tot+=t*(C(p,i)*C(s+p-1-i*(m+1),p-1)%mod);
        tot=(tot+mod)%mod;
        t*=-1;
    }
    return tot;
}
int main(){
    scanf("%d%d%d",&p,&s,&r);
    pre();
    for(int t=r;t<=s;t++)
    for(int q=1;q<=p;q++){
        ans+=((C(p-1,q-1)*ksm(q,mod-2)%mod)*g(s-q*t,p-q,t-1))%mod;
        ans%=mod;
    }
    ans*=ksm(C(s+p-1-r,p-1),mod-2);
    ans%=mod;
    printf("%lld",ans);
    return 0;
}