P2522 [HAOI2011]Problem b（莫比乌斯反演）

题目链接

题意：

 思路：首先由容斥定理可得

 

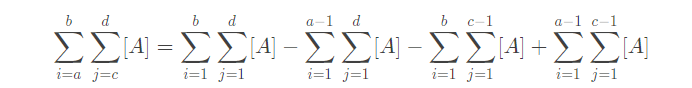
 红色箭头为反演步骤。

最后由数论分块来写。

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 50000;
int mu[N + 5], p[N + 5];
bool flg[N + 5];
void init() {
  int tot = 0;
  mu[1] = 1;
  for (int i = 2; i <= N; ++i) {
    if (!flg[i]) {
      p[++tot] = i;
      mu[i] = -1;
    }
    for (int j = 1; j <= tot && i * p[j] <= N; ++j) {
      flg[i * p[j]] = 1;
      if (i % p[j] == 0) {
        mu[i * p[j]] = 0;
        break;
      }
      mu[i * p[j]] = -mu[i];
    }
  }
  for (int i = 1; i <= N; ++i) mu[i] += mu[i - 1];
}
int solve(int n, int m) {
  int res = 0;
  for (int i = 1, j; i <=min(n, m); i = j + 1) {
    j=min(n / (n / i), m / (m / i));
    res += (mu[j] - mu[i - 1]) * (n / i) * (m / i);
  }
  return res;
}
int main() {
  int T, a, b, c, d, k;
  init();
  for (scanf("%d", &T); T; --T) {
    scanf("%d%d%d%d%d", &a, &b, &c, &d, &k);
    printf("%d
", solve(b / k, d / k) - solve(b / k, (c - 1) / k) -solve((a - 1) / k, d / k) +solve((a - 1) / k, (c - 1) / k));
  }
  return 0;
}