扫描线 hdu1542

扫描线分类两种，一种离散y轴，一种离散x轴。以离垂直x轴的直线为例：

将每个离散的线之间作为一个线段树的叶子节点，然后从最小与x轴平行的直线开始，区覆盖线段树的叶子节点，

也就是两根与y轴平行的直线之间所夹的空间，这段空间的长度乘以你的扫描线之间的距离（与x轴平行的直线），就是面积，

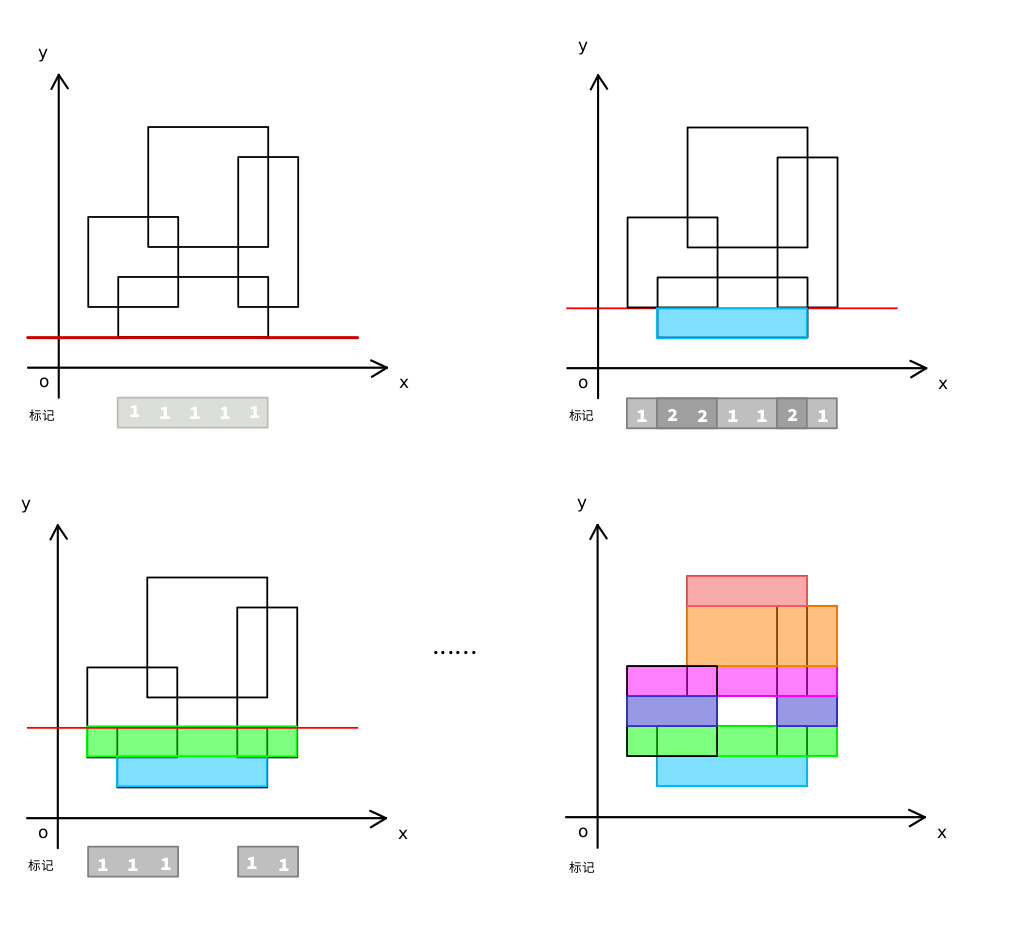
看图吧，图下的数字是代表覆盖的次数，矩形的下底线扫描覆盖节点时为 value +=1，上边线扫描 value -= 1；

代码如下

#include <map>
#include <cstring>
#include <cstdio>
#include <algorithm>
#include <map>

using namespace std;

const int maxn = 205;

struct node
{
    int r, l, lazy;
    double dat;
}tr[maxn<<2];

struct bian
{
    double x, a, b;
    int k;
}egde[maxn<<1];

int n;
double yy[maxn << 1];
map<double, int> mp;

//注意节点为 l+1=r，离散化会丢失离散节点之间的信息
void build(int p, int l, int r)
{
    tr[p].dat = 0;
    tr[p].l = l;tr[p].r = r;
    tr[p].lazy = 0;
    if (l == r - 1)return;
    int mid = (l + r) >> 1;
    build(p << 1, l, mid);
    build(p << 1 | 1, mid, r);
}

inline void push(int p)
{
    if (tr[p].lazy)tr[p].dat = yy[tr[p].r] - yy[tr[p].l];
    else if (tr[p].l + 1 == tr[p].r)tr[p].dat = 0;
    else tr[p].dat = tr[p << 1].dat + tr[p << 1 | 1].dat;
}

void updata(int p, int l, int r, int k)
{
    if (tr[p].l > r || tr[p].r < l) return;
    if (l <= tr[p].l && tr[p].r <= r)
    {
        tr[p].lazy += k;
        push(p);
        return;
    }
    int mid = (tr[p].l + tr[p].r) >> 1;
    if (l <= mid) updata(p << 1, l, r, k);
    if (mid < r) updata(p << 1 | 1, l, r, k);
    push(p);
}

bool cmp(const bian& a, const bian& b)
{
    if(a.x != b.x)return a.x < b.x;
    return a.k > b.k;
}

int main(void)
{
    /*freopen("atlantis.in", "r", stdin);
    freopen("atlantis.out", "w", stdout);*/
    for (int cas = 1;~scanf("%d", &n)&&n; ++cas)
    {
        double ans = 0;
        for (int i = 0; i < n; ++i)
        {
            double x, y, a, b;
            scanf("%lf%lf%lf%lf", &x, &y, &a, &b);
            egde[i << 1] = { x, y, b, 1 };
            egde[i << 1 | 1] = { a, y, b, -1 };
            yy[i << 1] = y;yy[i << 1 | 1] = b;
        }
        sort(yy, yy + (n << 1));sort(egde, egde + (n << 1), cmp);
        int tot = unique(yy, yy + (n << 1)) - yy;
        for (int i = 0; i < tot; ++i)mp[yy[i]] = i;
        build(1, 0, tot - 1);
        updata(1, mp[egde[0].a], mp[egde[0].b], egde[0].k);
        for (int i = 1; i < (n << 1); ++i)
        {
            ans += (egde[i].x - egde[i - 1].x) * tr[1].dat;
            updata(1, mp[egde[i].a], mp[egde[i].b], egde[i].k);
        }
        printf("Test case #%d
Total explored area: %.2lf

", cas, ans);
    }
    return 0;
}