图总结

一、思维导图

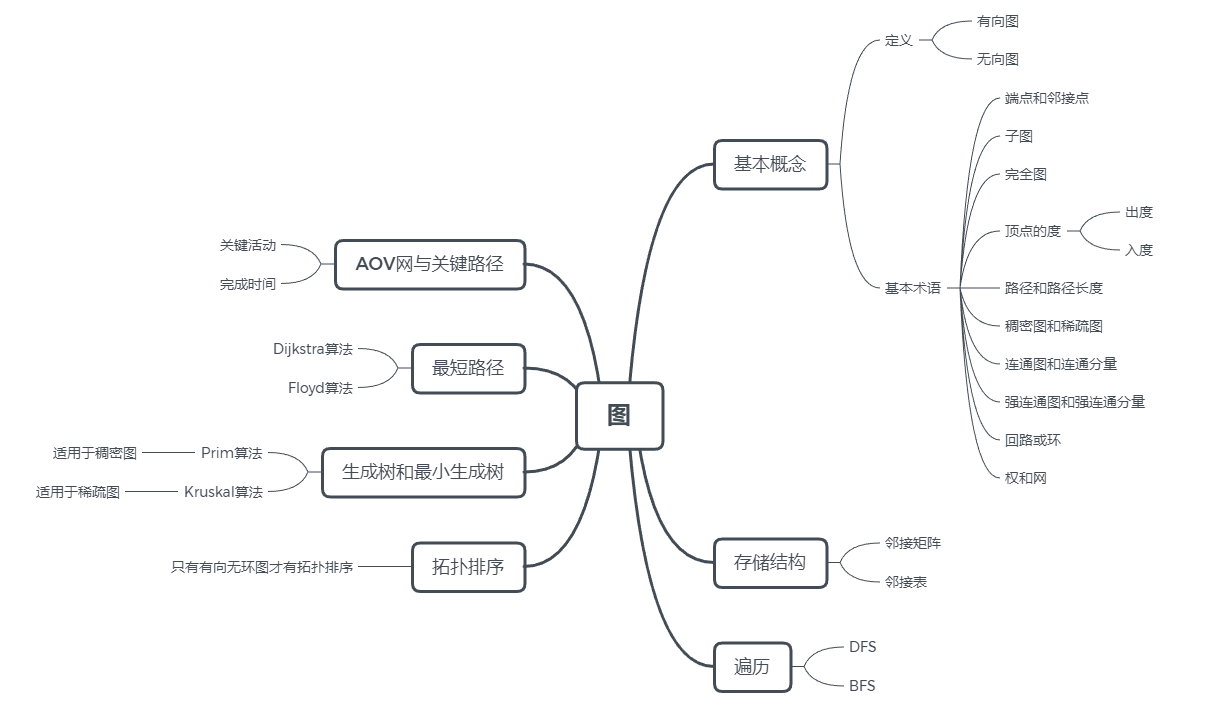
二、概念笔记

1、邻接表的DFS

void DFS(AdjGraph* G, int v) {
	for (int i = 1; i <= G->n; i++) visited[i] = 0;
	ArcNode* p;
	printf("%d ", v);
	visited[v] = 1;
	p = G->adjlist[v].firstarc;
	while (p != NULL) {
		if (visited[p->adjvex] == 0) {
			DFS(G, p->adjvex);
		}
		p = p->nextarc;
	}
}

2、邻接表的BFS

void BFS_AL(ALGraph &G, char v){	
    int u,w,v0;	
    ArcNode *p;	
    printf("%c ", v);		                                        	
    v = LocateVex(G, v);	                                                	
    visited[v0] = 1;			                                        	
    q.push(v);				                                	
    while (!q.empty())	
    {		
        u = q.front();		                                        		
        v0 = LocateVex(G, u);                                            		
        q.pop();					
        for (p = G.vertices[v0].firstarc; p; p = p->nextarc)				
        {			
            w = p->adjvex;				
            if (!visited[w])				
            {				
                printf("%c ", G.vertices[w].data);	        				
                visited[w] = 1;				       			
                q.push(G.vertices[w].data);						
            }		
        }	
    }
}

3、最小生成树

Kruskal算法

Kruskal算法在找最小生成树结点之前，需要对所有权重边做从小到大排序。将排序好的权重边依次加入到最小生成树中，如果加入时产生回路就跳过这条边，加入下一条边。当所有结点都加入到最小生成树中之后，就找出了最小生成树。

Prim算法

Prim算法首先以一个结点作为最小生成树的初始结点，然后以迭代的方式找出与最小生成树中各结点权重最小边，并加入到最小生成树中。加入之后如果产生回路则跳过这条边，选择下一个结点。直至所有结点都加入到最小生成树中。

4、最短路径

Dijkstra算法

Dijkstra算法算是贪心思想实现的，首先把起点到所有点的距离存下来找个最短的，然后松弛一次再找出最短的，所谓的松弛操作就是，遍历一遍看通过刚刚找到的距离最短的点作为中转站会不会更近，如果更近了就更新距离，这样把所有的点找遍之后就存下了起点到其他所有点的最短距离。

Floyd算法

Floyd算法是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法,算法目标是寻找从点i到点j的最短路径。
从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，算法假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，算法检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

三、疑难问题

Dijkstra算法和Floyd算法的实现(代码来自网络摘抄)

void Dijkstra(MGraph g,int v)
{
	int dist[MAXV],path[MAXV];
	int s[MAXV];
	int mindis,i,j,u;
	for (i=0;i<g.n;i++) 
	{	
		dist[i]=g.edges[v][i];
		s[i]=0;
		if (g.edges[v][i]<INF)
			path[i]=v;
		else
		    path[i]=-1;
	}
	s[v]=1;path[v]=0;
	for (i=0;i<g.n;i++)
	{	
		mindis=INF;
		for (j=0;j<g.n;j++)
			if (s[j]==0 && dist[j]<mindis) 
			{ 	
				u=j;
				mindis=dist[j];	
			}
		s[u]=1;
		for (j=0;j<g.n;j++)
			if (s[j]==0) 
				if (g.edges[u][j]<INF && dist[u]+g.edges[u][j]<dist[j]) 
				{	
					dist[j]=dist[u]+g.edges[u][j];
					path[j]=u;
				}  
	}
	Dispath(dist,path,s,g.n,v);
}
void Floyd(MGraph g)
{
 　　int A[MAXV][MAXV];
 　　int path[MAXV][MAXV];
 　　int i,j,k,n=g.n;
 　　for(i=0;i<n;i++)
    　　for(j=0;j<n;j++)
    　　{ 　　
             A[i][j]=g.edges[i][j];
         　　 path[i][j]=-1;
     　 }
 　　for(k=0;k<n;k++)
 　　{ 
      　　for(i=0;i<n;i++)
         　　for(j=0;j<n;j++)
             　　if(A[i][j]>(A[i][k]+A[k][j]))
             　　{
                   　　A[i][j]=A[i][k]+A[k][j];
                   　　path[i][j]=k;
              　 } 
    　} 
}