zoukankan      html  css  js  c++  java

  • 结对项目——四则运算题目生成器

    一、Github项目地址：https://github.com/3Jax/Arithmetic.git

    　　项目成员：纪昂学 3118005053 冷沐阳 3118005054

    二、PSP表格：在程序各个模块的开发上估计耗费的时间

    PSP2.1

    Personal Software Process Stages

    预估耗时（分钟）

    实际耗时（分钟）

    Planning

    计划

     60

    · Estimate

    · 估计这个任务需要多少时间

     60

    Development

    开发

     2960

    · Analysis

    · 需求分析 (包括学习新技术)

     800

    · Design Spec

    · 生成设计文档

     120

    · Design Review

    · 设计复审 (和同事审核设计文档)

     60

    · Coding Standard

    · 代码规范 (为目前的开发制定合适的规范)

     60

    · Design

    · 具体设计

     240

    · Coding

    · 具体编码

     1000

    · Code Review

    · 代码复审

     200

    · Test

    · 测试（自我测试，修改代码，提交修改）

     480

    Reporting

    报告

     360

    · Test Report

    · 测试报告

     180

    · Size Measurement

    · 计算工作量

     120

    · Postmortem & Process Improvement Plan

    · 事后总结, 并提出过程改进计划

     60

    合计

     3380

    三、效能分析

    　　生成1w道数值为50的题目（依次执行功能）后的效能如下：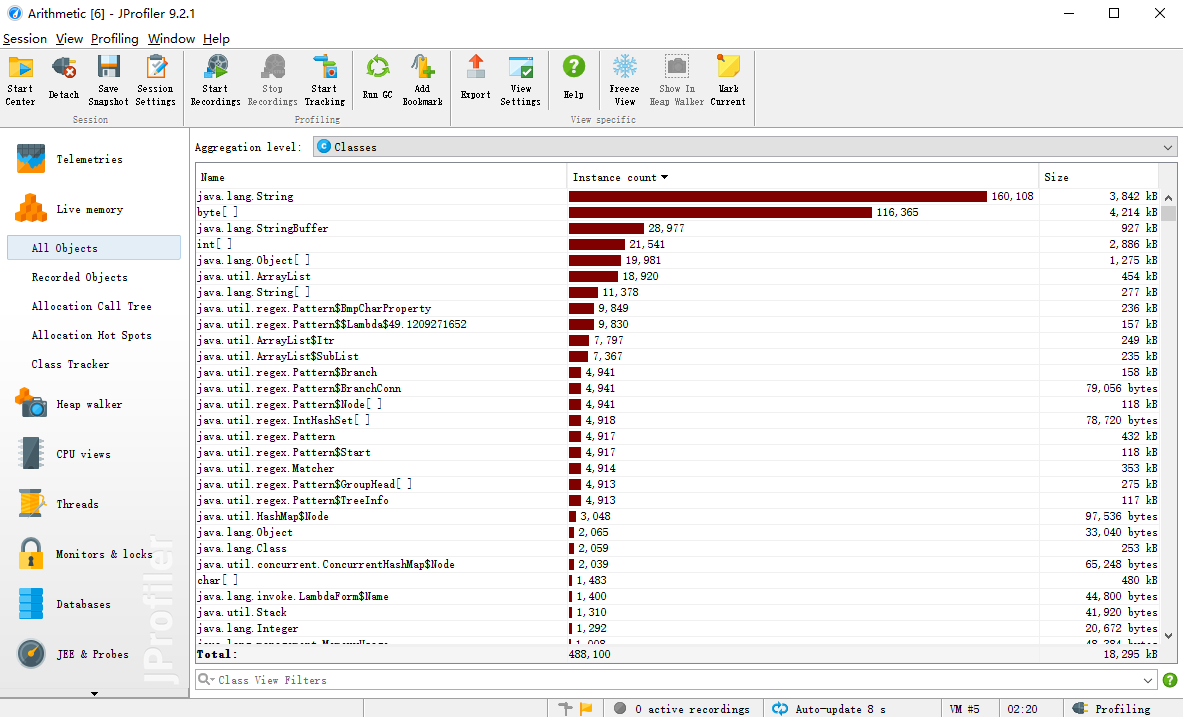

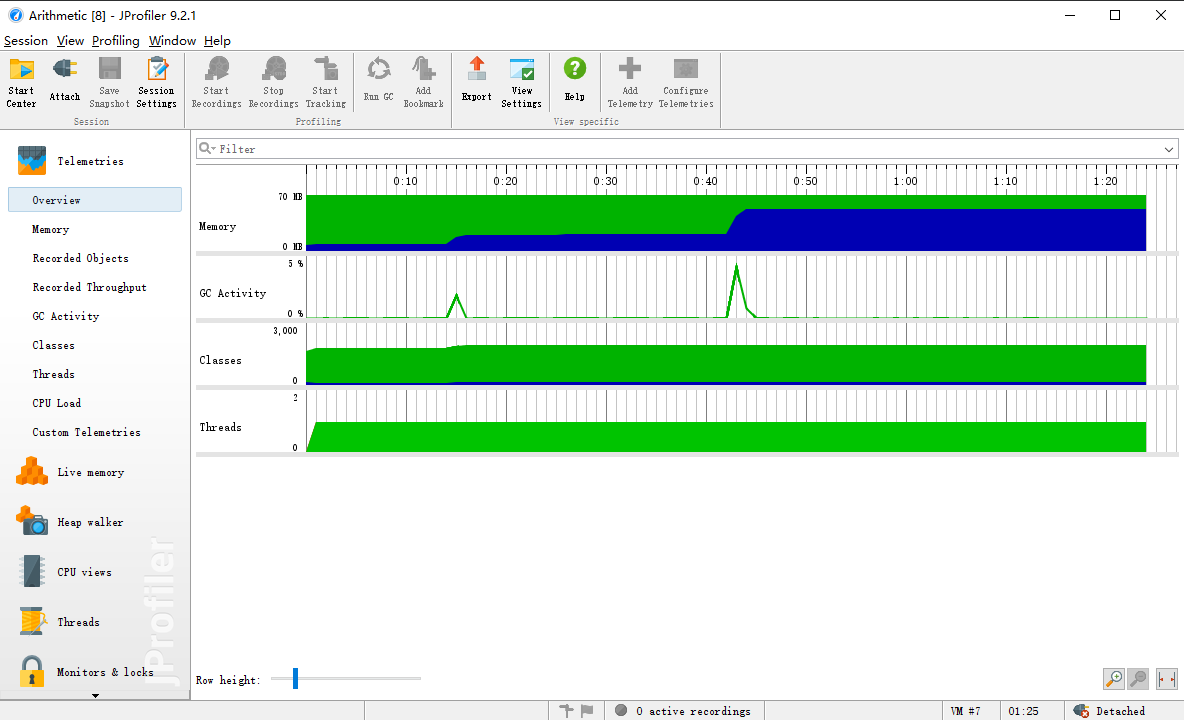
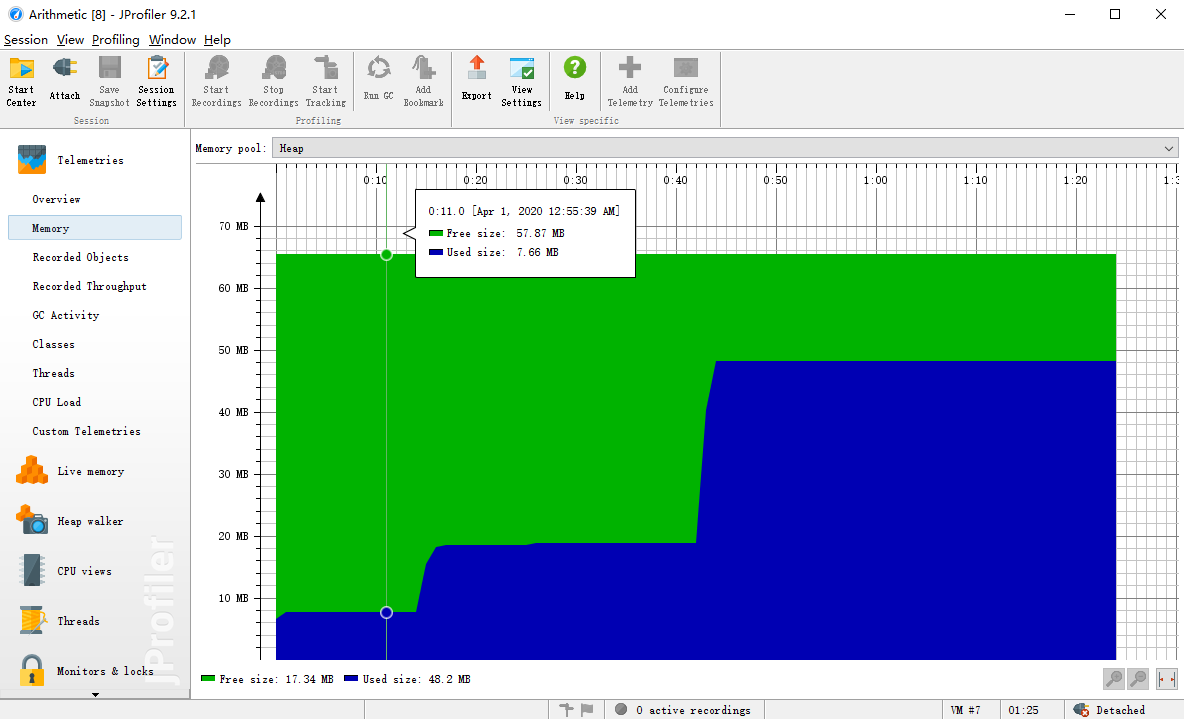
    四、设计实现过程

    　　1.本项目一共使用了六个类，功能如下表所示：

    类名 类的功能说明
    Arithmetic 生成功能列表，调用其他类以实现四则运算功能
    Create 根据用户输入的题数n和数值范围r生成题目和答案（Exercise.txt和Answers.txt）
    Answers 输入题目返回答案（均为StringBuffer类型）
    Fuction 实现真分式加、减、乘和除的功能（add()、sub()、mul()、div()）
    Txt 实现.txt文件的写入与读取（write()写入、read()读取）
    User 提供用户输入答案的函数和校对用户答案的函数（inPutAnswers()、result()）

    　　2.各个类相互关系如下图所示：

    　　 

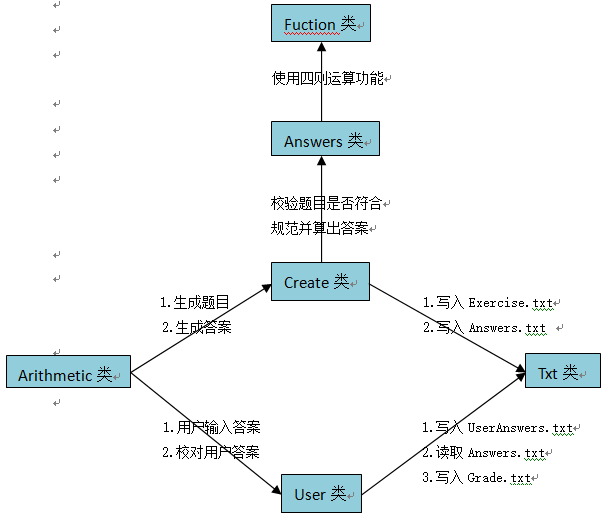
    　　3.关键函数思路：

    　　　　1）实现功能的关键函数是Answers类的answer()函数，其功能为：传入一个StringBuffer类型的四则运算表达式(含括号、真分式)，返回一个StringBuffer类型的答案(使用真分式表示)

    　　　　设计过程为：传入StringBuffer类型的题目——>ArrayList<StringBuffer>类型的题目——>ArrayList<StringBuffer>类型的逆波兰式——>计算StringBuffer类型的答案

    　　　　a)StringBuffer类型的题目，无法区别数字、运算符和括号，故无法直接对其进行计算，需要提取出StringBuffer类型的数字、运算符和括号，用一个容器ArrayList<StringBuffer>存储起来。具体为定义一个字符数组t存储前缀表达式的字符，对其遍历，遇到运算符、括号和数字的首位就新建StringBuffer对象来存储，遇到其余位置的数字则加入原有的StringBuffer对象，区分是否为数字的首位只需设置一个标志位tag判断。

    　　　　b)计算机无法直接区分出四则运算表达式(含括号)的运算顺序，故还需要对分离出数字，运算符和括号的中缀表达式进行处理，变成计算机能够处理的形式，即将中缀表达式转换为逆波兰式/后缀表达式。具体为定义一个栈s和ArrayList<StringBuffer>类型的后缀表达式，遍历ArrayList<StringBuffer>类型的前缀表达式，若遇到数字则直接新建一个StringBuffer对象加入到后缀表达式中；若遇到左括号则直接入栈；若遇到右括号则将栈顶元素依次出栈并新建一个StringBuffer对象加入到后缀表达式，直到遇到左括号(左右括号不必加入后缀表达式)；若遇到加减乘除则将高于该运算符优先级的运算符依次出栈并新建一个StringBuffer对象加入到后缀表达式，直到栈顶元素的优先级低于该运算符，接着将该运算符入栈。遍历结束后将栈中的运算符依次出栈加入后缀表达式

    　　　　c)后缀表达式中隐含着表达式的运算顺序，根据其能计算出表达式结果。具体为将后缀表达式遍历，若遇到数字内容的StringBuffer对象则入栈；若遇到运算符内容StringBuffer对象则取出栈中的两个数字对象，然后进行相应运算操作(调用Fuction函数)，并将结果存入栈。遍历结束后，栈中的唯一对象即为结果。

    　　　　2）实现功能的关键函数二是Fuction类的add()/sub()/mul()/div()函数，其功能为：传入一个StringBuffer类型的只含一个加/减/乘/除的表达式，返回一个StringBuffer类型的答案(使用真分式表示)

    　　　　设计过程为：考虑到运算数包括真分数，运用判断语句判断运算数类型过于繁琐，效能低。故在设计加/减/乘/除功能时默认都用分式的运算方法来计算，最终算出结果后再判断是否为整数，并做相应的转换。具体为先用辗转相除法求写出求最大公约数和最小公倍数的函数(gcd()/lcm()函数)，然后在加/减/乘/除函数中调用，进行通分约分，即可得到分数形式的答案，简单处理即可得到真分数或整数类型答案。(PS：0无最大公约数和最小公倍数，需要单独处理)

    五、代码说明

    　　1.根据用户输入的题数n和数值范围r生成题目和答案

     1 package cn.homework;
 2 /**
 3  * 创建类，根据用户输入的题数n和数值范围r生成题目和答案
 4  */
 5 
 6 import java.util.ArrayList;
 7 import java.util.List;
 8 import java.util.Random;
 9 
10 public class Create {
11     public static final char[] ch={'+','-','*','/'};  //ch数组存放四个运算符
12 
13     public static void getQuestionsAndAnswers(int n,int r) {
14         Random random = new Random();  //生成一个随机数生成器
15         List<StringBuffer> listQuestions = new ArrayList<StringBuffer>();  //listQuestions存放题目（StringBuffer）
16         List<StringBuffer> listAnswers = new ArrayList<StringBuffer>();  //listQuestions存放题目（StringBuffer）
17         StringBuffer t;  //temp用于拼接StringBuffer
18         int num,c,chNum,kuoNum;
19 
20         //生成n条式子
21         for (int i = 0; i < n; i++) {
22             chNum = random.nextInt(3) + 1;  //chNum为第i条式子的运算符数
23             t = new StringBuffer();
24             t.append(random.nextInt(r));  //输入第一个随机数（每条式子的随机数的数目比运算符多1）
25             for (int j = 0; j < chNum; j++) {  //再随机生成chNum个运算符和随机数
26                 c=random.nextInt(4);
27                 num=random.nextInt(r);
28                 if(c==3&&num==0){  //除数不能为0
29                     j--;
30                     continue;
31                 }
32                 t.append(ch[c]);  //拼接一个运算符
33                 t.append(num);  //拼接一个0~r的随机数
34             }
35             kuoNum=1;//可用随机数更改产生括号概率random.nextInt(2);
36             char[] temp=t.toString().toCharArray();
37             int j; //加减号位置
38             for(j=0;j<temp.length;j++){
39                 if(kuoNum==1&&(temp[j]=='-'||temp[j]=='+')){
40                     break;
41                 }
42             }
43             int a=0,b=j+2;//其前后两个数的位置
44             if (j == temp.length) {
45             }else{  //在加减号前后插入括号
46                 for(int k=0;k<j;k++){
47                     if(temp[k]<'0'||temp[k]>'9'){
48                         a=k+1;
49                     }
50                 }
51                 for(int k=j+2;k<temp.length;k++){
52                     if(temp[k]>='0'&&temp[k]<='9'){
53                         b++;
54                     }else{
55                         break;
56                     }
57                 }
58                 if(a!=0&&t.toString().charAt(a-1)!='/') {  //保证除数不为0且括号不在首个数字生成
59                     t.insert(a, '(');
60                     t.insert((b + 1), ')');
61                 }
62             }
63             if(Answers.getAnswers(t).toString().charAt(0)=='-'){  //生成的式子的答案若为负数，则重新生成
64                 i--;
65                 continue;
66             }
67             listQuestions.add(t);  //生成的表达式加入到list中
68         }
69         //System.out.println(listQuestions); 测试时使用
70         for(StringBuffer b: listQuestions){
71             listAnswers.add(Answers.getAnswers(b));
72             //System.out.print(Answers.getAnswers(b)+", "); 测试时使用
73         }
74 
75         //把问题写入文本文件
76         Txt.write(listQuestions,"E:/Exercises.txt");
77         //把答案写入文本文件
78         Txt.write(listAnswers,"E:/Answers.txt");
79 
80         //弹出Exercises.txt
81         try {
82             Process process = Runtime.getRuntime().exec("cmd.exe  /c notepad e:/Exercises.txt");
83         } catch (Exception e) {
84             e.printStackTrace();
85         }
86     }
87 }

    　　2.输入题目返回答案（均为StringBuffer类型）

      1 package cn.homework;
  2 /**
  3  * 答案类，输入题目返回答案（均为StringBuffer类型）
  4  */
  5 
  6 import java.util.ArrayList;
  7 import java.util.List;
  8 import java.util.Stack;
  9 
 10 public class Answers {
 11     //求一条表达式（StringBuffer）的答案（StringBuffer）
 12     //思路:传入StringBuffer类型的题目——>ArrayList<StringBuffer>类型的题目——>ArrayList<StringBuffer>类型的逆波兰式——>计算StringBuffer类型的答案
 13     public static StringBuffer getAnswers(StringBuffer infix) {
 14         Stack<StringBuffer> s = new Stack<StringBuffer>();
 15         char[] t=infix.toString().toCharArray();//t用于保存中缀表达式的字符
 16         int tag=0;  //tag用于在处理字符串时标志之前的字符是否为数字。0：不是，1：是
 17         List<StringBuffer> temp= new ArrayList<StringBuffer>();  //临时存放处理后的中缀表达式（infix）
 18         List<StringBuffer> suffix=new ArrayList<StringBuffer>(); //逆波兰式
 19 
 20         //处理存储在temp中字符串（操作数与运算符分离）
 21         for (char c : t) {
 22             if (c >= '0' && c <= '9') {  //为0~9的数字
 23                 if (tag == 0) {
 24                     temp.add(new StringBuffer(c + ""));  //注意StringBuffer构造方法需要转换为字符串
 25                     tag = 1;
 26                 } else {
 27                     temp.get(temp.size() - 1).append(c);
 28                 }
 29             } else {  //为（）或运算符
 30                 tag = 0;
 31                 temp.add(new StringBuffer(c + ""));  //注意StringBuffer构造方法需要转换为字符串
 32             }
 33         }
 34         //System.out.println("处理前缀表达式字符串:"+temp); 测试专用
 35 
 36         //由中缀表达式infix得到逆波兰式suffix
 37         for (StringBuffer b : temp) {
 38             if (b.toString().equals("(")) {  //c为左括号直接入栈（优先级最低）
 39                 s.push(b);
 40             } else if (b.toString().equals(")")) {
 41                 while (!s.peek().toString().equals("(")) {  //栈非空且栈顶元素非'('则栈顶元素出栈拼接到后缀表达式
 42                     suffix.add(s.pop());
 43                 }
 44                 s.pop();
 45             } else if (b.toString().equals("+") || b.toString().equals("-")) {
 46                 while (!s.empty()) {
 47                     if (!s.peek().toString().equals("(")) {  //栈顶元素优先级高则出栈拼接到后缀表达式
 48                         suffix.add(s.pop());
 49                     } else {
 50                         break;
 51                     }
 52                 }
 53                 s.push(b);
 54             } else if (b.toString().equals("*") || b.toString().equals("/")) {
 55                 while (!s.empty()) {
 56                     if (s.peek().toString().equals("*") || s.peek().toString().equals("/")) {  //栈顶元素优先级高则出栈拼接到后缀表达式
 57                         suffix.add(s.pop());
 58                     } else {
 59                         break;
 60                     }
 61                 }
 62                 s.push(b);
 63             } else {  //c为数字,直接拼接到后缀表达式
 64                 suffix.add(b);
 65             }
 66         }
 67         while (!s.empty()) {  //将栈中剩余的运算符拼接到suffix
 68             suffix.add(s.pop());
 69         }
 70         //System.out.println("逆波兰式为:"+suffix); 测试专用
 71 
 72         //由逆波兰式计算结果（可继续使用栈s,再求逆波兰式时已被清空）
 73         //从左到右遍历表达式，遇到是数字就进栈，遇到符号就将处于栈顶两个数字出栈进行运算，运算结果进栈。
 74         StringBuffer t1,t2;  //a,b为两个操作数
 75         StringBuffer result;  //result为运算结果
 76         for(StringBuffer b : suffix){
 77             if(b.toString().equals("+")) {
 78                 t1 = s.pop(); //提取栈顶前两个操作数
 79                 t2 = s.pop();
 80                 result=Fuction.add(t2,t1);
 81                 s.push(result);  //将计算结果入栈
 82             }else if(b.toString().equals("-")){
 83                 t1 = s.pop(); //提取栈顶前两个操作数
 84                 t2 = s.pop();
 85                 result=Fuction.sub(t2,t1);
 86                 s.push(result);  //将计算结果入栈
 87             }else if(b.toString().equals("*")){
 88                 t1 = s.pop(); //提取栈顶前两个操作数
 89                 t2 = s.pop();
 90                 result=Fuction.mul(t2,t1);
 91                 s.push(result);  //将计算结果入栈
 92             }else if(b.toString().equals("/")){
 93                 t1 = s.pop(); //提取栈顶前两个操作数
 94                 t2 = s.pop();
 95                 result=Fuction.div(t2,t1);
 96                 s.push(result);  //将计算结果入栈
 97             } else{
 98                 s.push(b);
 99             }
100         }
101 
102         //返回的分式做简单处理
103         String[] str=s.peek().toString().split("/");
104         if(str.length==1){ //非分式，直接返回
105             return s.peek();
106         }else{  //分式，需要处理
107             int FenZi=Integer.valueOf(str[0]);  //分子和分母
108             int FenMu=Integer.valueOf(str[1]);
109             if(FenMu==1){  //若分母为1，返回分子
110                 return new StringBuffer(str[0]);
111             }else if(Math.abs(FenZi)<FenMu){
112                 return s.peek();
113             }else{  //若分子绝对值大于分母(分母不为1)，返回时化为真分数
114                 int r=FenZi/FenMu;; //真数
115                 FenZi = FenZi%FenMu;
116                 return new StringBuffer(r + "'" + FenZi + "/" + FenMu);
117             }
118         }
119     }
120 }

    　　3.实现真分式加、减、乘和除的功能

      1 package cn.homework;
  2 
  3 /**
  4  * 功能类，实现真分式加、减、乘和除的功能
  5  */
  6 public class Fuction {
  7     public static StringBuffer add(StringBuffer t1,StringBuffer t2){
  8         if(t1.toString().equals("0")){ //0没有最大公约数和最小公倍数，需要对0进行单独处理
  9             return t2;
 10         }
 11         if(t2.toString().equals("0")){
 12             return t1;
 13         }
 14         int temp;
 15         //将t1,t2化为分式
 16         StringBuffer a=fen(t1);
 17         StringBuffer b=fen(t2);
 18         //分离t1,t2的分子和分母
 19         String[] fen1=a.toString().split("/");
 20         String[] fen2=b.toString().split("/");
 21         //求t1,t2分母的最小公倍数（相加后的分母）
 22         int fenMuLcm=lcm(Integer.valueOf(fen1[1]),Integer.valueOf(fen2[1]));
 23         //求相加后的分子
 24         int fenZi=fenMuLcm/Integer.valueOf(fen1[1])*Integer.valueOf(fen1[0])+fenMuLcm/Integer.valueOf(fen2[1])*Integer.valueOf(fen2[0]);
 25         //约分
 26         if((temp=gcd(fenMuLcm,fenZi))!=1){
 27             fenMuLcm/=temp;
 28             fenZi/=temp;
 29         }
 30         //统一格式，分式为零则负号写在分子处,分子分母不同时有负号
 31         if(fenMuLcm<0){
 32             fenMuLcm=-fenMuLcm;
 33             fenZi=-fenZi;
 34         }
 35         return new StringBuffer(fenZi+"/"+fenMuLcm);
 36     }
 37     
 38     public static StringBuffer sub(StringBuffer t1,StringBuffer t2){
 39         if(t1.toString().equals("0")){ //0没有最大公约数和最小公倍数，需要对0进行单独处理
 40             return new StringBuffer("-"+t2.toString());
 41         }
 42         if(t2.toString().equals("0")){
 43             return t1;
 44         }
 45         int temp;
 46         //将t1,t2化为分式
 47         StringBuffer a=fen(t1);
 48         StringBuffer b=fen(t2);
 49         //分离t1,t2的分子和分母
 50         String[] fen1=a.toString().split("/");
 51         String[] fen2=b.toString().split("/");
 52         //求t1,t2分母的最小公倍数（相加后的分母）
 53         int fenMuLcm=lcm(Integer.valueOf(fen1[1]),Integer.valueOf(fen2[1]));
 54         //求相减后的分子
 55         int fenZi=fenMuLcm/Integer.valueOf(fen1[1])*Integer.valueOf(fen1[0])-fenMuLcm/Integer.valueOf(fen2[1])*Integer.valueOf(fen2[0]);
 56         //约分
 57         if((temp=gcd(fenMuLcm,fenZi))!=1){
 58             fenMuLcm/=temp;
 59             fenZi/=temp;
 60         }
 61         //统一格式，分式为零则负号写在分子处,分子分母不同时有负号
 62         if(fenMuLcm<0){
 63             fenMuLcm=-fenMuLcm;
 64             fenZi=-fenZi;
 65         }
 66         return new StringBuffer(fenZi+"/"+fenMuLcm);
 67     }
 68     
 69     public static StringBuffer mul(StringBuffer t1,StringBuffer t2){
 70         if(t1.toString().equals("0")||t2.toString().equals("0")) { //0没有最大公约数和最小公倍数，需要对0进行单独处理
 71             return new StringBuffer("0");
 72         }
 73         int temp;
 74         //将t1,t2化为分式
 75         StringBuffer a=fen(t1);
 76         StringBuffer b=fen(t2);
 77         //分离t1,t2的分子和分母
 78         String[] fen1=a.toString().split("/");
 79         String[] fen2=b.toString().split("/");
 80         //求相乘后的分母
 81         int fenMu=Integer.valueOf(fen1[1])*Integer.valueOf(fen2[1]);
 82         //求相乘后的分子
 83         int fenZi=Integer.valueOf(fen1[0])*Integer.valueOf(fen2[0]);
 84         //约分
 85         if((temp=gcd(fenMu,fenZi))!=1){
 86             fenMu/=temp;
 87             fenZi/=temp;
 88         }
 89         //统一格式，分式为零则负号写在分子处,分子分母不同时有负号
 90         if(fenMu<0){
 91             fenMu=-fenMu;
 92             fenZi=-fenZi;
 93         }
 94         return new StringBuffer(fenZi+"/"+fenMu);
 95     }
 96     
 97     public static StringBuffer div(StringBuffer t1,StringBuffer t2){
 98         if(t1.toString().equals("0")){ //0没有最大公约数和最小公倍数，需要对0进行单独处理
 99             return t1;
100         }
101         int temp;
102         //将t1,t2化为分式
103         StringBuffer a=fen(t1);
104         StringBuffer b=fen(t2);
105         //分离t1,t2的分子和分母
106         String[] fen1=a.toString().split("/");
107         String[] fen2=b.toString().split("/");
108         //求相除后的分母
109         int fenMu=Integer.valueOf(fen1[1])*Integer.valueOf(fen2[0]);
110         //求相乘后的分子
111         int fenZi=Integer.valueOf(fen1[0])*Integer.valueOf(fen2[1]);
112         //约分
113         if((temp=gcd(fenMu,fenZi))!=1){
114             fenMu/=temp;
115             fenZi/=temp;
116         }
117         //统一格式，分式为零则负号写在分子处,分子分母不同时有负号
118         if(fenMu<0){
119             fenMu=-fenMu;
120             fenZi=-fenZi;
121         }
122         return new StringBuffer(fenZi+"/"+fenMu);
123     }
124 
125     //将真分式化为纯分式
126     public static StringBuffer fen(StringBuffer t){
127         String[] temp=t.toString().split("'|/");
128         if(temp.length==1){ //为整数，分母为1
129             return t.append("/1");
130         }else if(temp.length==2) { //无'的分式，无需处理直接返回t
131             return t;
132         }else{
133             int fz,fm;
134             fm=Integer.valueOf(temp[2]);
135             fz=Integer.valueOf(temp[0])*fm+Integer.valueOf(temp[1]);
136             return new StringBuffer(fz+"/"+fm);
137         }
138     }
139 
140     //辗转相除法求最大公约数gcd
141     public static int gcd(int m,int n){
142         if(m==0||n==0) return 1;
143         int r;  //余数
144         if(m<n){  //保证m>n
145             r=m;
146             m=n;
147             n=r;
148         }
149         while (m%n!=0){
150             r=m%n;
151             m=n;
152             n=r;
153         }
154         return n;
155     }
156 
157     //求最小公倍数lcm
158     public static int lcm(int m,int n){
159         return m*n/gcd(m,n);
160     }
161 }

    六、测试运行

    　　1. 菜单如下：

    　　

    　　2. 运行功能1：弹出Exercise.txt(方便用户输入答案)；不弹出Answers.txt

    　　

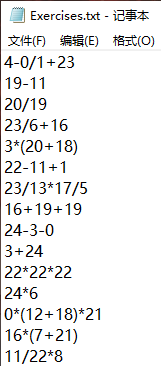
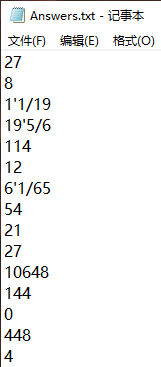
    　　3. 运行功能2：弹出UserAnswers.txt(给用户输入答案)：

    　　

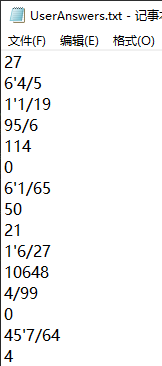
    　　4.运行功能3：:校验用户答案正确性，弹出Grade.txt(显示正确题序和错误题序)

    　　

    　　5..txt文件默认保存在E盘中

    　　

    　　6.运行说明：

    　　用随机数生成表达式时检查‘/’后面是否为零，若是则不生成，保证表达式除数不为0；还调用Answer()函数检查是否答案为负数，若是则不生成，保证表达式非负性；同时用一随机数chNum随机生成运算符个数，以保证运算符个数不超过三个；在Answer()函数中，求得结果后将分子大于分母的分式化为真分式，保证结果为真分式。在写项目过程中，每写完一模块就反复调试调用，以提高程序正确性。

    七、PSP表格：在程序各个模块的开发上实际耗费的时间

    PSP2.1

    Personal Software Process Stages

    预估耗时（分钟）

    实际耗时（分钟）

    Planning

    计划

     60

     75

    · Estimate

    · 估计这个任务需要多少时间

     60

     75

    Development

    开发

     2960

     3545

    · Analysis

    · 需求分析 (包括学习新技术)

     800

     1000

    · Design Spec

    · 生成设计文档

     120

     115

    · Design Review

    · 设计复审 (和同事审核设计文档)

     60

     50

    · Coding Standard

    · 代码规范 (为目前的开发制定合适的规范)

     60

     45

    · Design

    · 具体设计

     240

     255

    · Coding

    · 具体编码

     1000

     1200

    · Code Review

    · 代码复审

     200

     400

    · Test

    · 测试（自我测试，修改代码，提交修改）

     480

     480

    Reporting

    报告

     360

     395

    · Test Report

    · 测试报告

     180

     200

    · Size Measurement

    · 计算工作量

     120

     95

    · Postmortem & Process Improvement Plan

    · 事后总结, 并提出过程改进计划

     60

     100

    合计

     3380

     4015

    八、项目小结

    　　本次项目的细节较多，需要更加专注细心。比如一开始本想将表达式定义为String类型，但后来做的过程中发现总是要对字符串进行增加删除操作，为了提高运行效率，节省内存空间，查阅相关资料后准备转用为StringBuffer类型；还有在计算表达式的答案时，增添括号、负数统一表示形式、真分数处理和整型转换等都需要特别注意。

    　　此次项目采用结对编程形式，有了许多好处，比如在项目后期，我们查阅相关资料并讨论后发现可以用二叉树来生成含括号四则运算表达式，这样做会比我们用随机数生成括号会更加高效。平日一个人想不出的难题，可以通过两个人讨论解决；一个人陷入思维定式的误区时，另一个人可以指正。结对编程使我们思维更加开阔，编程效率更高。

    　　纪昂学：冷沐阳同学的学习能力挺强的，对于没涉及过的新知识，我们总是一起讨论学习，而且他的思维很活跃，经常想到一些我没想过的idea，这点在改bug的时候体现得尤为明显，经常注意到一些我忽略的细节。此次项目使我感受到结对编程的好处。

    　　冷沐阳：纪昂学同学能力强，工作态度上积极向上，头脑清晰，学习能力出众，总能迅速解决遇到的困难；有责任感，主动揽活，不偷懒，很大部分工作都是他完成的；善于交流 ，虽然有疫情的原因，不能够面对面交流，但纪昂学总能清楚的表达他的想法和思路。
  • 相关阅读:
    趣图：程序员告诉你为什么充钱后速度更快
    金三银四铜五铁六，面试得做好这个准备
    Java中如何模拟真正的同时并发请求？
    趣图：程序员最头疼的原因
    Java并发面试题
    linux内存分配与回收
    7.3 Set集合
    7.2 Java 11新增的Collection和Iterator接口
    7.1 Java集合概念
    6.5 正则表达式
  • 原文地址：https://www.cnblogs.com/3Jax/p/12610007.html
Copyright © 2011-2022 走看看