roc-charts 开发笔记：JS广度优先查找无向无权图两点间最短路径

广度优先查找无向无权图两点间最短路径，可以将图看成是以起点为根节点的树状图，每一层是上一层的子节点，一层一层的查找，直到找到目标节点为止。

起点为0度，与之相邻的节点为1度，以此类推。

    // 广度优先遍历查找两点间最短路径
    breadthFindShortestPath(sourceId, targetId) {
        const { nodesKV } = this.chart.getStore();
        let visitedNodes = [];  // 出现过的节点列表
        let degreeNodes = [[sourceId]];  // 二维数组，每个数组是每一度的节点列表。1度就是起点
        let degree = 0;  // 当前查找的度数
        let index = 0;  // 当前查找的当前度数节点数组中的索引
        let nodesParent = {};  // 记录每个节点的父节点是谁。广度优先遍历，每个节点就只有一个父节点
        let pathArr = [];  // 最短路径

        visitedNodes.push(sourceId);

        outer:
        while (degreeNodes[degree][index]) {

            degreeNodes[degree + 1] = degreeNodes[degree + 1] || [];  // 初始化下一度

            const node = nodesKV[degreeNodes[degree][index]];
            const neighborNodes = [...node.children || [], ...node.parents || []];

            for (let i = 0; i < neighborNodes.length; i++) {
                const id = neighborNodes[i];
                // 如果找到了，则退出
                if (id === targetId) {
                    nodesParent[id] = degreeNodes[degree][index];  // 记录目标节点的父节点是谁
                    break outer;
                } else if (!visitedNodes.includes(id)) {  // 如果没有找到，并且这个节点没有访问过，则把它添加到下一度中
                    visitedNodes.push(id);
                    degreeNodes[degree + 1].push(id);
                    nodesParent[id] = degreeNodes[degree][index];
                }
            }

            // 如果当前节点后面还有节点，则查找后一个节点
            if (degreeNodes[degree][index + 1]) {
                index++;
            } else {
                degree++;
                index = 0;
            }
        }

        // 通过目标节点的父节点，层层追溯找到起点，得到最短路径
        let nodeId;
        nodeId = targetId;
        while (nodeId) {
            pathArr.push(nodeId);
            // 当前节点有父节点，则将 nodeId 设置为父节点的 id，继续循环查找父节点
            if (nodesParent[nodeId]) {
                pathArr.push(nodesParent[nodeId]);
                nodeId = nodesParent[nodeId];  // nodeId 设置为父节点的 id
            } else {  // 没有父节点，则说明到了起点。nodeId 设为 null，退出循环
                nodeId = null;
            }
        }

        return pathArr;
    }

上面代码中，主要的数据结构有：

visitedNodes：一层层的查找，出现的节点立刻添加到这个数组中。当查找一个节点的相邻节点时，如果相邻节点是它的父节点或同一度的节点，那这个节点就已经在 visitedNodes 中了，不会将此节点标记为这个节点的子节点。

degreeNodes：数组中的每个数组，就是0度至N度，每一度的节点列表。

nodesParent：查找节点时，会将当前节点标记为相邻节点的父节点（除了已经在 visitedNodes 中的，visitedNodes 中的节点都已有了父节点），每个节点只有一个父节点。

假设下图中1号节点为开始节点，15号节点为目标节点：

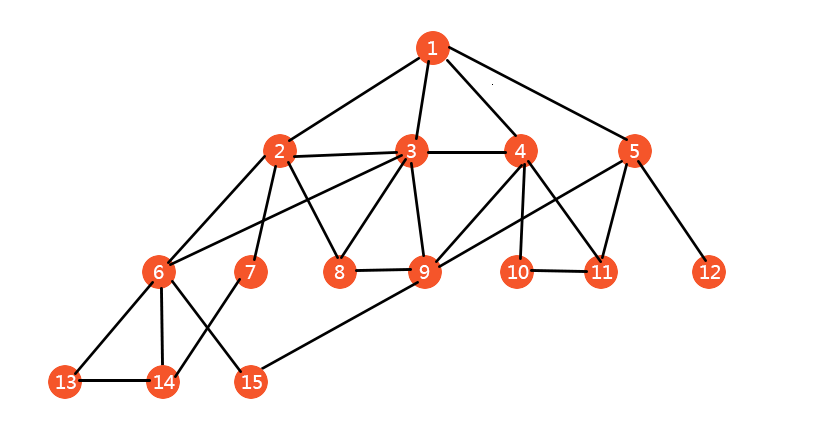
情况分析：

1、1号节点开始查找，找到相邻节点2,3,4,5号，2,3,4,5号节点都没在 visitedNodes 中，将它们添加到 visitedNodes 里，并且将它们添加到 degreeNodes 中下一度的数组中。此时 visitedNodes 里面就有1,2,3,4,5号节点，nodesParent 里面，2,3,4,5号节点的父节点都是1号节点。

2、1号节点后面没有与之同度数的节点，degree 加1，index 重置为0。

3、2号节点开始查找，相邻节点中有1,3,6,7,8号节点，图中可以看出1号节点和3号节点是它的父节点和同度数的节点，这两个节点已经被添加到了 visitedNodes 中，则只将6,7,8号节点添加到 degreeNodes 中下一度的数组中。nodesParent 里面，6,7,8号节点的父节点都设置为2号节点。visitedNodes 中添加6,7,8号节点。

4、2号节点的相邻节点遍历完成后，判断2号节点后面是否有相同度数的节点，degreeNodes[degree][index + 1] 发现不为空，则 index++ 继续循环查到当前度数的下一个节点的相邻节点。

5、开始查找3号节点的相邻节点，1,2,4,6,8,9号节点都是3号节点的相邻节点，而1,2,4,6,8号节点都已在 visitedNodes 中，则只将9号节点的父节点设置为3号节点。

6、同理，继续判断3号节点后是否有相同度数的节点，有4号节点，继续查找，有5号节点，继续查找。

7、当找到12号节点后，继续查找5号节点后是否有相同度数的节点，degreeNodes[degree][index + 1]  的值为 undefined 了，则 degree++, index = 0 继续循环找下一度的节点。

8、通过6号节点的相邻节点，找到了15号节点，此时退出循环，通过 nodesParent 得到最短路径 15-6-2-1。

当然，我们也能从图中看出1-3-6-15，1-3-9-15和1-5-9-15也是最短路径，不过这不重要，找到一条即可。这也是为什么 nodesParent 里面6号节点的父节点只设置2号而不用设置3号，一个节点只设置一个父节点，因为无论从哪个父节点查找，路径长度是一样的。