判断题:







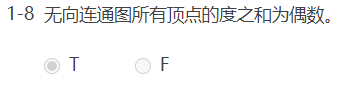
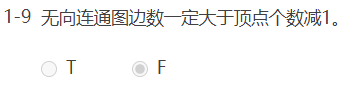

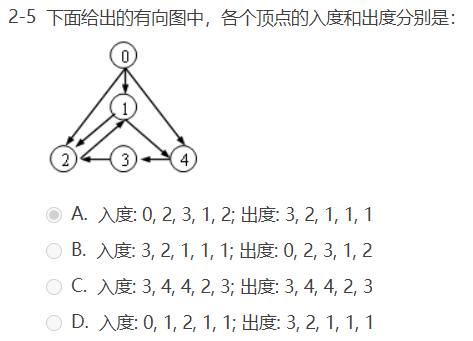
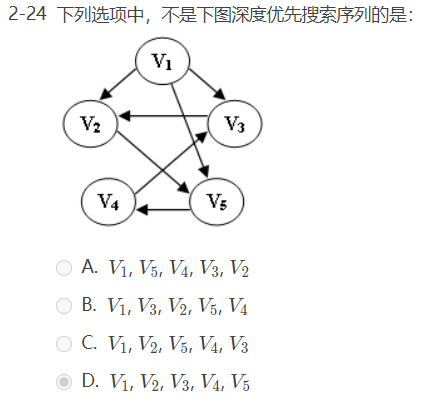
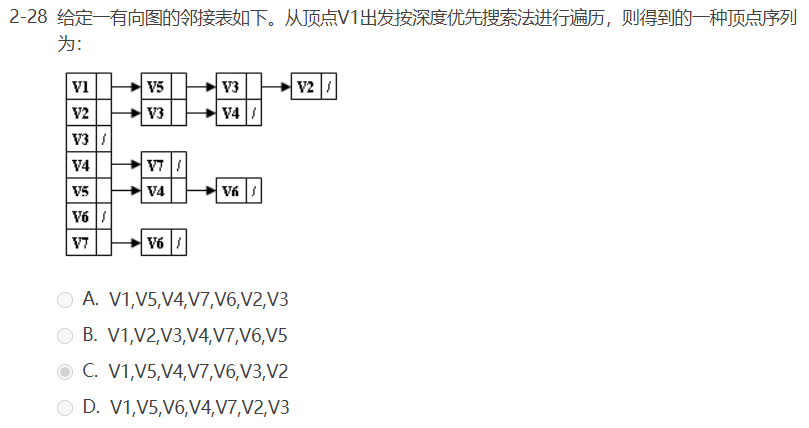
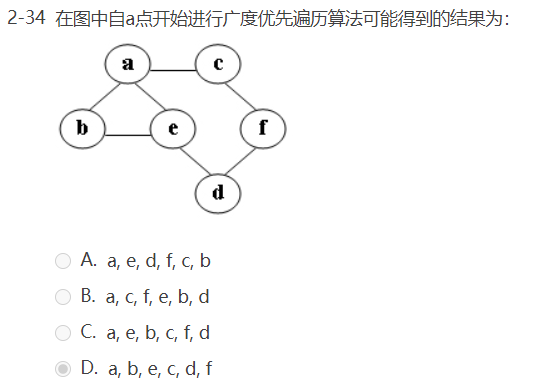
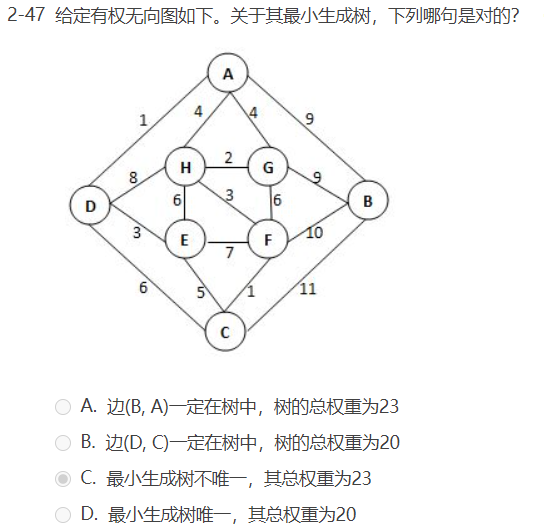
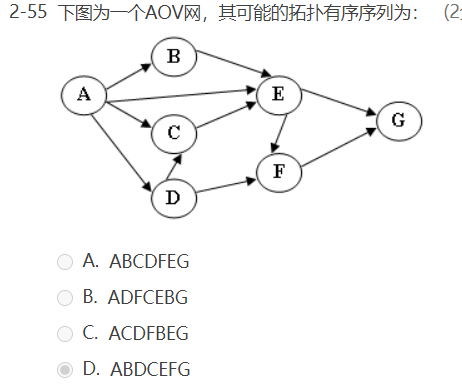
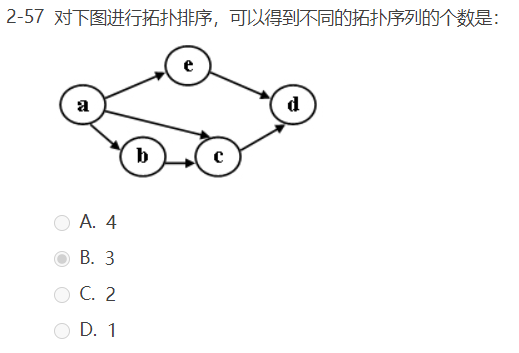
选择题:

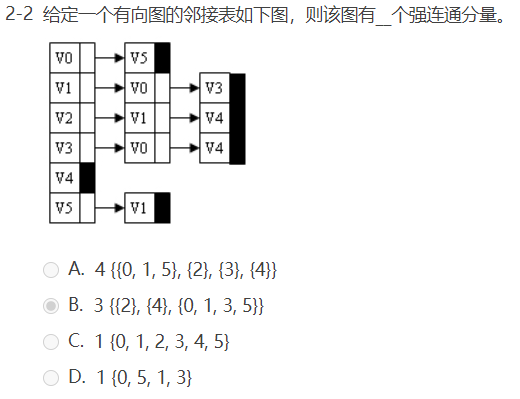

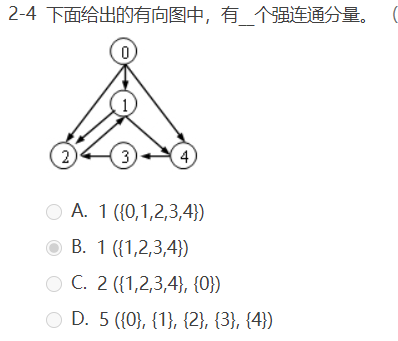


























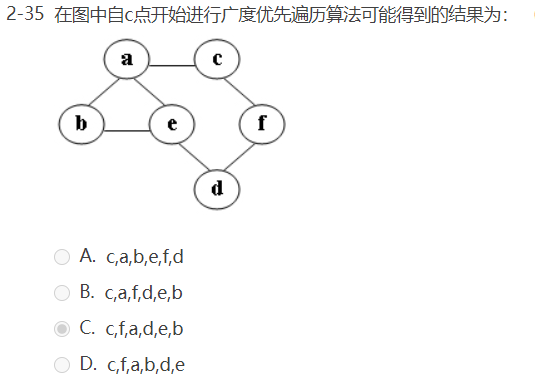

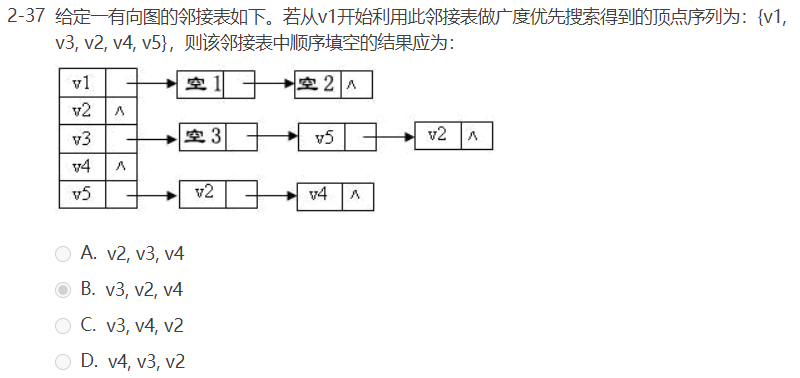




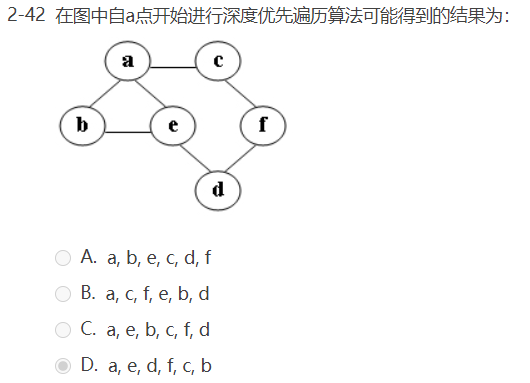



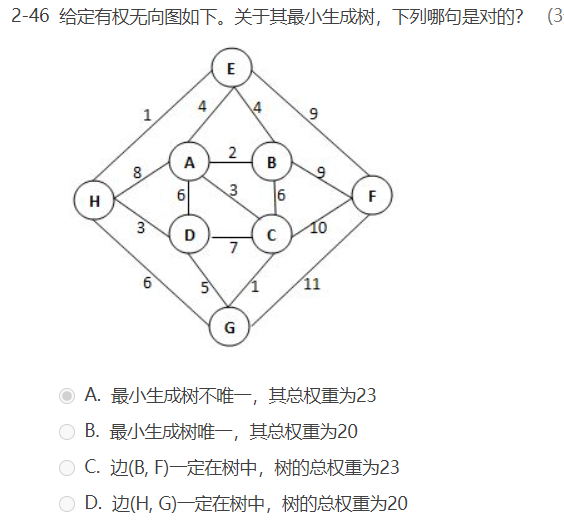









函数题:
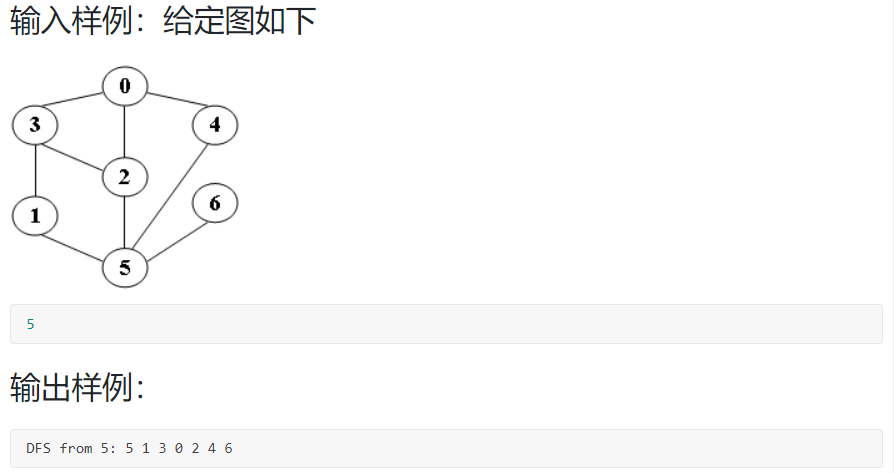
6-1 邻接矩阵存储图的深度优先遍历:
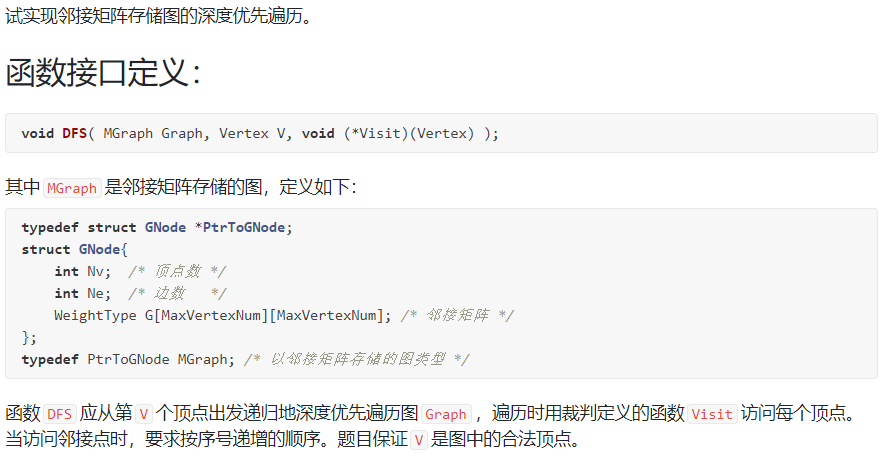
裁判测试程序样例:
#include <stdio.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 /* 最大顶点数设为10 */
#define INFINITY 65535 /* ∞设为双字节无符号整数的最大值65535*/
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
typedef int WeightType; /* 边的权值设为整型 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
WeightType G[MaxVertexNum][MaxVertexNum]; /* 邻接矩阵 */
};
typedef PtrToGNode MGraph; /* 以邻接矩阵存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */
MGraph CreateGraph(); /* 创建图并且将Visited初始化为false;裁判实现,细节不表 */
void Visit( Vertex V )
{
printf(" %d", V);
}
void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) );
int main()
{
MGraph G;
Vertex V;
G = CreateGraph();
scanf("%d", &V);
printf("DFS from %d:", V);
DFS(G, V, Visit);
return 0;
}
/* 你的代码将被嵌在这里 */
代码:

void DFS( MGraph Graph, Vertex V, void (*Visit)(Vertex) )
{
Visit(V);
Visited[V] = true;
for(int i=0;i<Graph->Nv;i++)
{
if((Graph->G[V][i]==1)&&(!Visited[i]))//1代表相通,Visited非1代表没有访问过
DFS(Graph, i, Visit);//递归
}
}
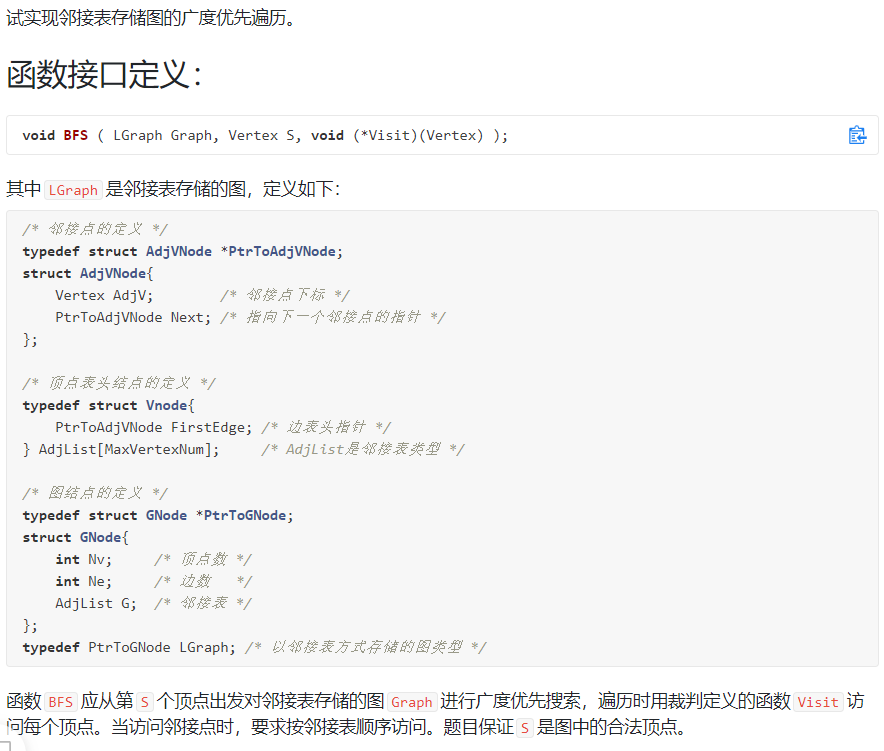
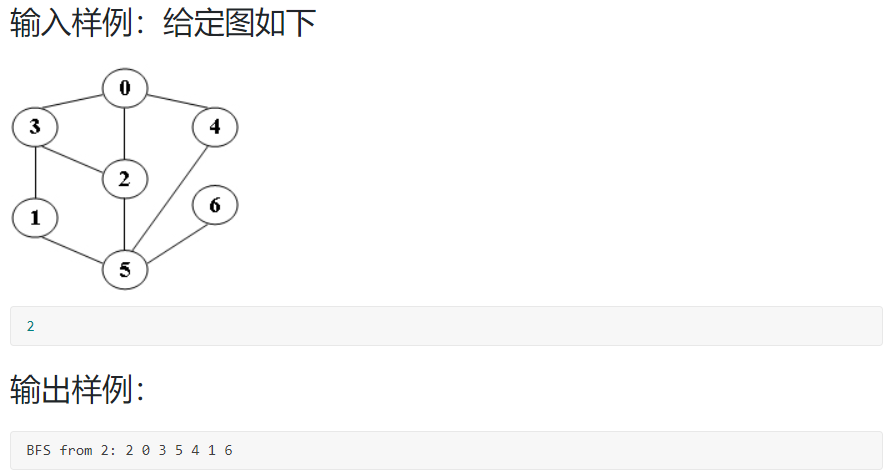
6-2 邻接表存储图的广度优先遍历:
裁判测试程序样例:
#include <stdio.h>
typedef enum {false, true} bool;
#define MaxVertexNum 10 /* 最大顶点数设为10 */
typedef int Vertex; /* 用顶点下标表示顶点,为整型 */
/* 邻接点的定义 */
typedef struct AdjVNode *PtrToAdjVNode;
struct AdjVNode{
Vertex AdjV; /* 邻接点下标 */
PtrToAdjVNode Next; /* 指向下一个邻接点的指针 */
};
/* 顶点表头结点的定义 */
typedef struct Vnode{
PtrToAdjVNode FirstEdge; /* 边表头指针 */
} AdjList[MaxVertexNum]; /* AdjList是邻接表类型 */
/* 图结点的定义 */
typedef struct GNode *PtrToGNode;
struct GNode{
int Nv; /* 顶点数 */
int Ne; /* 边数 */
AdjList G; /* 邻接表 */
};
typedef PtrToGNode LGraph; /* 以邻接表方式存储的图类型 */
bool Visited[MaxVertexNum]; /* 顶点的访问标记 */
LGraph CreateGraph(); /* 创建图并且将Visited初始化为false;裁判实现,细节不表 */
void Visit( Vertex V )
{
printf(" %d", V);
}
void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) );
int main()
{
LGraph G;
Vertex S;
G = CreateGraph();
scanf("%d", &S);
printf("BFS from %d:", S);
BFS(G, S, Visit);
return 0;
}
/* 你的代码将被嵌在这里 */
代码:

void BFS ( LGraph Graph, Vertex S, void (*Visit)(Vertex) )
{
Vertex v[11];//利用一个数组队列存储遍历的节点
PtrToAdjVNode ptg;
int i=0;
int j=0;
v[j++]=S;
Visited[S] = true;//标记为已遍历
while(i<j)
{
Vertex vv = v[i++];
Visit(vv);//输出首位
ptg = Graph->G[vv].FirstEdge;//指向输出的队首的指针
while(ptg)//将输出的队首的未遍历的子节点入队
{
if(!Visited[ptg->AdjV])
{
v[j++] = ptg->AdjV;
Visited[ptg->AdjV] = true;
}
ptg = ptg->Next;
}
}
}
7-1 畅通工程之局部最小花费问题:

输入样例:
4
1 2 1 1
1 3 4 0
1 4 1 1
2 3 3 0
2 4 2 1
3 4 5 0
输出样例:
3
代码:

#include<stdio.h>
int main()
{
int dist[105],cost[105][105],visit[105]={0};
int i,j;
int n,m,sum=0;
scanf("%d", &n);
for(i=1;i<=n;i++){//每个点赋初值
for(j=1;j<=n;j++){
cost[i][j]=cost[j][i]=99999;
}
}
m = n*(n-1)/2;
int a,b,chengben,zhuangtai;
while(m--)
{
scanf("%d%d%d%d", &a, &b, &chengben, &zhuangtai);
if(zhuangtai == 0)
cost[a][b] = cost[b][a] = chengben;
else
cost[a][b] = cost[b][a] = 0;
}
for(j=1;j<=n;j++)//编号从1开始
dist[j] = cost[1][j];
visit[1] = 1;
dist[1] = 0;
for(i=1;i<n;i++)
{
int min=99999;
int flag=-1;
for(j=1;j<=n;j++)//以1号城镇为起点,找到距离1号城镇最近的城
{
if(visit[j]==0 && dist[j]<min)
{
min = dist[j];
flag=j;
}
}
visit[flag]=1;
if(flag!=-1)
{
sum+=dist[flag];//jiang成本算入
for(j=1;j<=n;j++)//已经找到距离1最近的k点,再以k为起点
{
if(visit[j]==0 && dist[j]>cost[flag][j])
dist[j] = cost[flag][j];
}
}
}
printf("%d
",sum);
return 0;
}
7-2 畅通工程之最低成本建设问题:

输入样例1:
6 15
1 2 5
1 3 3
1 4 7
1 5 4
1 6 2
2 3 4
2 4 6
2 5 2
2 6 6
3 4 6
3 5 1
3 6 1
4 5 10
4 6 8
5 6 3
输出样例1:
12
输入样例2:
5 4
1 2 1
2 3 2
3 1 3
4 5 4
输出样例2:
Impossible
代码:

#include<stdio.h>
int main()
{
int n,m,sum=0;
int arr[1005][1005];
scanf("%d%d",&n,&m);
int dist[1001]={999999};// dist[i] 表示i节点到已有生成树的最短距离
for(int i=1;i<=n;i++)//初始化矩阵,每个点为 ∞
for(int j=1;j<=m;j++)
arr[i][j]=999999;
int x,y,z;
int flag=1;
for(int i=0;i<m;i++)//生成邻接矩阵
{
scanf("%d%d%d",&x,&y,&z);
arr[x][y] = arr[y][x] = z;
}
for(int i=1;i<=n;i++)//记录每个点到1的最短距离
dist[i] = arr[1][i];
dist[1] = 0;// 访问过的点设为0
while(1)
{
int a=0;
for(int i=1;i<=n;i++)
{
if(dist[i]<dist[a] && dist[i])
a = i;
}
if(!a)
break;
sum += dist[a];
dist[a] = 0;
for(int i=1;i<=n;i++)
{
if(arr[a][i] < dist[i])
dist[i] = arr[a][i];
}
}
for(int i=1;i<=n;i++)
{
if(dist[i])
flag=0;
}
if(!flag)
printf("Impossible
");
else
printf("%d
",sum);
return 0;
}
7-3 城市间紧急救援:

输入样例:
4 5 0 3
20 30 40 10
0 1 1
1 3 2
0 3 3
0 2 2
2 3 2
输出样例:
2 60
0 1 3
代码:

#include <stdio.h>
#include <string.h>
#define INF 999999
int n, m, s, d, vis[505], l[505][505], dis[505], p[505], sum[505], ans[505];
void dfs(int length, int people, int dd)
{
int i;
if(dd == s)
return;
for(i = 0 ; i < n ; i++)
{
if(length - l[dd][i] == dis[i] && people - p[dd] == sum[i])
{
dfs(dis[i], sum[i], i);
printf("%d ", i);
break;
}
}
}
void dij()
{
int i, j, k, min;
vis[s] = 1;
sum[s] = p[s];
ans[s] = 1;
for(i = 0 ; i < n ; i++)
{
dis[i] = l[s][i];
if(s != i && l[s][i] != INF)
{
sum[i] = p[i] + p[s];
ans[i] = 1;//
}
}
for(i = 0 ; i < n-1 ; i++)
{
min = INF;
for(j = 0 ; j < n ; j++)
{
if(!vis[j] && min > dis[j])
{
min = dis[j];
k = j;
}
}
vis[k] = 1;
for(j = 0 ; j < n; j++)
{
if(!vis[j])
{
if(dis[j] > dis[k] + l[k][j])
{
dis[j] = dis[k] + l[k][j];
sum[j] = sum[k] + p[j];
ans[j] = ans[k];//
}
else if(dis[j] == dis[k] + l[k][j])
{
ans[j] += ans[k];//
if(sum[j] < sum[k] + p[j])
{
sum[j] = sum[k] + p[j];
}
}
}
}
}
}
int main()
{
int i, j, x, y, ll;
scanf("%d %d %d %d", &n, &m, &s, &d);
for(i = 0 ; i < n ; i++)
for(j = 0 ; j < n ; j++)
{
l[i][j] = INF;
}
for(i = 0 ; i < n; i++)
{
scanf("%d", &p[i]);
}
for(i = 0 ; i < m ; i++)
{
scanf("%d %d %d", &x, &y, &ll);
l[x][y] = l[y][x] = ll;
}
if(n == 1)
{
printf("1 %d
1", p[0]);
return 0;
}
dij();
printf("%d %d
", ans[d], sum[d]);
printf("%d ", s);
dfs(dis[d], sum[d], d);
printf("%d", d);
return 0;
}
7-4 天梯地图:
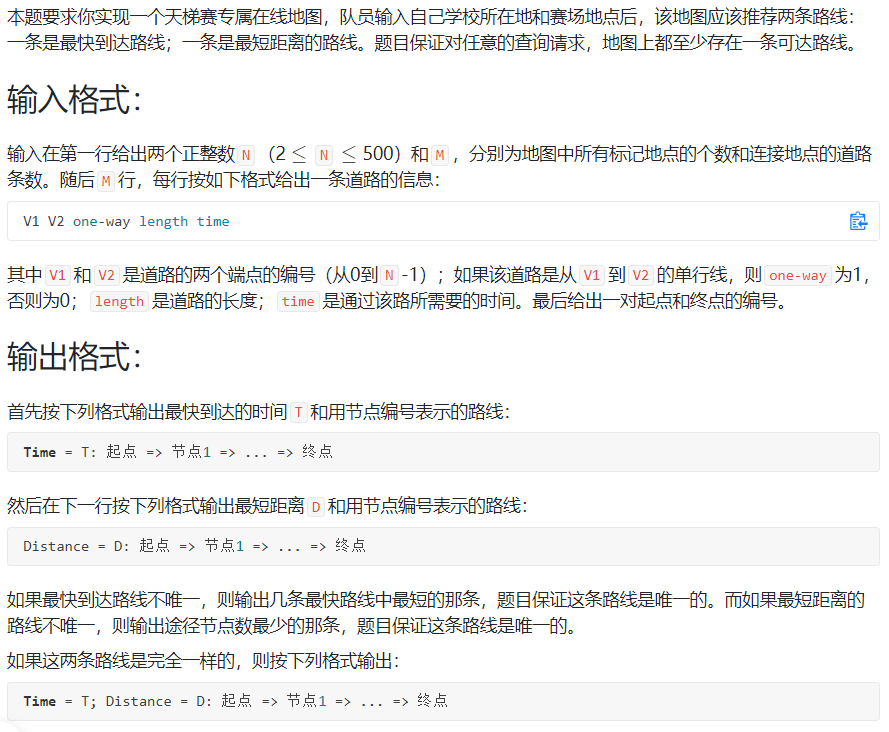
输入样例1:
10 15
0 1 0 1 1
8 0 0 1 1
4 8 1 1 1
5 4 0 2 3
5 9 1 1 4
0 6 0 1 1
7 3 1 1 2
8 3 1 1 2
2 5 0 2 2
2 1 1 1 1
1 5 0 1 3
1 4 0 1 1
9 7 1 1 3
3 1 0 2 5
6 3 1 2 1
5 3
输出样例1:
Time = 6: 5 => 4 => 8 => 3
Distance = 3: 5 => 1 => 3
输入样例2:
7 9
0 4 1 1 1
1 6 1 3 1
2 6 1 1 1
2 5 1 2 2
3 0 0 1 1
3 1 1 3 1
3 2 1 2 1
4 5 0 2 2
6 5 1 2 1
3 5
输出样例2:
Time = 3; Distance = 4: 3 => 2 => 5
代码:

#include<stdio.h>
#include<iostream>
using namespace std;
int sum[521];//记录找最短时间时到原点的距离
struct
{
int length;
int time;
}Graph[521][521];//建立地图
struct
{
int visit;
int length;
int pre;
}LVisit[521];//建立距离、访问表
struct
{
int visit;
int time;
int pre;
}TVisit[521];//建立时间、访问表
void InitGraph(int N, int M)//创建并初始化地图
{
for(int i=0; i<=N; i++)//初始化各点间的距离和时间均为无穷大
for(int j=0; j<=N; j++){
sum[j] = 0;
Graph[i][j].length = 9999999;
Graph[i][j].time = 9999999;
}
int v1, v2, way, length, time;
for(int i=0; i<M; i++){//读取输入创建地图
cin>>v1>>v2>>way>>length>>time;
Graph[v1][v2].length = length;
Graph[v1][v2].time = time;
if(way == 0){//非单行线,两地可互通
Graph[v2][v1].length = length;
Graph[v2][v1].time = time;
}
}
}
void InitVisit(int N, int S)// 初始化时间、距离、访问表
{
for(int i=0; i<=N; i++){
LVisit[i].visit = 0;//初始化为未访问
LVisit[i].length = Graph[S][i].length;//根据地图初始化到原点距离
TVisit[i].visit = 0;//初始化为未访问
TVisit[i].time = Graph[S][i].time;//根据地图初始化时间
if(TVisit[i].time!=9999999){//如果和原点相通设置前驱点为原点,并设置个时间点到原点距离
LVisit[i].pre = S;
TVisit[i].pre = S;
sum[i] = Graph[S][i].length;
}
}
LVisit[S].visit = 1;//设置原点已访问
TVisit[S].visit = 1;//设置原点已访问
}
void DST_L(int N, int S)//斯特拉求最短距离
{
for(int j=1; j<N; j++){
int mlpoint = N;//设置N点为最近点,N点已设为无穷远
for(int i=0; i<N; i++){
if(LVisit[i].length<LVisit[mlpoint].length&&!LVisit[i].visit)
mlpoint = i;
}//求出最近点并设置为已访问
LVisit[mlpoint].visit = 1;
for(int i=0; i<N; i++){//更新距离
if(!LVisit[i].visit){
//更新为更短的距离
if(LVisit[i].length>LVisit[mlpoint].length+Graph[mlpoint][i].length){
LVisit[i].length = LVisit[mlpoint].length+Graph[mlpoint][i].length;
LVisit[i].pre = mlpoint;//设置前驱点
}
//距离相同则节点少为优
else if(LVisit[i].length==LVisit[mlpoint].length+Graph[mlpoint][i].length){
int l1=0,l2=0;
int pre = LVisit[i].pre;
while(pre!=S){
l1++;
pre = LVisit[pre].pre;
}
pre = mlpoint;
while(pre!=S){
l2++;
pre = LVisit[pre].pre;
}
if(l1>l2)//节点多则更新
LVisit[i].pre = mlpoint;
}
}
}
}
}
void DST_T(int N, int S)//斯特拉求最短时间
{
for(int j=1; j<N; j++){
int mtpoint = N;//无穷为最短点
for(int i=0; i<N; i++){
if(TVisit[i].time<TVisit[mtpoint].time&&!TVisit[i].visit)
mtpoint = i;
}//求出最短点并设置为已访问
TVisit[mtpoint].visit = 1;
for(int i=0; i<N; i++){
if(!TVisit[i].visit){
//更新最短时间
if(TVisit[i].time>TVisit[mtpoint].time+Graph[mtpoint][i].time){
TVisit[i].time = TVisit[mtpoint].time+Graph[mtpoint][i].time;
TVisit[i].pre = mtpoint;
sum[i] = sum[mtpoint] + Graph[mtpoint][i].length;//更新最短时间的距离
}//时间相同则根据距离更新,距离短的优先
else if(TVisit[i].time==TVisit[mtpoint].time+Graph[mtpoint][i].time){
if(sum[i]>sum[mtpoint]+Graph[mtpoint][i].length){//选距离更短的
TVisit[i].pre = mtpoint;
sum[i] = sum[mtpoint] + Graph[mtpoint][i].length;//更新其距离
}
}
}
}
}
}
int main()
{
int N, M;
cin>>N>>M;
InitGraph(N,M);//初始化并读取输入创建图
int S, D;
cin>>S>>D;
InitVisit(N, S);//创建并初始化距离、时间、访问表
DST_L(N,S);//求最短距离
DST_T(N,S);//求最短时间
int lpath[521];//最短距离路径表
int tpath[521];//最短时间路径表
int l=520, t=520;;
int pre = D;
while(pre!=S){//根据目的地不断往后后移,直到后移到原点
lpath[l]=pre;
pre = LVisit[pre].pre;
l--;
}
pre = D;
while(pre!=S){
tpath[t] = pre;
pre = TVisit[pre].pre;
t--;
}
if(t==l){//路径长度一样
int flag = 0;
for(int i=t+1; i<521; i++){//判断路径是否完全相同
if(tpath[i]!=lpath[i])
flag = 1;//不相等
}
if(flag == 1){//路径不同
cout<<"Time = "<<TVisit[D].time<<": "<<S;
for(int i = t+1; i<521; i++){
cout<<" => "<<tpath[i];
}
cout<<endl;
cout<<"Distance = "<<LVisit[D].length<<": "<<S;
for(int i = l+1; i<521; i++){
cout<<" => "<<lpath[i];
}
}
else{//路径相同
cout<<"Time = "<<TVisit[D].time<<"; "<<"Distance = "<<LVisit[D].length<<": "<<S;
for(int i = t+1; i<521; i++){
cout<<" => "<<tpath[i];
}
}
return 0;
}
//路径不同
cout<<"Time = "<<TVisit[D].time<<": "<<S;
for(int i = t+1; i<521; i++){
cout<<" => "<<tpath[i];
}
cout<<endl;
cout<<"Distance = "<<LVisit[D].length<<": "<<S;
for(int i = l+1; i<521; i++){
cout<<" => "<<lpath[i];
}
}
7-5 关键活动:

输入样例:
7 8
1 2 4
1 3 3
2 4 5
3 4 3
4 5 1
4 6 6
5 7 5
6 7 2
输出样例:
17
1->2
2->4
4->6
6->7
代码:

#include<stdio.h>
#include<stdlib.h>
#define MaxSize 10000
typedef struct Node {
int El;
int La;
}Nodes;
int main() {
int n, m;
scanf("%d %d", &n, &m);
int DEEP[101] = { 0 }; //保存点的度数
int sort[101] = { 0 }; //保存排序结果
int a[101][101] = { 0 }; //保存路径长度
int end[101];
int b[101][101]; //保存关键路径
int sunxu[101]; //保存顺序
Nodes *N = (Nodes *)malloc(sizeof(Nodes)*(n+1));
for (int i = 1; i <= n; i++)
{
end[i] = -1;
N[i].El = 0;
N[i].La = MaxSize;
for (int j = 1; j <= n; j++)
{
a[i][j] = -1;
b[i][j] = -1;
}
}
int qi, zhong, chang, count = 0, px = 0, countt = 1;
for (int j = 1; j <= m; j++)
{
px = 0;
scanf("%d %d %d", &qi, &zhong, &chang);
a[qi][zhong] = chang;
DEEP[zhong]++;
for (int y = 1; y < j; y++)
{
if (zhong == sunxu[y]) {
px = 1;
break;
}
}
if (px != 1) {
sunxu[countt] = zhong;
countt ++ ;
}
}
int ss = 1, flag = 0,isend=1,QQ=1;
for (int i = 1; i <= n; i++)
{
int z=1,isend=1;
for (z = 1; z<=n; z++)
{
if (a[i][z] != -1) { isend = 0; break; } //不是结束点
}
if (isend == 1) {
end[count] = i;
count++;
}
flag = -1;
for (int j = 1; j <= n; j++)
{
if (DEEP[j] == 0) {
flag = 0;
DEEP[j] = -1;
sort[ss] = j;
ss++;
for (int k = 1; k <= n; k++)
{
if (a[j][k] != -1) {
DEEP[k]--;
}
}
break;
}
}
if (flag == -1) {
break;
}
}
if (flag == 0) {
int max = 0;
for (int i = 1; i <= n; i++)
{
for (int j = 1; j <= n; j++)
{
if (a[j][sort[i]] != -1) {
if (N[sort[i]].El < N[j].El + a[j][sort[i]]) {
N[sort[i]].El = a[j][sort[i]] + N[j].El;
}
}
}
}
for (int i = 1; i <= n; i++)
{
if (N[i].El > max) {
max = N[i].El;
}
}
printf("%d
", max); int lengths = 0;
for (int z = 0; z < count; z++)
{
N[end[z]].La = max;
}
for (int l = n; l>=1; l--)
{
for (int i = 1; i <=n; i++)
{
if (a[i][sort[l]]!=-1) {
if (N[sort[l]].La - a[i][sort[l]] < N[i].La) {
N[i].La = N[sort[l]].La - a[i][sort[l]];
}
}
}
for (int x = 1; x <=n; x++)
{
if (a[x][sort[l]] != -1) {
if (N[sort[l]].La - a[x][sort[l]] == N[x].La&&N[x].La== N[x].El) {
b[x][sort[l]] = 1;
lengths++;
}
}
}
}
for (int p = 1; p <= n; p++) {
for (int k = countt - 1; k >= 1; k--) {
if (b[p][sunxu[k]] == 1) {
printf("%d->%d", p, sunxu[k]);
lengths--;
printf("
");
}
}
}
}
else {
printf("0");
}
return 0;
}
