我们先了解有序数组和链表两种数据结构:有序数组,可以通过二分查找法快速的查询特定的值,时间复杂度为O(logN),可是插入删除时效率低,平均要移动N/2个元素,时间复杂度为O(N)。链表:查询效率低,平均要比较N/2个元素,时间复杂度O(N),插入和删除效率较高,O(1)。二叉树的特点是结合了有序数组和链表的优点,能像有序数组那样快速的查找,又能像链表那样快速的插入和删除。操作二叉搜索树的时间复杂度是O(logN)。
1.定义
二叉树:树中的每个节点最多只能有两个子节点,这样的树是二叉树。
二叉搜索树:一个节点的左子节点的关键字值小于这个父节点,右子节点的关键字值大于等于这个父节点。
平衡二叉搜索树:它是一颗裸空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两棵子树都是平衡二叉树。它的实现方式有:红黑树,AVL
2.结构图
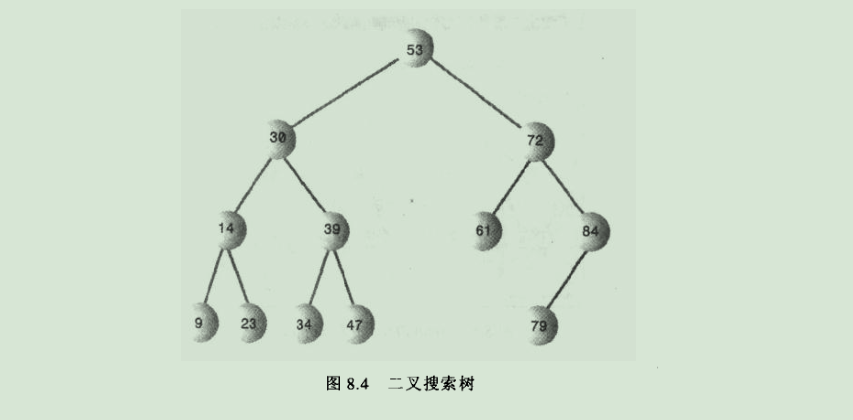
二叉树由节点和边构成,每个节点包含的有关键字值,以及其他数据。接下来我们通过代码看如何对二叉搜索树进行插入,删除,查找,遍历等操作。
3.查找操作
先定义节点Node
public class Node { int key; //key 关键字值 double data; //存储的数据 Node leftChild; //左子节点的引用 Node rightChild; //右子节点的引用 //显示该节点内容 public void displayNode(){ System.out.println("key="+key+",data="+data); } }
定义二叉树Tree
public class Tree { //根节点 public Node root;
}
查找方法:将关键字值key与根节点的关键字值做比较,小于root节点的关键字值,进入root节点的左子树进行比较;否则如果大于,进入root节点的右子树进行比较。依次比较下去,直到key的值等于某个节点的关键字值,则将该节点Node返回。如果没有找到
符合条件的节点,那么返回null
//查询效率和有序数组中的二分查找法一样,时间复杂度为O(log2N) public Node find(int key){ Node current = root; while (current.key != key) { if(key < current.key) current = current.leftChild; else{ current = current.rightChild; } //表示没有找到符合条件的节点 if (null == current) return null; } return current; }
4.插入操作
插入操作,先要确定新节点要插入的位置,这个就是查找的过程;然后确定位置后,将新节点newNode作为父节点parent的的左子节点或者右子节点
//插入方法:查找最后一个不为null的节点parent作为要插入节点的父节点,newNode作为它的左子节点或者右子节点 public void insert(int key,double data){ Node newNode = new Node(); newNode.key = key; newNode.data = data; if(null == root){ root = newNode; }else{ Node current = root; Node parent; while(true){ parent = current; if(key < current.key){ //go left current = current.leftChild; if(null == current){ parent.leftChild = newNode; return; } }else{ //go right current = current.rightChild; if(null == current){ parent.rightChild = newNode; return; } } } } }
5.遍历操作
遍历操作,是指根据特定的顺序访问树的每一个节点。遍历方法有:中序遍历,前序遍历,后序遍历
中序遍历,会使所有节点按照关键字值的升序被访问到。遍历时,通常使用递归调用的方法,初始参数是树的根节点。中序遍历会有三个步骤:
* 调用自身来遍历该节点的左子树
* 访问这个节点
* 调用自身来遍历该节点的右子树
//中序遍历二叉树:按key值的升序排序 public void orderByMiddle(Node localRoot){ if(null != localRoot){ orderByMiddle(localRoot.leftChild); System.out.println(localRoot.data); orderByMiddle(localRoot.rightChild); } } //前序遍历二叉树 public void preOrder(Node localRoot){ if(null != localRoot){ System.out.println(localRoot.data); preOrder(localRoot.leftChild); preOrder(localRoot.rightChild); } } //后序遍历二叉树 public void postOrder(Node localRoot){ if(null != localRoot){ postOrder(localRoot.leftChild); postOrder(localRoot.rightChild); System.out.println(localRoot.data); } }
6.查找最大值和最小值
查找最大值,从根节点开始走向右子节点,然后一直走向右子节点,直到最后一个不为null的右子节点,就是最大值。查找最小值,是类似的,一直走向左子节点。
//查找最大值 public Node maxNum() { Node current,last = null; current = root; while (null != current) { last = current; current = current.rightChild; } return last; } //查找最小值 public Node miniNum() { Node current,last = null; current = root; while (null != current) { last = current; current = current.leftChild; } return last; }
7.删除操作
对于删除操作的逻辑如下:
* 要先判断被删除的节点的情况,然后分别处理,被删除节点可能是:是叶节点,只有一个子节点,有两个子节点
* 如果被删除节点有两个子节点:找到要删除节点的后继节点,然后让后继节点替换该节点。由于二叉搜索树要满足的特性是一个节点的左子节点的key值要比该节点小,右子节点的key值要比该节点大,所以,一个节点的后继节点就是比该节点key值大的最小的那个节点。也就是该节点的右子节点的左子节点,再左子节点,直到最后一个不是null的左子节点,就是该节点的后继节点。找到后继节点后,就将后继节点替换当前节点,涉及到各个节点引用的改变,有四个地方的引用改变,也就是代码中的abcd四个步骤。
如果要删除的节点有两个子节点,看图:
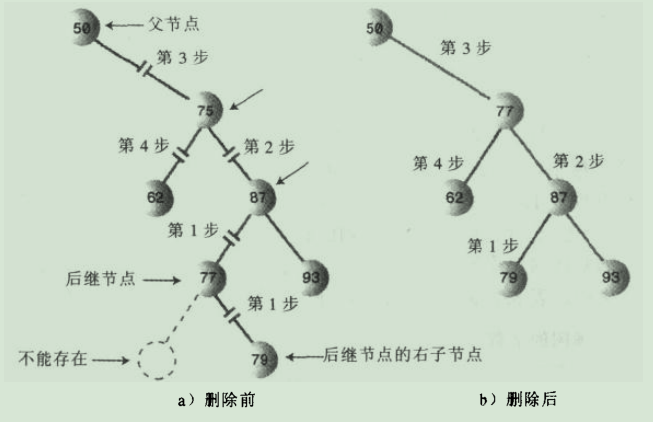
//删除方法 //1.要删除的节点是叶节点 2.只有一个字节点 3.有两个子节点 //步骤:1.先找到要删除的节点 public boolean delete(int key){ //1.先查找到要删除的节点 Node current = root; Node parent = root; //标识被删除的节点是否是左子节点 boolean isLeftChild = true; while(key != current.key){ parent = current; if(key < current.key){ current = current.leftChild; isLeftChild = true; }else{ current = current.rightChild; isLeftChild = false; } //没有找到要删除的节点 if(null == current){ return false; } } //2.如果该节点没有子节点 if(null == current.leftChild && null == current.rightChild){ //判断该节点是否是根节点 if(current == root){ root = null; }else if(isLeftChild) { parent.leftChild = null; }else{ parent.rightChild = null; } //3.如果该节点只有一个子节点:左子节点 }else if(null == current.rightChild){ //被删除的节点如果是根节点 if(current == root){ root = current.leftChild; }else if(isLeftChild){ parent.leftChild = current.leftChild; }else{ parent.rightChild = current.leftChild; } //4.如果该节点只有一个子节点:右子节点 }else if(null == current.leftChild){ if(current == root){ root = current.rightChild; }else if(isLeftChild){ parent.leftChild = current.rightChild; }else{ parent.rightChild = current.rightChild; } //5.如果要删除的节点有两个子节点:需要找到该节点的后继节点代替该节点,后继节点就是key值比当前节点大的那个最小的值 }else{ //先找到后继节点successor Node successor = getSuccessor(current); if(current == root){ root = successor; }else if(isLeftChild){ //c 将后继节点赋值给要删除节点的父节点的左子节点 parent.leftChild = successor; }else{ //c 将后继节点赋值给要删除节点的父节点的右子节点 parent.rightChild = successor; } //d 将要删除节点的左子节点赋值给后继节点的左子节点 successor.leftChild = current.leftChild; } return true; } //查找后继节点,并替换部分引用 a,b private Node getSuccessor(Node delNode){ Node successorParent = delNode; Node successor = delNode; Node current = delNode.rightChild; while (current != null) { successorParent = successor; successor = current; current = current.leftChild; } if(successor != delNode.rightChild){ successorParent.leftChild = successor.rightChild; //a 把后继节点的右子节点赋值给后继节点的父节点的左子节点 successor.rightChild = delNode.rightChild; //b 把要删除节点的右子节点赋值给后继节点的右子节点 } return successor; }
8.用数组表示二叉树
其实,除了以上那种方式表示二叉树外,还可以用数组表示二叉树。用数组时,节点存储在数组中,节点再数组中的位置对应于它在树中的位置,通过下图可以理解它的存储方式。
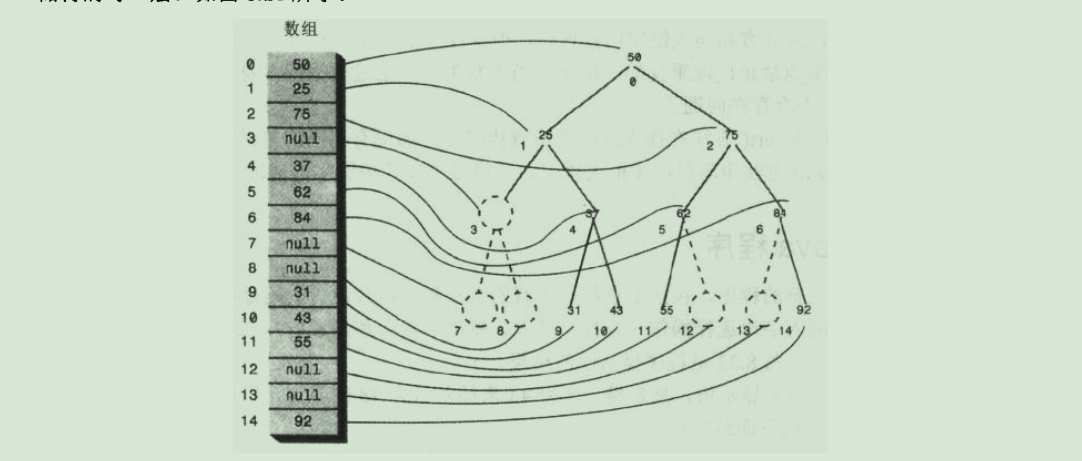
9.重复关键字
由于二叉搜索树的特性是:右子节点的key值大于等于父节点,所以在insert操作中,关键字key值相同的节点插入到与它相同的节点的右子节点处。在查询操作时,获取到的是多个相同节点的第一个节点。
注:以上图片摘自《Java数据结构和算法》这本书