数据结构中的查找算法总结

静态查找是数据集合稳定不需要添加删除元素的查找包括：

1. 顺序查找
2. 折半查找
3. Fibonacci
4. 分块查找

 静态查找可以用线性表结构组织数据，这样可以使用顺序查找算法，再对关键字进行排序就可以使用折半查找或斐波那契查找等算法提高查找效率，平均查找长度：折半查找最小，分块次之，顺序查找最大。顺序查找对有序无序表均适用，折半查找适用于有序表，分块查找要求表中元素是块与块之间的记录按关键字有序

动态查找是数据集合需要添加删除元素的查找包括：
　　1. 二叉排序树
　　2. 平衡二叉树

　　3. 散列表

1. 顺序查找

　　顺序查找适合于存储结构为顺序存储或链接存储的线性表。

　　顺序查找属于无序查找算法。从数据结构线形表的一端开始，顺序扫描，依次将扫描到的结点关键字与给定值k相比较，若相等则表示查找成功

　　　

　　查找成功时的平均查找长度为： ASL = 1/n(1+2+3+…+n) = (n+1)/2 ;
　　

　　顺序查找的时间复杂度为O(n)。

2. 二分查找

　　元素必须是有序的，如果是无序的则要先进行排序操作。

　　二分查找即折半查找，属于有序查找算法。用给定值value与中间结点mid的关键字比较，若相等则查找成功；若不相等，再根据value与该中间结点关键字的比较结果确定下一步查找的子表

　　将数组的查找过程绘制成一棵二叉树排序树，如果查找的关键字不是中间记录的话，折半查找等于是把静态有序查找表分成了两棵子树，即查找结果只需要找其中的一半数据记录即可，等于工作量少了一半，然后继续折半查找，效率高。

　　根据二叉树的性质，具有n个结点的完全二叉树的深度为[log₂n]+1。尽管折半查找判定二叉树并不是完全二叉树，但同样相同的推导可以得出，最坏情况是查找到关键字或查找失败的次数为[log₂n]+1，最好的情况是1次。

　　时间复杂度为O(log₂n)；

 　　折半计算mid的公式

　　　　mid = (low+high)/2;
        if(a[mid]==value)
            return mid;
        if(a[mid]>value)
            high = mid-1;
        if(a[mid]<value)
            low = mid+1;

 

 

　　折半查找判定数中的结点都是查找成功的情况，将每个结点的空指针指向一个实际上不存在的结点——外结点，所有外界点都是查找不成功的情况，如图所示。如果有序表的长度为n,则外结点一定有n+1个

折半查找判定数中，某结点所在的层数就是即将要比较的次数，整个判定树代表的有序表的平均查找长度即为查找每个结点的比较次数之和除以有序表的 长度。

  例如：长度为10的有序表的平均查找长度为

        ASL=(1*1+2*2+3*4+4*3)/10=29/10;

 

折半查找判定数中，查找不成功的次数即为查找相应外结点与内结点的比较次数。整个判定树代表的有序表的平均查找长度。查找失败时的有序表的平均查找长度即为查找每个外结点的比较次数之和除以外结点的个数。

   例如：查找失败时长度为10的有序表的平均查找长度为

 ASL=(3*5+4*6)/11=39/11;

 

3. 插值查找

　　改进二分查找算法，将查找点的选择改进为自适应选择，差值查找也属于有序查找。　

　　对于表长较大，而关键字分布又比较均匀的查找表来说，插值查找算法的平均性能比折半查找要好的多。反之，数组中如果分布非常不均匀，那么插值查找未必是很合适的选择。

　　折半计算mid的公式，等式变换后得到: mid = (low+high)/2 = low + (high-low)/2

　　 mid等于最低下标low加上最高下标high与low的差的一半。将这个 1/2 进行改进，通过类比，改进为下面的计算方案:

　　mid = low + ((key - a[low])/(a[high] - a[low]))(high - low)这样就可以大大提高查找的效率。

　　时间复杂度均为O(log₂n)。

 

4. 斐波那契查找

　　改进二分查找算法，通过运用黄金比例选择查找点进行查找，同样地，斐波那契查找也属于一种有序查找算法。

　　斐波那契查找的时间复杂也为O(logn)，但就平均性能来说，斐波那契查找要优于折半查找。可惜如果是最坏情况，比如这里key=l，那么始终都处于左侧长半区在查找，则查找效率要低于折半查找。

　　复杂度也为O(log₂n)

5. 分块查找

分块查找的平均查找长度ASL是折半查找的平均查找长度加顺序查找块内平均查找长度

6. 树表查找

　　如果查找的数据集是有序线性表，并且是顺序存储的，查找可以用折半、插值、斐波那契等查找算法来实现，可惜，因为有序，在插入和删除操作上，就需要耗费大量的时间
　　若查找表无序，则插入删除可无需移动大量记录，但于查找不利。有没有一种即可以使得插入和删除效率不错，又可以比较高效率地实现查找的算法呢?

　　我们把这种需要在查找时插入或删除的查找表称为动态查找表。动态查找不像是“查找”，更像是一个对表进行“创建、扩充、修改、删除”的过程。

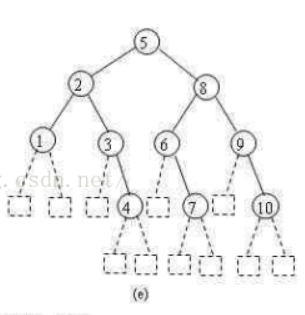
　　二叉排序树(Binary Sort Tree)，又称为二叉查找树。它或者是一棵空树，或者是具有下列性质的二叉树。
　　　 若它的左子树不空，则左子树上所有结点的值均小于它的根结点的值;
　　　 若它的右子树不空 ，则右子树上所有结点的值均大于它的根结点的值;
　 　　它的左、右子树也分别为二叉排序树。

　   平衡二叉树(AVL树)

　　    平衡二叉树，是一种二叉排序树，其中每一个节点的左子树和右子树的高度差至多等于1。

　　    从平衡二叉的英文名字(AVL树)，你也可以体会到，它是一种高度平衡的二叉排序树。

　　    高度平衡意思是说，要么它是一棵空树，要么它的左子树和右子树都是平衡二叉树，且左子树和右子树的深度之差的绝对值不超过1。

　　多路查找树

　　我们之前谈的树，都是一个结点可以有多个孩子，但是它自身只存储一个元素。二叉树限制更多，结点最多只能有两个孩子。
　　一个结点只能存储一个元素，在元素非常多的时候，就使得要么树的度非常大(结点拥有子树的个数的最大值)，要么树的高度非常大，甚至两者都必须足够大才行。这就使得内存存取外存次数非常多，这显然成了时间效率上的瓶颈，这迫使我们要打破每一个结点只存储一个元素的限制 ，为此引入了多路查找树的概念。

　　多路查找树，其每一个结点的孩子数可以多于两个，且每一个结点处可以存储多个元素。由于它是查找树，所有元素之间存在某种特定的排序关系。
在这里，每一个结点可以存储多少个元素，以及它的孩子数的多少是非常关键的。它的4种特殊形式 : 2-3 树、2-3-4 树、B 树和B+树。

 

7. 哈希查找