周博磊老师强化学习纲领笔记第二课：MDP，Policy Iteration与Value Iteration

gym环境：FrozenLake-v0：http://gym.openai.com/envs/FrozenLake-v0/

代码来自：周博磊老师的GitHub：https://github.com/cuhkrlcourse/RLexample/tree/master/MDP

环境如下：

SFFF       (S: starting point, safe)
FHFH       (F: frozen surface, safe)
FFFH       (H: hole, fall to your doom)
HFFG       (G: goal, where the frisbee is located)

• 环境解释：冰封湖问题，智能体控制角色在网格世界中的移动。网格中的某些冰面是可行走的，而某些冰面会导致主体掉入水中。另外，智能体的移动方向是不确定的，并且仅部分取决于所选方向。（也就是如果你想向上走，你选择的动作是向上走，但是实际不一定向上走，可能会发生偏移，向左，或向右，三个方向的概率是等价的，也就是都是0.3333）代理商因找到通往目标砖的可步行路径而获得奖励。

# env.nA, 表示每个可以选择的动作的个数为4，动作空间
# env.nS, 表示状态的总数为16，状态空间
# env.P[state][a], 表示在状态state下执行动作a，返回的是prob概率， next_state下一个状态，reward奖励, done是否结束

Policy Iteration：

• 目标：寻找一个最后策略：(pi)

• 解决方法：不断的迭代Bellman expectation backup（下面的公式5）

• Policy Iteration algorithm:

  At each iteration t+1

  update (v_{t+1}(s)) from (v_t(s')) for all states (s in S) where (s') is a successor states of s

   (v_{t+1}(s)=sum_{a in A}pi(a|s)[R(s,a)+gammasum_{s'in S}P(s'|s,a)v_t(s')])

  Convergence: (v_1 o v_2 o ... o v^pi)

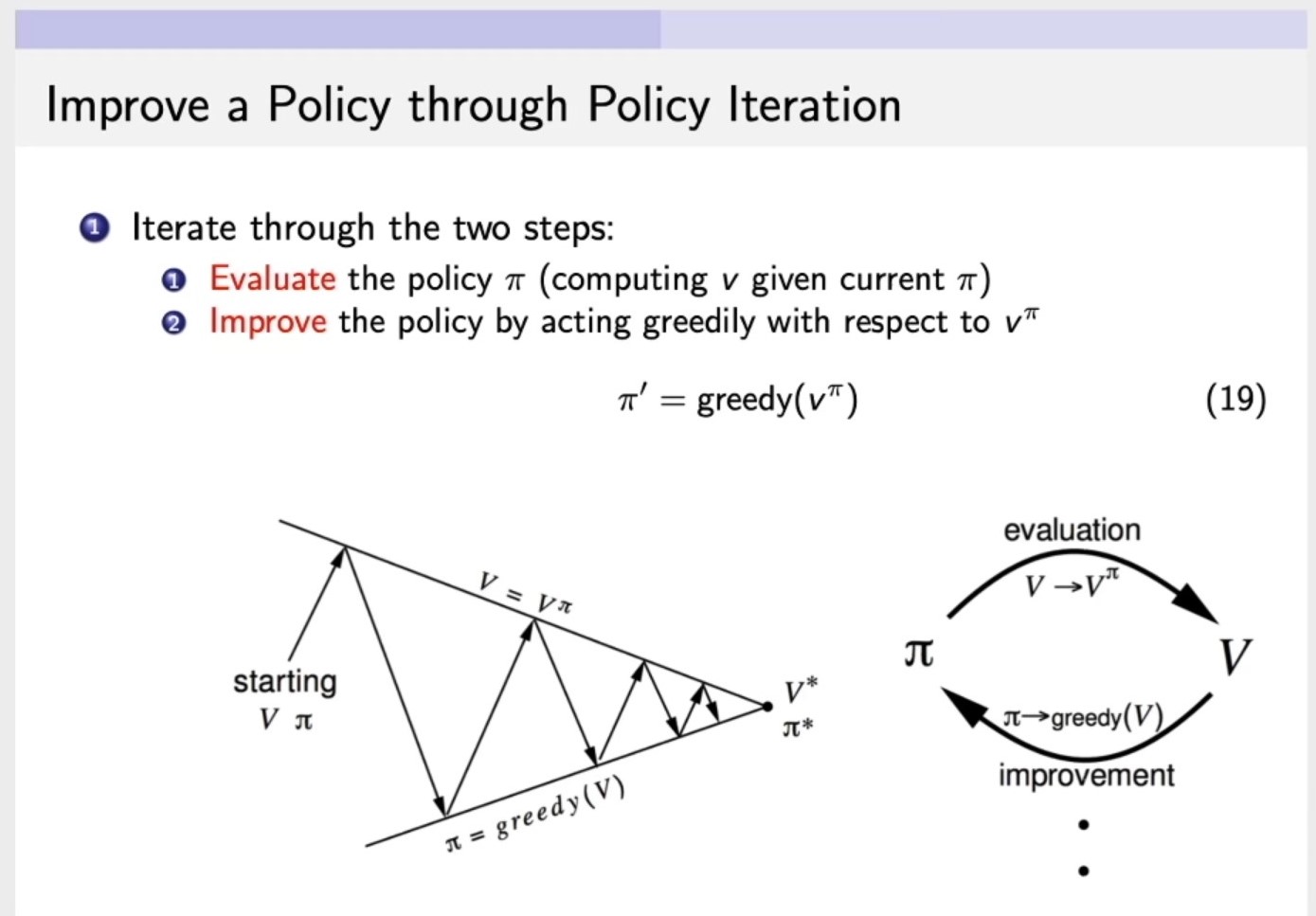
• Iterate through the two steps:

  • Evaluate the policy (pi) (computing (v) given current (pi))，第一步：计算v函数，输入，环境，策略以及衰减因子，来计算这个策略的价值。
  • Improve the policy by acting greedily wirh respect to (v^pi)，第二步：改进策略policy，通过对 (v^pi) （第一步通过(pi)求解出来的(v)）采取贪心的算法，来改进策略policy。

Policy Iteration：

"""
Solving FrozenLake environment using Policy-Iteration.
Adapted by Bolei Zhou for IERG6130. Originally from Moustafa Alzantot (malzantot@ucla.edu)
"""
import numpy as np
import gym

RENDER=False
GAMMA=1.0

# 计算策略policy跑一个回合的奖励：输入环境，策略以及衰减因子，跑一个回合，返回奖励值
def run_episode(env, policy, gamma = GAMMA, render = False):
    """ Runs an episode and return the total reward """
    obs = env.reset()
    # 重置环境
    total_reward = 0
    step_idx = 0
    while True:
        if render:
            env.render()
        # 如果想看环境渲染的话，就设置输入的render为True，render默认为False
        obs, reward, done , _ = env.step(int(policy[obs]))
        total_reward += (gamma ** step_idx * reward)
        step_idx += 1
        if done:
            break
    return total_reward,step_idx

# 计算策略policy的平均奖励
def evaluate_policy(env, policy, gamma = GAMMA, n = 100):
    scores = [run_episode(env, policy, gamma, render=RENDER) for _ in range(n)]
    return np.mean(scores)

# 第一步：计算v函数，输入，环境，策略以及衰减因子，来计算这个策略的价值
def compute_policy_v(env, policy, gamma=GAMMA):
    """ Iteratively evaluate the value-function under policy.
    Alternatively, we could formulate a set of linear equations in iterms of v[s]
    and solve them to find the value function.
    """
    v = np.zeros(env.env.nS)
    eps = 1e-10
    # 将精度收敛到eps的时候，就停止更新
    while True:
        prev_v = np.copy(v)
        for s in range(env.env.nS):
            policy_a = policy[s]
            v[s] = sum([p * (r + gamma * prev_v[s_]) for p, s_, r, _ in env.env.P[s][policy_a]])
        if (np.sum((np.fabs(prev_v - v))) <= eps):
            # value converged
            break
    return v

# 第二步：改进策略policy，通过对old_policy_v采取贪心的算法，来改进策略policy
def extract_policy(v, gamma = GAMMA):
    """ Extract the policy given a value-function """
    policy = np.zeros(env.env.nS)
    for s in range(env.env.nS):
        q_sa = np.zeros(env.env.nA)
        for a in range(env.env.nA):
            q_sa[a] = sum([p * (r + gamma * v[s_]) for p, s_, r, _ in  env.env.P[s][a]])
        policy[s] = np.argmax(q_sa)

    return policy

# policy_iteration的主要算法
def policy_iteration(env, gamma = GAMMA):
    """ Policy-Iteration algorithm """
    policy = np.random.choice(env.env.nA, size=(env.env.nS))  # initialize a random policy

    max_iterations = 200000
    gamma = GAMMA
    for i in range(max_iterations):
        old_policy_v = compute_policy_v(env, policy, gamma)
        # 第一步：计算v函数，输入，环境，策略以及衰减因子，来计算这个策略的价值
        new_policy = extract_policy(old_policy_v, gamma)
        # 第二步：改进策略policy，通过对old_policy_v采取贪心的算法，来改进策略policy
        if (np.all(policy == new_policy)):
            # 如果policy已经不在发生改变了，也就是收敛了，无法提升了
            print ('Policy-Iteration converged at step %d.' %(i+1))
            break
        policy = new_policy
    return policy

if __name__ == '__main__':
    env_name  = 'FrozenLake-v0' # 'FrozenLake4x4-v0'
    env = gym.make(env_name)

    optimal_policy = policy_iteration(env, gamma = GAMMA)
    scores = evaluate_policy(env, optimal_policy, gamma = GAMMA)
    print('Average scores = ', np.mean(scores))

    print(optimal_policy)
    total,step=run_episode(env,optimal_policy,GAMMA,True)
    print("一共走了：",step)

Value Iteration：

• 目标：寻找一个最后策略：(pi)

• 解决方法：不断的迭代Bellman optimality backup（下面的公式5）

• Value Iteration algorithm:

  initialize (k =1) and (v_0(s)=0) for all states (s)

  For (k=1) : (H)

  ​ for each state (s)

  ​  (q_{k+1}(s,a)=R(s,a)+gammasum_{s' in S}P(s'|s,a)v_k(s'))

  ​  (v_{k+1}(s)=max_aq_{k+1}(s,a))

  ​ (k leftarrow k+1)

  To retrieve the optimal policy after the value iteration:

   (pi(s)=argmax_a[R(s,a)+gammasum_{s' in S}P(s'|s,a)v_{k+1}(s')])

Value Iteration：

"""
Solving FrozenLake environment using Value-Itertion.
Updated 17 Aug 2020
"""
import numpy as np
import gym
from gym import wrappers
from gym.envs.registration import register

def run_episode(env, policy, gamma = 1.0, render = False):
    """ Evaluates policy by using it to run an episode and finding its
    total reward.
    args:
    env: gym environment.
    policy: the policy to be used.
    gamma: discount factor.
    render: boolean to turn rendering on/off.
    returns:
    total reward: real value of the total reward recieved by agent under policy.
    """
    obs = env.reset()
    total_reward = 0
    step_idx = 0
    while True:
        if render:
            env.render()
        obs, reward, done , _ = env.step(int(policy[obs]))
        total_reward += (gamma ** step_idx * reward)
        step_idx += 1
        if done:
            break
    return total_reward


def evaluate_policy(env, policy, gamma = 1.0,  n = 100):
    """ Evaluates a policy by running it n times.
    returns:
    average total reward
    """
    scores = [
            run_episode(env, policy, gamma = gamma, render = False)
            for _ in range(n)]
    return np.mean(scores)

def extract_policy(v, gamma = 1.0):
    """ Extract the policy given a value-function """
    policy = np.zeros(env.env.nS)
    for s in range(env.env.nS):
        q_sa = np.zeros(env.action_space.n)
        for a in range(env.action_space.n):
            for next_sr in env.env.P[s][a]:
                # next_sr is a tuple of (probability, next state, reward, done)
                p, s_, r, _ = next_sr
                q_sa[a] += (p * (r + gamma * v[s_]))
        policy[s] = np.argmax(q_sa)
    return policy


def value_iteration(env, gamma = 1.0):
    """ Value-iteration algorithm """
    v = np.zeros(env.env.nS)  # initialize value-function
    max_iterations = 100000
    eps = 1e-20
    for i in range(max_iterations):
        prev_v = np.copy(v)
        q_sa=np.zeros(env.env.nA)
        for s in range(env.env.nS):
            for a in range(env.env.nA):
                q_sa[a] = sum([p*(r + gamma * prev_v[s_]) for p, s_, r, _ in env.env.P[s][a]])
            v[s] = max(q_sa)
        if (np.sum(np.fabs(prev_v - v)) <= eps):
            print ('Value-iteration converged at iteration# %d.' %(i+1))
            break
    return v


if __name__ == '__main__':

    env_name  = 'FrozenLake-v0' # 'FrozenLake4x4-v0'
    env = gym.make(env_name)
    gamma = 1.0
    optimal_v = value_iteration(env, gamma);
    policy = extract_policy(optimal_v, gamma)
    policy_score = evaluate_policy(env, policy, gamma, n=1000)
    print('Policy average score = ', policy_score)
    print(policy)

Policy Iteration和Value Iteration的区别：

①：Policy iteration主要包括两部分：policy evaluation+policy improvement，这两部分反复迭代，直到收敛。初始化一个策略policy，对策略policy进行价值评估，然后再根据价值，重新制定最优策略，反复迭代。

②：Value iteration主要包括两部分：finding optimal value function+one policy extraction，寻找一个最优的价值函数，然后根据价值函数，指定最优的策略，因为价值函数是最优的，所以策略也是最优的。

③：策略迭代的收敛速度更快一些，在状态空间较小时，最好选用策略迭代方法。当状态空间较大时，值迭代的计算量更小一些。

Problem	Bellman Equation	Algorithm
Prediction	Bellman Expectation Equation	Iterative Policy Evaluation
Control	Bellman Expectation Equation	Policy Iteration
Control	Bellman Optimality Equation	Value Iteration

Bellman expectation Equation：（当前状态跟未来状态的一个关联，(G_t)展开的首项是(R_{t+1})）

[v^pi(s)=E_pi[R_{t+1}+gamma v^pi(s_{t+1})|s_t=s] ag 1 ]

[q^{pi}(s,a)=E_pi[R_{t+1}+gamma q^pi(s_{t+1},A_{t+1})|s_t=s,A_t=a] ag 2 ]

（3）式和（4）式象征着价值函数和q函数之间的关联

[v^pi(s)=sum_{a in A}pi(a|s)q^pi(s,a) ag 3 ]

[q^pi(s,a)=R_s^a+gamma sum_{s'in S}P(s'|s,a)v^pi(s') ag 4 ]

（4）式带入到（3）式中得到（象征着当前状态的价值与未来状态的价值之间的一个关联）

[v^pi(s)=sum_{a in A}pi(a|s)[R(s,a)+gamma sum_{s'in S}P(s'|s,a)v^pi(s')] ag 5 ]

（3）式带入到（4）式中得到（象征着当前时刻的q函数与未来时刻的q函数之间的一个关联）：

[q^pi(s,a)=R(s,a)+gamma sum_{s'in S}P(s'|s,a)sum_{a' in A}pi(a'|s')q^pi(s',a') ag 6 ]

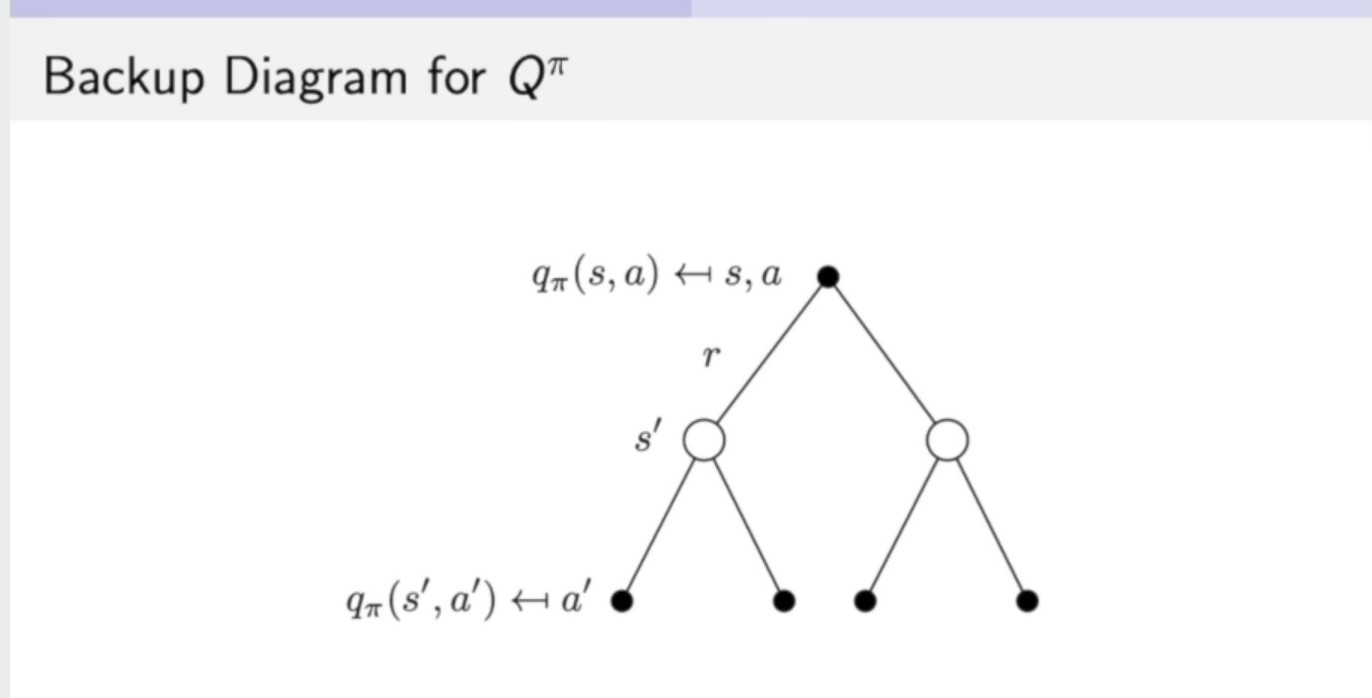
公式（5）进行backup后得到Bellman expectation backup：

[v_{t+1}(s)=sum_{a in A}pi(a|s)[R(s,a)+gamma sum_{s' in S}P(s'|s,a)v_t(s')] ag 7 ]

上式转换成马尔可夫奖励过程的形式：

[v_{t+1}(s)=R^pi(s)+gamma P^pi(s'|s)v_t(s') ag 8 ]

Bellman Optimality Equation：

[v^pi(s)=max_{a in A}q^pi(s,a) ag 9 ]

[q^*(s,a)=R(s,a)+gamma sum_{s'in S}P(s'|s,a)v^*(s') ag {10} ]

（10）式带入到（9）式得到：

[v^*(s)=max_aR(s,a)+gamma sum_{s'in S}P(s'|s,a)v^*(s') ag {11} ]

（9）式带入到（10）式得到：

[q^*(s,a)=R(s,a)+gamma sum_{s'in S}P(s'|s,a)max_a'q^*(s',a') ag {12} ]

公式(4)进行backup后得到 Bellman Optimality backup：

[v(s)=max_{ain A}[R(s,a)+gamma sum_{s'in S}P(s'|s,a)v(s')] ag {13} ]