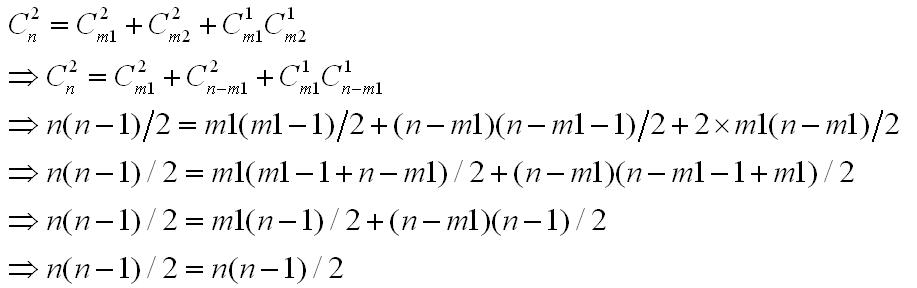算法导论逆序对（修改合并排序）

题目：给出一个算法，它能用O（n lgn）的最坏情况运行时间，确定n个不同元素的任何排列中逆序对的数目。

答：解决这个问题的核心问题是一个排列的逆序对数等于分解的二个排列的逆序对数和二个排列之间的逆序对数之和。

即：将一个个数为n的排列分解为个数为m1和m2二个排列，证明 

接着就是利用递归算法的从底层向上运算的特性逐层求解各层的逆序对数。

问题化简成如何求解二个有序排列的逆序对数了；

设：将A排列分解成B和C二个有序排列；i为B中的数，j为C中数；在合并排序时，i<j则将j放回A中；也就是说看设C中已有b个数放入A中；针对i有b个逆序对；最后将B中所有数的逆序对数相加，即可求出二个排列之间的逆序对数。

代码：

#include "iostream"
#define n 100
#define max 0x7fffffff
using namespace std;

int A[n],B[n],C[n];

void display(int n1){
    int i;
    for(i=1;i<=n1;i++)
        cout<<A[i]<<" ";
    cout<<endl;
}

int paixu(int p,int r,int q){
    int sum=0;
    int i,j,k;
    int m2;
    for(i=1;i<=r-p+1;i++)
        B[i]=A[i+p-1];
    for(i=1;i<=q-r;i++)
        C[i]=A[i+r];
    B[r-p+2]=max;
    C[q-p+1]=max;
    i=j=1;
    m2=0;
    for(k=p;k<=q;k++){
        if(B[i]>C[j]){
            A[k]=C[j];
            j++;    
            m2++;
        }
        else {
            A[k]=B[i];
            i++;
            sum+=m2;
        }
    }
    return sum;
}

int mergeSort(int p,int q){
    if(q>p){
        int r=(p+q)/2;
        int m1=mergeSort(p,r);
        int m2=mergeSort(r+1,q);
        return paixu(p,r,q)+m1+m2;
    }
    else return 0;
} 

void main(){
cout<<"请输入一组不相同的数据（以0结束）："<<endl;
int a,i=1;
cin>>a;
while(a!=0){
    A[i]=a;
    i++;
    cin>>a;
}//输入一组不相同的数据
cout<<"逆序对数目："<<mergeSort(1,i-1)<<endl;
display(i-1);
getchar();
getchar();
}