什么是算法
算法(Algorithm):一个计算过程,解决问题的方法
一个算法应该具有以下七个重要的特征:
①有穷性(Finiteness):算法的有穷性是指算法必须能在执行有限个步骤之后终止; ②确切性(Definiteness):算法的每一步骤必须有确切的定义; ③输入项(Input):一个算法有0个或多个输入,以刻画运算对象的初始情况,所谓0个输入是指算法本身定出了初始条件; ④输出项(Output):一个算法有一个或多个输出,以反映对输入数据加工后的结果。没有输出的算法是毫无意义的; ⑤可行性(Effectiveness):算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步,即每个计算步都可以在有限时间内完成(也称之为有效性); ⑥高效性(High efficiency):执行速度快,占用资源少; ⑦健壮性(Robustness):对数据响应正确。
时间复杂度
时间复杂度举例说明
时间复杂度:就是用来评估算法运行时间的一个式子(单位)。一般来说,时间复杂度高的算法比复杂度低的算法慢
类比生活中的一些时间,估计时间
print('hello world')
print('hello python')
print('hrllo ssd ') #O(1) 大O,简而言之可以认为它的含义是“order of”(大约是)。
#
for i in range(n):
print('hello world')
for j in range(n):
print('hello world') #O(n^2)
for i in range(n):
for j in range(i):
print('hrllo owd') ##O(n^2)
n= 64
while n>1:
print(n) #O(log2n)或者O(logn)
n = n//2
while的分析思路: # 假如n = 64的时候会输出:如下图

这时候可以发现规律:

常见的算法时间复杂度(按照效率)
由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<O(n2logn)< Ο(n3)<…<Ο(2^n)<Ο(n!)
例如:

由图中我们可以看出,当 n 趋于无穷大时, O(nlogn) 的性能显然要比 O(n^2) 来的高
一般来说,只要算法中不存在循环语句,其时间复杂度就是 O(1)
而时间复杂度又分为三种:
- 最优时间复杂度 (Best-Case)
- 平均时间复杂度 (Average-Case)
- 最差时间复杂度 (Worst-Case)
对于最优时间复杂度,其价值不大,因为它没有提供什么有用信息,其反映的只是最乐观最理想的情况,没有参考价值。对于最坏时间复杂度,提供了一种保证,表明算法在此种程度的基本操作中一定能完成工作。对于平均时间复杂度,是对算法的一个全面评价,因此它完整全面的反映了这个算法的性质。但另一方面,这种衡量并没有保证,不是每个计算都能在这个基本操作内完成。而且,对于平均情况的计算,也会因为应用算法的实例分布可能并不均匀而难以计算。因此,我们主要关注算法的最坏情况,亦即最坏时间复杂度。
时间复杂度的几条基本计算规则
1.基本操作,即只有常数项,认为其时间复杂度为O(1) 2.顺序结构,时间复杂度按加法进行计算 3.循环结构,时间复杂度按乘法进行计算 4.分支结构,时间复杂度取最大值 5.判断一个算法的效率时,往往只需要关注操作数量的最高次项,其它次要项和常数可以忽略 6.在没有特殊说明时,我们所分析的算法的时间复杂度都是指最坏时间复杂度
如何一眼判断时间复杂度
- 循环减半的过程-》O(logn)
- 几次循环就是n的几次方的复杂度
空间复杂度
空间复杂度:用来评估算法内存占用大小的一个式子
数据结构
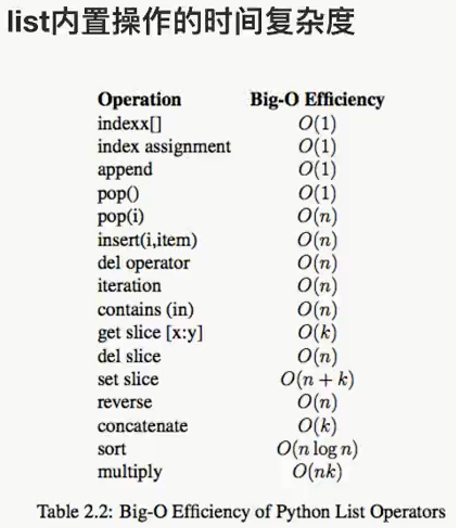
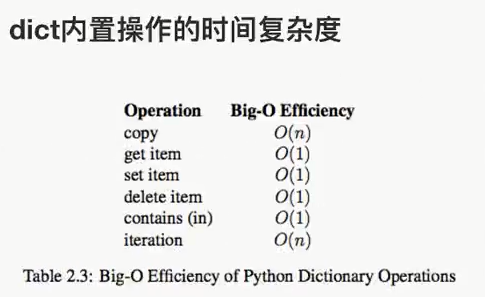
我们如何用Pthon中的类型来保存一个班的学生信息?如果想要快速的通过学生姓名获取其信息呢? 实际上当我们在思考这个问题的时候,我们已经用到了数据结构。列表和字典都可以存储一个班的学生信息,但是想要在列表中获取一名同学的信息时,就要遍历这个列表,其时间复杂度为O(n),而使用字典存储时,可将学生姓名作为字典的键,学生信息作为值,进而查询时不需要遍历便可快速获取到学生信息,其时间复杂度为0(1)。 我们为了解决问题,需要将数据保存下来,然后根据数据的存储方式来设计算法实现进行处理,那么数据的存储方式不同就会导致需要不同的算法进行处理。我们希望算法解决问题的效率越快越好,于是我们就需要考虑数据究竟如何保存的问题,这就是数据结构。在上面的问题中我们可以选Python中的列表或字典来存储学生信息。列表和字典就是Python内建帮我们封装好的两种数据结构。
概念
数据是一个抽象的概念,将其进行分类后得到程序设计语言中的基本类型。如:int,float,char等。数据元素之间不是独立的,存在特定的关系,这些关系便是结构。数据结构指数据对象中数据元素之间的关系。 Python给我们提供了很多现成的数据结构类型,这些系统自己定义好的,不需要我们自己去定义的数据结构叫做Python的内置数据结构,比如列表、元组、字典。而有些数据组织方式,Python系统里面没有直接定义,需要我们自己去定义实现这些数据的组织方式,这些数据组织方式称之为Python的扩展数据结构,比如栈,队列等。
算法与数据结构的区别
数据结构只是静态的描述了数据元素之间的关系。 高效的程序需要在数据结构的基础上设计和选择算法。 程序=数据结构+算法 总结:算法是为了解决实际问题而设计的,数据结构是算法需要处理的问题载体
抽象数据类型(Abstract Data Type)
抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起,进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开,使它们相互独立。 最常用的数据运算有五种: ·插入 ·删除 ·修改 ·查找 ·排序
Python内置类型性能分析
timeit模块
timeit模块可以用来测试一小段Python代码的执行速度
class timeit.Timer(stmt='pass',setup='pass',timer=<timer function>)
Timer是测量小陕代码执行速度的类。
stmt参数是要测试的代码语句(statment);
setup参数是运行代码时需要的设置;
timer参数是一个定时器函数,与平台有关。
timeit.Timer.timeit(number=1000000)
Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数,默认为1000000次。方法
返回执行代码的平均耗时,一个float类型的秒数。
实例
from timeit import Timer
def func():
for i in range(100):
for q in range(100+i):
print("过了好长时间")
timer=Timer("func()","from __main__ import func")
print(timer.timeit(10))
'''
...
过了好长时间
过了好长时间
1.207258653788079
'''
对于递归的简单复习
递归最大的两个特点:
- 调用自身
- 结束条件
做个小练习来判断一下下面那些函数是递归函数?


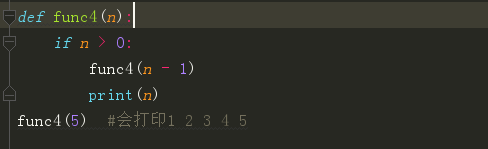
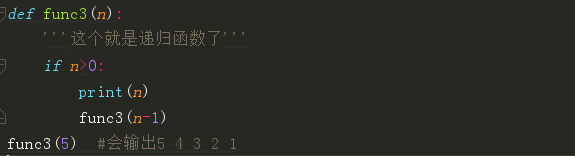
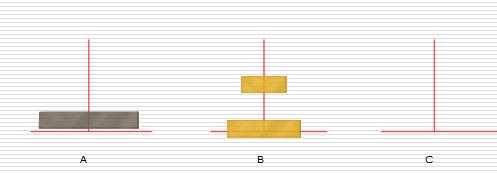
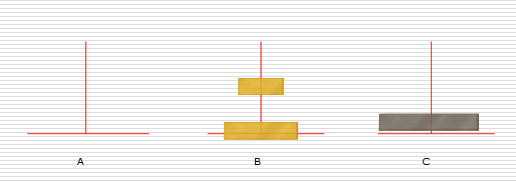
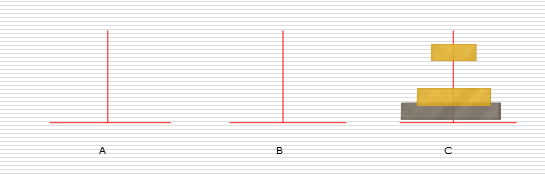
递归练习:汉诺塔问题
解决思路:
假设有n个盘子:
- 1.把n-1个圆盘从A经过C移动到B
- 2.把第n个圆盘从A移动到C
- 3.把n-1个小圆盘从B经过A移动到C

代码实现
def func(n,a,b,c):
if n==1:
print(a,'-->',c)
else:
func(n-1,a,c,b) #将n-1个盘子从a经过c移动到b
print(a,'-->',c) #将剩余的最后一个盘子从a移动到c
func(n-1,b,a,c) #将n-1个盘子从b经过a移动到c
n = int(input('请输入汉诺塔的层数:'))
func(n,'柱子A','柱子B','柱子C')
总结:汉诺塔移动次数的递推式:h(x)=2h(x-1)+1