题目信息
题目来源:CCF NOIP2015 提高组 D1T2;
在线评测地址:Luogu#2661,LOJ#2421;
运行限制:(1.00 extrm{ms}/128 extrm{MiB})
题目描述
有 (n) 个同学(编号为 (1) 到 (n))正在玩一个信息传递的游戏。在游戏里,每人都有一个固定的信息传递对象。其中,编号为 (i) 的同学的信息传递对象是编号为 (T_i) 的同学。
游戏开始时,每人都只知道自己的生日。之后每一轮中,所有人会同时将自己当前所知的生日信息告诉各自的信息传递对象(注意:可能有人可以从若干人那里获取信息, 但是每人只会把信息告诉一个人,即自己的信息传递对象)。当有人从别人口中得知自己的生日时,游戏结束。请问该游戏一共可以进行几轮?
输入格式
输入数据第一行包含一个正整数 (n) 表示人数;
第二行包含 (n) 个用空格隔开的正整数 (T_1,T_2,cdots,T_n),其中第 (i) 个整数 (T_i) 表示编号为 (i) 的同学的信息传递对象是编号为 (T_i) 的同学。
输出格式
输出一行,表示游戏最多可以进行几轮。
数据规模和约定
- 对于 (30\%) 的数据,(nle 200);
- 对于 (60\%) 的数据,(nle 2500);
- 对于 (100\%) 的数据,(1le nle 2 imes 10^5)。
保证 (1le T_ile n),(T_i eq i)。
分析
给定一张每个节点出度均为 (1) 的有向图,求最小环大小。
根据定义,可知这张图是内向树森林(不就是基环树吗何必那么高大上)。我们只需要找每一棵树的环就可以了。
找环可以用 DFS,但是这种做法效率比较低(万一没有开无限栈就是直接爆炸了),可以考虑直接遍历。记录一个时间戳,重复搜到了就用当前时间减去时间戳记录下的时间更新答案即可。
举个栗子:(红色箭头表示搜到的节点)
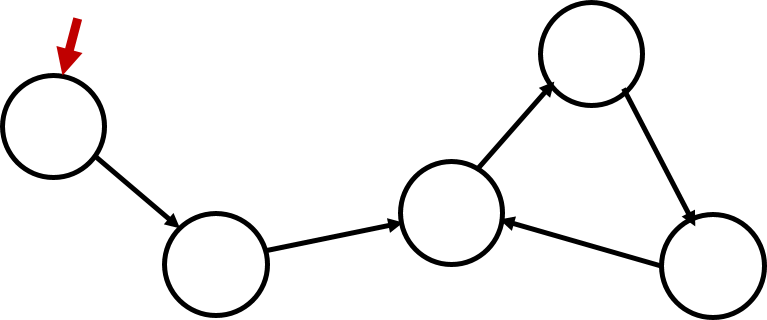
标记完成所有的时间戳后:
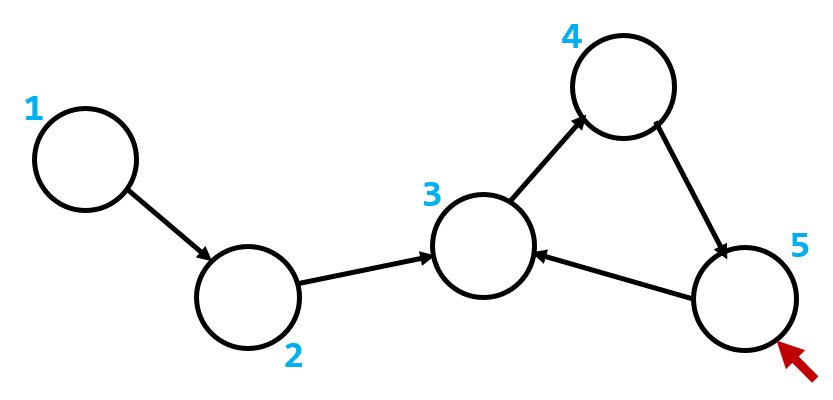
继续搜,发现已经标记:
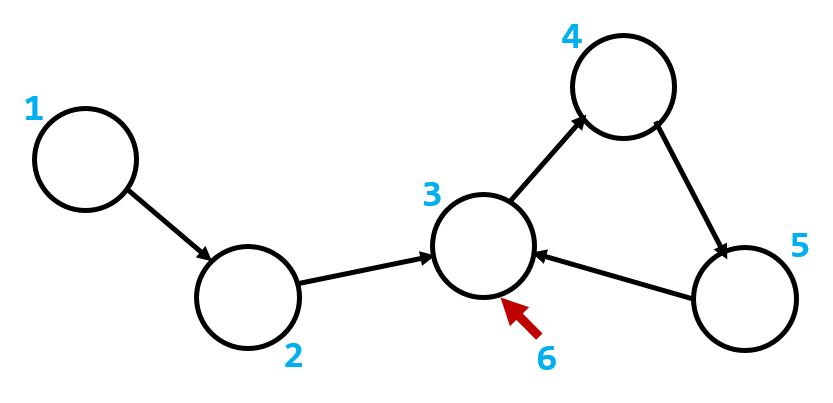
(6-3=3),这就是环的大小。
注意事项
- 每一次搜索一定要记录下初始时间。如果搜到初始时间之前的节点就是环已经更新过了;
- 初始时间可能等于重复节点,即只有一个环的情况。
Code
#include <cstdio>
#include <cctype>
using namespace std;
const int max_n = 200000;
int a[max_n], dep[max_n];
#define gc getchar
inline int read()
{
int c = gc(), t = 1, n = 0;
while (isspace(c)) { c = gc(); }
if (c == '-') { t = -1, c = gc(); }
while (isdigit(c)) { n = n * 10 + c - '0', c = gc(); }
return n * t;
}
int main()
{
int n = read(), tmp = 1, ptr, ans = max_n, sta;
for (int i = 0; i < n; i++)
a[i] = read() - 1;
for (int i = 0; i < n; i++)
if (!dep[i])
{
sta = tmp, dep[i] = tmp++, ptr = a[i];
while (!dep[ptr])
{
dep[ptr] = tmp++;
ptr = a[ptr];
}
if (dep[ptr] >= sta && ans > tmp - dep[ptr])
ans = tmp - dep[ptr];
}
printf("%d
", ans);
return 0;
}