Floyd算法

费洛伊德算法，用于解决任意两点的间最短路的问题，同时也被用于计算有向图的传递闭包。Floyd的时间复杂度为O(n^{^3}),空间复杂度为O（n*n）。所以在运用此方法是，一定要考虑到时间的问题。

那么什么是Floyd算法呢？先来看一组代码。

void Floyd()
{
    for (int k = 1; k <= n; k++)
        for (int j = 1; j <= n; j++)
            for (int i = 1; i <= n; i++)
                per[i][j] = min(per[i][j], per[i][k]+per[k][j]);
}

最后的一行代码是不是看着很熟悉，没错。它的原理其实和Dijkstra最后的部分是相似的，比较这一驱节点和另一方向可达距离的大小，而后松弛操作（即更新）。只不过我们把松弛操作和不断移动驱前节点方到一起罢了。那它到底是如何实现的呢？

我们来看看这样一组图：

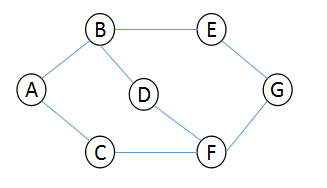
                               图一                                                                                   图二                                                                              图三                                                                          图四

 其实我们不断更新就是不断画三角的过程，在画三角的时候我们完成了对最短路径的处理。图一最初的状态没有遍历的，图二是已经执行了几步的：我们发现A到D的距离是MAX（无穷），所以不可能更新，它的最短距离A->B->D;图二：到C的距离显然为A->C;A->B->C的距离为MAX。我们执行几步又到F点，距离全为MAX无法更新，还是MAX；就这样它会将A->任意点的距离都更新一遍。然而这只是最外层的第一循环，还有n-1边的循环，那么这一遍的处理就可以看作为下一组做了松弛处理。

无论初始化还是查询和Dijkstra算法是一模一样的，大家可以自行去练练手了。